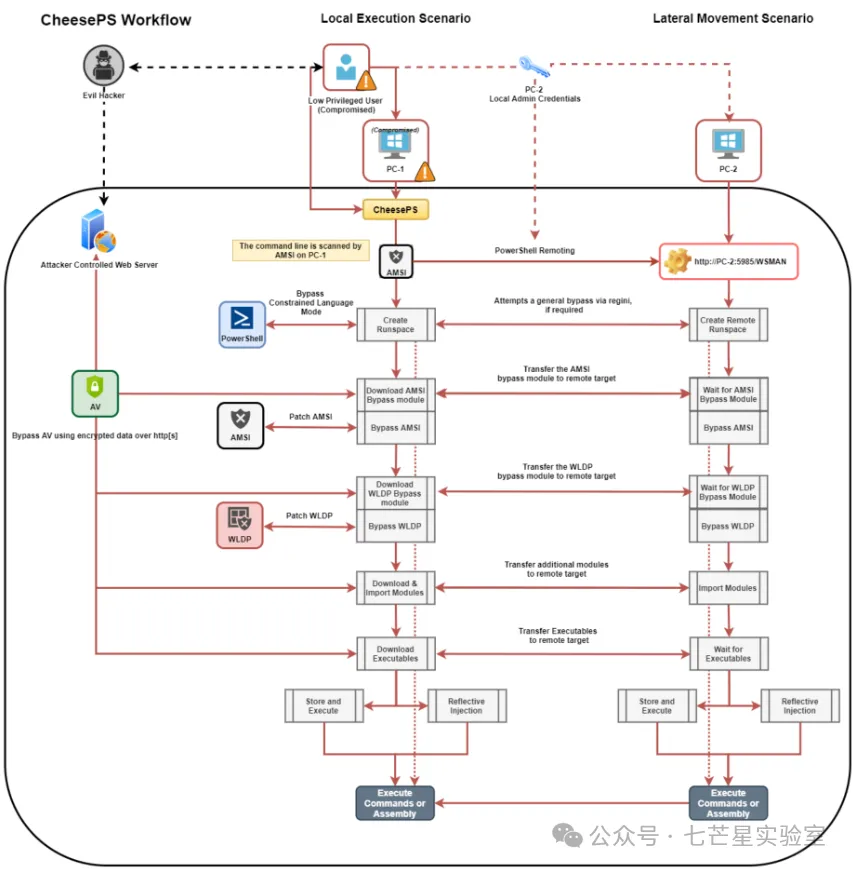
Density of subarrays
题目链接。
Problem
我们定义一个“\(c\) 序列”为序列里的数都是 \([1, c]\) 的序列。定义一个 \(c\) 序列的“密度”为最大的 \(p\),使得任意长度为 \(p\) 的序列(总共 \(c^p\) 个)都是它的子序列。
给定一个长度为 \(n\) 的“\(c\) 序列”,对 \(p \in [0, n]\),求该序列有多少个子序列的密度为 \(p\),答案对 \(998244353\) 取模。
数据范围:\(n, m \le 3000\)。
Sol
感觉这道题难点在于知道复杂度!如果这个题被扔到 OI 里,给两个部分分是不是就完全没难度了。
先考虑一下如何判定一个序列的密度。这是一个很简单的贪心。假如之前已经匹配到 \(i\),由于是任意长度为 \(p\) 的序列,所以肯定是尽量往后找。即找到第一个使得 \([i, j]\) 中出现 \(1 \sim c\) 所有数的位置 \(j\),然后让答案增加一,继续进行刚才的操作,无法再找到下一个 \(j\) 时结束。于是就有一个很简单的 DP:定义 \(f_{i, j}\) 表示填了 \(i\) 个数,密度为 \(j\) 的方案数。则有转移 \(f_{i, j} = \sum\limits_{k < i}f_{k, j - 1} \cdot w(k + 1, i)\),其中 \(w(l, r)\) 表示 \(a_l, a_{l + 1}, \dots, a_r\) 中有多少个子序列满足 \(1 \sim n\) 中的数都出现了至少一次。\(w(i, j)\) 是好算的,可以 \(\mathcal{O}(n^2)\) 预处理出。然后这就得到了一个很简单的 \(\mathcal{O}(n^3)\) 的做法。然后发现这道题 \(n \le 3000\) 还开了六秒,肯定就不是 \(\mathcal{O}(n^2)\) 的。仔细分析一下刚才做法的复杂度。不难发现,当 \(p > \frac nc\) 时,答案一定为 \(0\),所以刚才 DP 的第二维是 \(\mathcal{O}(\frac nc)\) 的,于是这个 DP 就变成了 \(\mathcal{O}(\frac{n^3}{c})\) 了。于是发现只有这个 \(c\) 比较小的时候才会跑的比较慢,想一下 \(c\) 比较小咋做。
不难得出一个暴力 DP:\(g_{i, j, S}\) 表示填了 \(i\) 个数,当前密度为 \(p\),\(1 \sim c\) 中的数填过的集合为 \(S\) 的方案数。转移是很简单的,枚举 \(a_i\) 选不选就行了。然后这个东西的时间复杂度是 \(\mathcal{O}(n\cdot \frac nc \cdot 2^c)\) 的。当 \(\frac{n^22^c}{c} = \frac{n^3}{c}\) 时,\(c = \log_2 n\)。所以 \(c\) 取 \(10\) 左右比较好。最后的时间复杂度变为 \(\mathcal{O}(\frac{n^3}{\log n})\)。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define fi first
#define se second
mt19937_64 eng(time(0) ^ clock());
template<typename T>
T rnd(T l, T r) { return eng() % (r - l + 1) + l; }
const int P = 998244353;
ll QPow(ll a, ll b) {ll res = 1;for (; b; a = a * a % P, b >>= 1)if (b & 1)res = res * a % P;return res;
}
int n, c;
int a[3005];
namespace SolveB {
int cnt, buc[3005];
ll g[3005][3005], h[3005], pw2[3005], ipw1[3005], ipw2[3005];
unsigned long long f[3005][3005];
void Work() {pw2[0] = 1;for (int i = 1; i <= n; i++)pw2[i] = pw2[i - 1] * 2 % P;for (int i = 0; i <= n; i++)ipw1[i] = QPow((pw2[i] + P - 1) % P, P - 2),ipw2[i] = QPow(pw2[i], P - 2);for (int l = 1; l <= n; l++) {memset(buc, 0, sizeof (buc));ll res = 1;for (int r = l; r <= n; r++) {if (buc[a[r]])res = res * ipw1[buc[a[r]]] % P;elsecnt++;buc[a[r]]++;res = res * (pw2[buc[a[r]]] + P - 1) % P;if (cnt == c)g[l][r] = res * ipw1[buc[a[r]]] % P;}cnt = 0;}memset(buc, 0, sizeof (buc));cnt = 0;ll all = 1, res = 1;h[n + 1] = 1;for (int i = n; i; i--) {all = all * ipw2[buc[a[i]]] % P;if (buc[a[i]])res = res * ipw1[buc[a[i]]] % P;elsecnt++;buc[a[i]]++;all = all * pw2[buc[a[i]]] % P;res = res * (pw2[buc[a[i]]] + P - 1) % P;h[i] = (all + P - (cnt == c ? res : 0)) % P;}f[0][0] = 1;for (int i = 1; i * c <= n; i++)for (int j = c * i; j <= n; j++) {for (int k = (i - 1) * c; k <= n && g[k + 1][j]; k++) {f[i][j] += f[i - 1][k] * g[k + 1][j];if (!(k & 15))f[i][j] %= P;}f[i][j] %= P;}for (int i = 0; i <= n; i++) {ll ans = 0;for (int j = c * i; j <= n; j++)(ans += f[i][j] * h[j + 1]) %= P;if (i * c > n)ans = i == 0;printf("%lld%c", ans - (i == 0), " \n"[i == n]);}
}
}
namespace SolveS {
int f[2][3005][1 << 10];
void Work() {for (int i = 1; i <= n; i++)a[i]--;f[0][0][0] = 1;for (int i = 0; i < n; i++) {int o = i & 1;for (int j = 0; j * c <= i; j++)for (int S = 0; S < (1 << c); S++) {(f[o ^ 1][j][S] += f[o][j][S]) %= P;if ((S | (1 << a[i + 1])) == (1 << c) - 1)(f[o ^ 1][j + 1][0] += f[o][j][S]) %= P;else(f[o ^ 1][j][S | (1 << a[i + 1])] += f[o][j][S]) %= P;}for (int j = 0; j * c <= i; j++)for (int S = 0; S < (1 << c); S++)f[o][j][S] = 0;}for (int i = 0; i <= n; i++) {int ans = 0;for (int S = 0; S < (1 << c); S++)(ans += f[n & 1][i][S]) %= P;printf("%d%c", (ans + P - (i == 0)) % P, " \n"[i == n]);}
}
}
int main() {scanf("%d%d", &n, &c);for (int i = 1; i <= n; i++)scanf("%d", a + i);if (c > 10)return SolveB::Work(), 0;SolveS::Work();return 0;
}