CF1801E Gasoline prices 题解

\(\text{CF1801E Gasoline prices 题解}\)

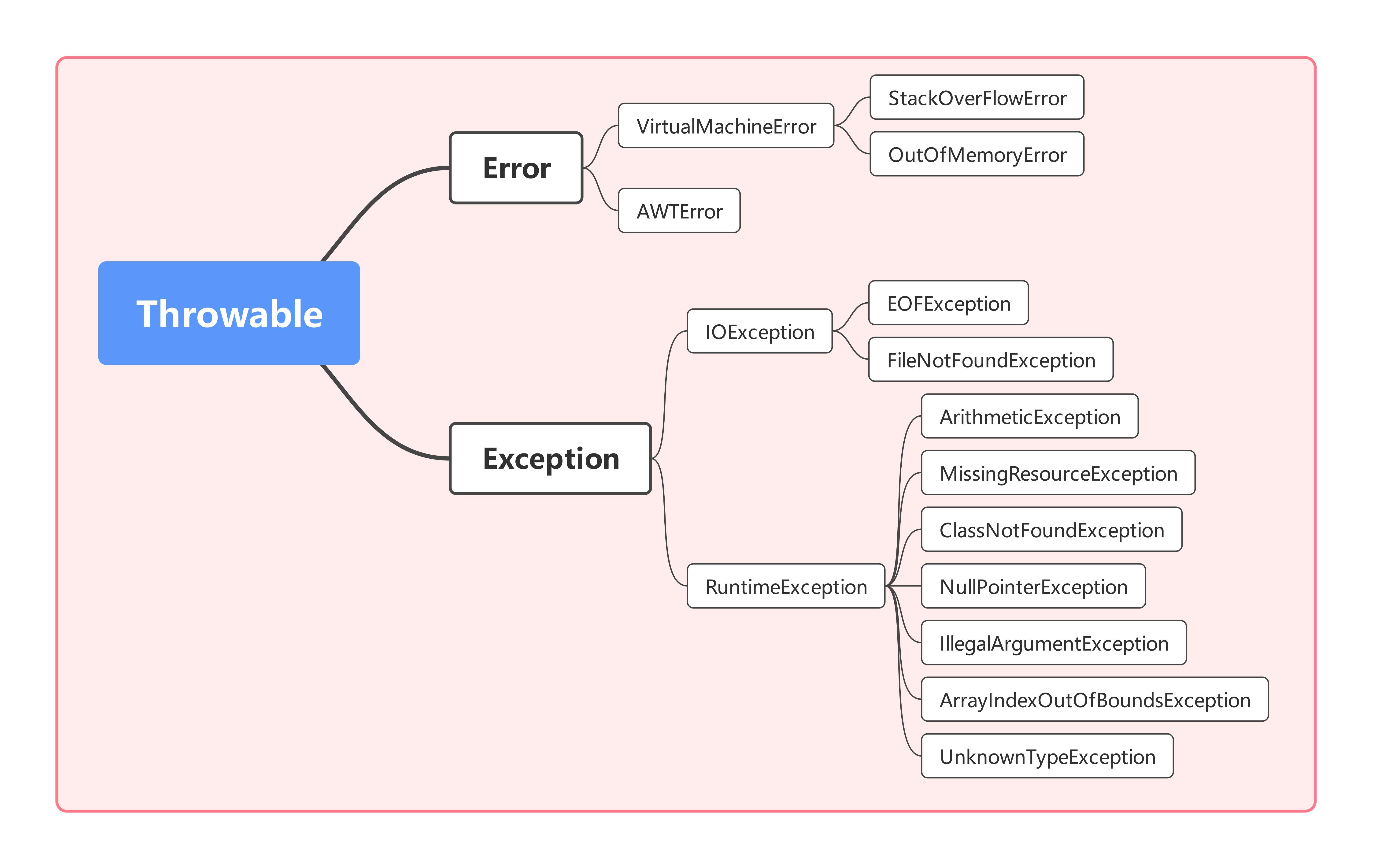
考虑方案数如何计算。注意到树上一些点有着相同的取值，于是如果我们将它们用并查集缩起来，它的可行取值范围就是 \([\max_{l_i},\min_{r_i}]\)。现在考虑并查集的维护方式。考虑只有 \(n\) 个点，这样一来需要合并的点对至多只有 \(O(n)\) 个，也就是我们只需要快速地找到两条路径上所属不同集合的点即可。现在考虑如何处理这玩意。由于总的合并个数只有 \(n\)，因此在并查集合并的时候可以顺便启发式合并出每个点现在属于哪个根节点下。这个过程中我们用树上数据结构维护一下信息，查询的时候二分去做一下就行了。看上去很好实现的样子。

然后我们考虑怎么实现。启发式合并直接用 std::set 就可以暴力做。对于一条路径我们可以拆成两条链，分类讨论维护一下信息即可。这个树上数据结构第一想法是线段树结合树链剖分，但这样一来内层的复杂度是 \(O(\log^2n)\) 的，总的复杂度是 \(O(n\log^3 n)\)，亲测过不去。考虑维护的实际上是一条链的信息，能够做贡献的只有父亲节点，于是考虑维护每个点对于子树内的贡献，查询的时候差分一下就行了，总的时间复杂度是 \(O(n\log^2n)\)，略微卡常。看上去很好实现的样子，只有区区 4.5 KiB。

#include <bits/stdc++.h>
#define N 200005
#define M 18
#define ull unsigned long long
#define ll long long
#define mod 1000000007
using namespace std;
ll qpow(ll x) {ll y = mod - 2, ans = 1;while (y) {if (y & 1) ans = ans * x % mod;x = x * x % mod;y >>= 1;}return ans;
}
int n;
struct node {int to, nxt;
} t[N];
int head[N], cnt;
void add(int u, int v) {t[++cnt].to = v;t[cnt].nxt = head[u];head[u] = cnt;
} 
int dfn[N], rk[N], tot;
int dep[N], siz[N], anc[M][N], top[N], son[N], f[N];
int tpt;
void dfs1(int x, int fa) {f[x] = anc[0][x] = fa;dep[x] = dep[fa] + 1;siz[x] = 1;for (int i = head[x]; i; i = t[i].nxt) {int y = t[i].to;dfs1(y, x);siz[x] += siz[y];if (siz[son[x]] < siz[y]) son[x] = y;}
}
void dfs2(int x, int tp) {dfn[x] = ++tot;rk[tot] = x;top[x] = tp;if (!son[x]) return;dfs2(son[x], tp);for (int i = head[x]; i; i = t[i].nxt) if (t[i].to != son[x])dfs2(t[i].to, t[i].to);
}
int LCA(int x, int y) {while (top[x] != top[y]) {if (dep[top[x]] < dep[top[y]]) swap(x, y);x = f[top[x]];}return dep[x] > dep[y] ? y : x;
}
const ull bas = 131;
ull fac[N], inv[N];
int tqt;
struct BIT {int lbt(int x) {return x & (-x);}ull tree[N];void ad(int x, ull vl) {++tqt;while (x <= n) tree[x] += vl, x += lbt(x);}void add(int x, int y, ull vl) {ad(x, vl);ad(y + 1, -vl);}ull ask(int x) {++tqt;ull ans = 0;while (x) ans += tree[x], x -= lbt(x);return ans;}
} U, D;
ll ans = 1;
int ml[N], mr[N];
struct DSU {int fa[N];int fnd(int x) {return x == fa[x] ? x : fa[x] = fnd(fa[x]);}set<int>st[N];int l[N], r[N];void mge(int x, int y) {x = fnd(x), y = fnd(y);if (x == y) return;if (st[x].size() < st[y].size()) swap(x, y);fa[y] = x;ans = ans * qpow(r[x] - l[x] + 1) % mod;ans = ans * qpow(r[y] - l[y] + 1) % mod;l[x] = max(l[x], l[y]), r[x] = min(r[x], r[y]);ans = ans * max(r[x] - l[x] + 1, 0) % mod;for (auto i : st[y]) {st[x].insert(i);U.add(dfn[i], dfn[i] + siz[i] - 1, (x - y) * fac[dep[i]]);D.add(dfn[i], dfn[i] + siz[i] - 1, (x - y) * inv[dep[i]]);}st[y].clear();}void init() {for (int i = 1; i <= n; i++) {fa[i] = i;l[i] = ml[i], r[i] = mr[i];ans = ans * (mr[i] - ml[i] + 1) % mod;U.add(dfn[i], dfn[i] + siz[i] - 1, i * fac[dep[i]]);D.add(dfn[i], dfn[i] + siz[i] - 1, i * inv[dep[i]]);st[i].insert(i);}}
} dsu;
ull gt(int x, int y) { return (U.ask(dfn[x]) - U.ask(dfn[f[y]])) * inv[dep[y]];
}
ull tg(int x, int y) {return (D.ask(dfn[y]) - D.ask(dfn[f[x]])) * fac[dep[y]];
}
vector<int>v[N];
int gtk(int x, int k) {++tpt;for (int i = M - 1; i >= 0; i--)if ((k >> i) & 1) x = anc[i][x];return x;
}
ull fnd(int x, int y, int k, int l) {if (dep[l] + k <= dep[x]) {int p = gtk(x, k);return gt(x, p);} ull ans = gt(x, l);k -= dep[x] - dep[l];int p = gtk(y, dep[y] - dep[l] - k);return ans * fac[k] + tg(gtk(y, dep[y] - dep[l] - 1), p);
}
int fd(int x, int y, int k, int l) {if (dep[l] + k <= dep[x]) return gtk(x, k);k -= dep[x] - dep[l];int p = gtk(y, dep[y] - dep[l] - k);return p;
}
ull qw(ull x, ull y) {ull ans = 1;while (y) {if (y & 1) ans *= x;x *= x;y >>= 1;}return ans;
}
int main() {fac[0] = inv[0] = 1;for (int i = 1; i < N; i++) fac[i] = fac[i - 1] * bas;ull ivb = qw(fac[1], ULONG_LONG_MAX);for (int i = 1; i < N; i++) inv[i] = inv[i - 1] * ivb;ios::sync_with_stdio(0);cin.tie(0);cin >> n;for (int i = 2; i <= n; i++) {int x;cin >> x;add(x, i);}for (int i = 1; i <= n; i++) cin >> ml[i] >> mr[i];for (int i = 0; i <= n; i++) {for (int j = M - 1; j >= 0; j--)if ((i >> j) & 1)v[i].push_back(j);}dfs1(1, 0);dfs2(1, 1);for (int j = 1; j < M; j++)for (int i = 1; i <= n; i++)anc[j][i] = anc[j - 1][anc[j - 1][i]];dsu.init();int q;cin >> q;while (q--) {int a, b, c, d;cin >> a >> b >> c >> d;if (ans == 0) {cout << "0\n";continue;}int la = LCA(a, b), lc = LCA(c, d), lh = dep[a] + dep[b] - 2 * dep[la];while (fnd(a, b, lh, la) != fnd(c, d, lh, lc)) {int l = 0, r = lh, mid = 0, as = 0;while (l <= r) {mid = (l + r) >> 1;if (fnd(a, b, mid, la) != fnd(c, d, mid, lc)) as = mid, r = mid - 1;else l = mid + 1;} int na = fd(a, b, as, la), nc = fd(c, d, as, lc);dsu.mge(na, nc);}cout << ans << "\n";}return 0;
}