AI应用实战课学习总结（5）回归分析预测实战

news/2025/1/13 8:32:31/文章来源:https://www.cnblogs.com/edisonchou/p/18667411/ai-in-practice-notes-session5

大家好，我是Edison。

最近入坑黄佳老师的《AI应用实战课》，记录下我的学习之旅，也算是总结回顾。

今天是我们的第5站，一起了解下回归分析是什么以及通过回归模型预测电商用户的生命周期价值（LTV）。

回归分析介绍

通过分析已有的数据，发现之间的关系，这就是回归分析。

所谓回归，就是让数据恢复其本来规律，用黑话讲就是建立特征与目标之间的映射关系，事实上呢就是求某种平均值。而我们想要找的这个关系，其实就是一个数学模型，它在统计学中通常被称为预测函数。

举个例子，给定一些父亲和儿子身高的数据，将其画在二维坐标系中，就是一个个点，有没有可能从中分析找到一个准确的数学模型描述这种关系，进而可以预测一个人的升高呢，这就是统计学中经典的回归问题，这个要找到的数学模型就是预测函数。得到了这个预测函数，以后当给定一个新的父亲身高的参数时就可以预测一个较为准确的子女身高数值了。

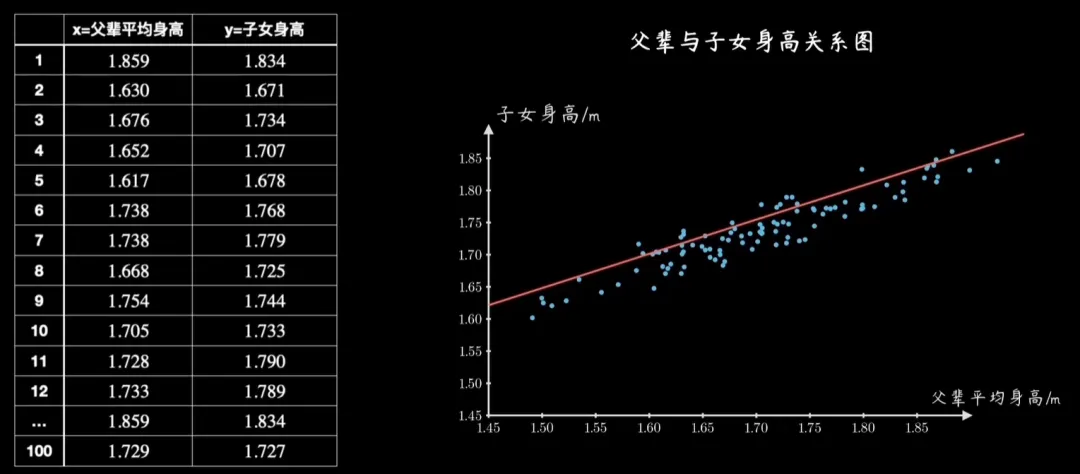
回归分析主要有两种类别：

根据变量的数目，可以分为一元回归和多元回归；
根据自变量和因变量的表现形式，可以分为线性回归和非线性回归。

回归分析主要应用在以下场景：

确定变量之间的关系
预测数值
趋势分析

我们在第三站《预测带货直播销售额》就是一个典型的回归分析案例。当然，回归算法有很多种，那篇文章中使用到的线性回归只是其中最简单的一种。

这里，Edison强烈推荐大家学习B站博主“五分钟机器学习”的视频，它在基础篇通俗易懂地讲解了线性回归、逻辑回归、K近邻、决策树、KMeans、SVM、随机森林等算法，在进阶篇中介绍了梯度下降算法，简洁易懂，适合快速扫盲。

传送门：https://space.bilibili.com/10781175/channel/series

此外，B站博主“梗直哥”有一个关于线性回归、代价函数、损失函数的动画讲解，个人觉得是我目前看到这个话题讲的最通俗易懂的，也推荐给你看看，你可以了解到一些核心内容，如线性回归模型、最小二乘法、均方误差以及梯度下降法。

传送门：https://www.bilibili.com/video/BV1RL411T7mT

因为这些博主的讲解已经是很通俗易懂并且真的讲的不错了，这里Edison就不再多赘述了。相信有了上面这些基础，我们就可以开始下面的回归模型实战了。

预测电商用户LTV案例

问题背景：

某电商系统记录了过去12个月的订单数据
订单数据包括：用户ID、购买物品、金额、时间等

问题目标：

根据历史数据，确定类似用户的生命周期价值（LTV，Life Time Value）

生命周期价值（LTV），它是衡量一个用户在其整个生命周期内为企业带来的总价值的一个指标。它考虑了用户的获取成本、留存率、复购率以及用户的平均消费额等多个因素，对于企业的长期规划和盈利分析至关重要。

回归分析代码实战

Step1 读取数据及数据预处理

import numpy as np # 导入NumPy
import pandas as pd # 导入Pandas
df_sales = pd.read_csv('eshop-orders.csv') # 导入数据集
df_sales # 输出数据

输出的数据展现成下面的样子：

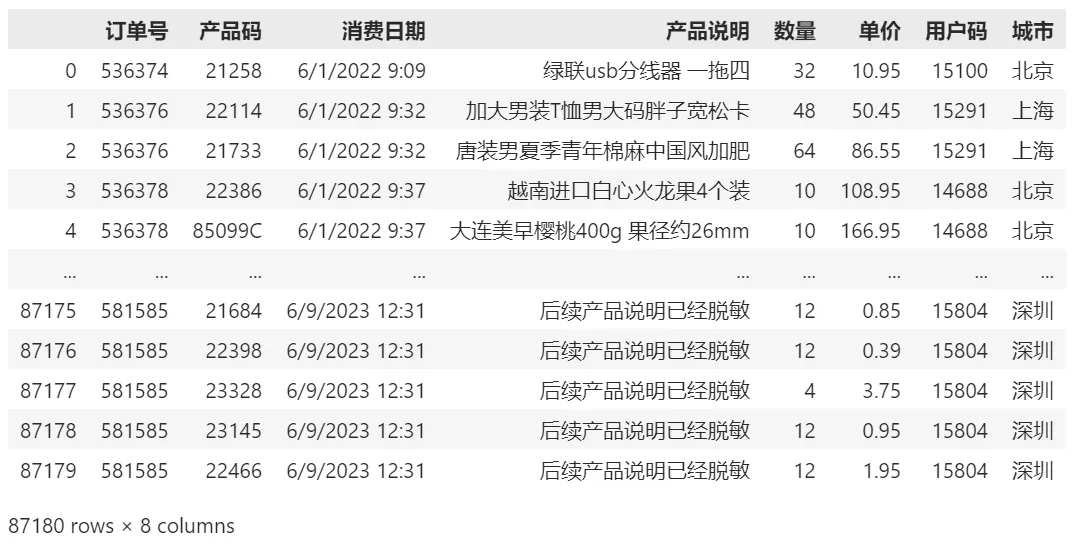
由于订单数据中只有每单的单价，因此我们先计算下每单的总价：

df_sales['总价'] = df_sales['数量'] * df_sales['单价'] # 计算每单的总价

然后我们看看订单数据的日期范围在哪个区间内：

df_sales['消费日期'] = pd.to_datetime(df_sales['消费日期']) # 转换日期格式
print('日期范围: %s ~ %s' % (df_sales['消费日期'].min(), df_sales['消费日期'].max()))# 输出日期范围

输出的日期范围：2022-06-01 09:09:00 ~ 2023-06-09 12:31:00然后我们先构建一个前3个月的数据集，先用这个数据集去做特征工程和测试，看看能否去预测用户未来一年的LTV。

df_sales_3m = df_sales[(df_sales. 消费日期 > '2022-06-01') & (df_sales. 消费日期 <= '2022-08-30')] # 构建仅含前3个月数据的数据集
df_sales_3m.reset_index(drop=True) # 重置索引

可以看到，数据从8.7万行到1.4万行了：

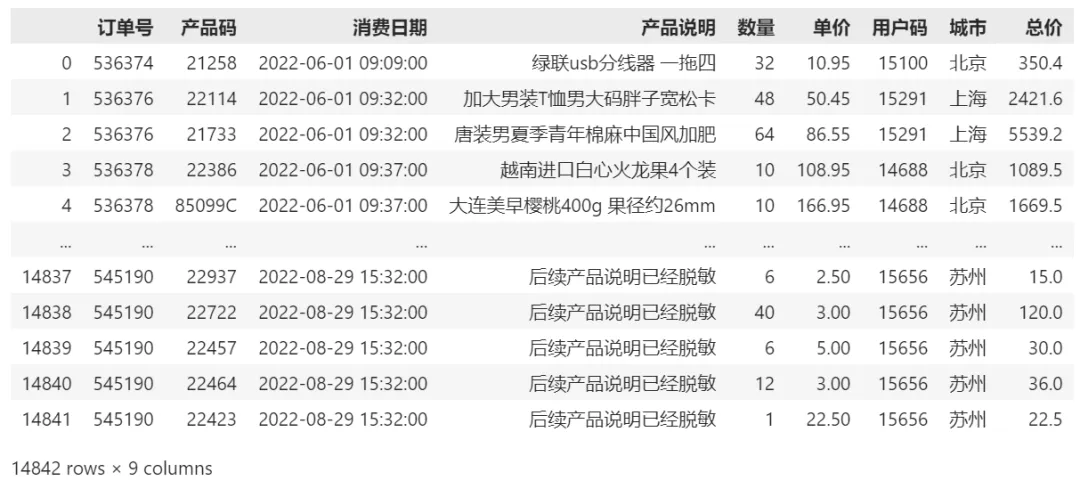
最后，我们获取一下用户ID列表（数据去重）：

数据去重后，共计370个用户：

Step2 特征工程

这里我们将原始订单数据转换为每一个用户的R、M、F值，R指Recency（用户的新近度，用来衡量用户是否在近期进行了消费），M指Money（用户共计消费了多少钱），F指Frequency（用户共计进行了多少次交易，即消费的频次）。
从这里我们也可以看出，在做这类用户交易数据分析时，不仅仅要看用户的共计消费金额，还需要将这些用户特征都考虑进去，才能对用户进行一个较为准确的画像。举个例子，有的用户可能在该电商平台中消费了很多钱，其他可能就是一次性买了一个高端电脑，然后就跟电商平台说拜拜了。那么，这个用户的M值就很大，比如10000元。但是，他的F值很低，只有1次。

因此，这个用户最后的LTV会是一个综合考量后的值。下面的代码展示了本示例中的R、M、F值的抽取：

# Recency
df_R_value = df_sales_3m.groupby('用户码'). 消费日期.max().reset_index() # 找到每个用户的最近消费日期，构建df_R_value 对象
df_R_value.columns = ['用户码','最近购买日期'] # 设定字段名
df_R_value['R值'] = (df_R_value['最近购买日期'].max() - df_R_value['最近购买日期']).dt.days # 计算最新日期与上次消费日期间的天数
df_user_LTV = pd.merge(df_user_LTV, df_R_value[['用户码','R值']], on='用户码') # 把上次消费日期距最新日期的天数（R 值）整合至df_user 对象中# Money
df_M_value = df_sales_3m.groupby('用户码').总价.sum().reset_index() # 计算每个用户前3 个月的消费总额，构建df_M_value 对象
df_M_value.columns = ['用户码','M值'] # 设定字段名
df_user_LTV = pd.merge(df_user_LTV, df_M_value, on='用户码') # 把消费总额（M 值）整合至df_user对象中# Frequency
df_F_value = df_sales_3m.groupby('用户码'). 消费日期.count().reset_index() # 计算每个用户的消费次数，构建df_F_value 对象
df_F_value.columns = ['用户码','F值'] # 设定字段名
df_user_LTV = pd.merge(df_user_LTV, df_F_value[['用户码','F值']], on='用户码') # 把消费频率(F 值)整合至df_user 对象中

df_user_LTV.head() # 输出df_user_LTV 的前几行数据

展示的前几行R、M、F值数据：

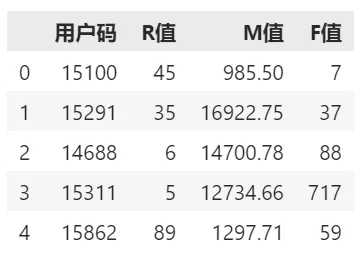
现在我们有了特征（X），就需要再得到标签（y）了。这里的标签就是我们要预测的年度LTV值，特征就是R、M、F三个值。

df_user_1y = df_sales.groupby('用户码')['总价'].sum().reset_index() # 计算每个用户的整年消费总额，构建df_user_1y 对象
df_user_1y.columns = ['用户码','年度LTV'] # 设定字段名

df_LTV = pd.merge(df_user_LTV, df_user_1y, on='用户码', how='left') # 计算整体LTV，训练数据集
df_LTV # 输出df_LTV

到此，一个完整的特征集和标签的每个用户的LTV表如下，从中我们也可以看出每个用户的年度LTV 和他的R/M/F值的一些关系：

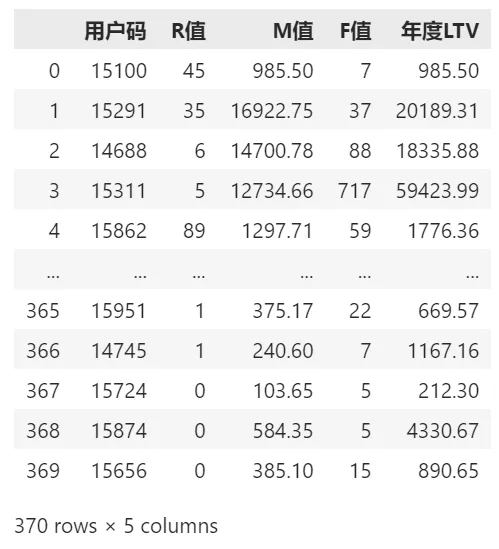
X = df_LTV.drop(['用户码','年度LTV'],axis=1) # 特征集
X.head() # 输出特征集 ：R,M,F值

y = df_LTV['年度LTV'] # 标签集
y.head() #输出标签集 ：LTV值

Step3 拆分训练集和测试集

这里我们选择80%训练集，20%测试集：

from sklearn.model_selection import train_test_split #导入train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7) #拆分训练集和测试集

Step4 使用线性回归拟合模型

from sklearn.linear_model import LinearRegression #导入线性回归模块
model = LinearRegression() #创建线性回归模型

model.fit(X_train, y_train) #拟合模型

Step5 评估线性回归拟合效果

y_train_preds =  model.predict(X_train) # 用模型预测训练集
y_test_preds = model.predict(X_test) # 用模型预测测试集from sklearn.metrics import r2_score, median_absolute_error #导入Sklearn评估模块
print('训练集上的R平方分数: %0.4f' % r2_score(y_true=y_train, y_pred=y_train_preds))
print('测试集上的R平方分数: %0.4f' % r2_score(y_true=y_test, y_pred=y_test_preds))

得到的R平方分数如下：

训练集上的R平方分数: 0.6187

测试集上的R平方分数: 0.4778

可以看出，它在训练集上的效果还不错，但在测试集上的分数差了一丢丢，但也没差多少吧。

Step6 拟合效果数据可视化

这里仍然使用matplotlib绘制一个散点图和预测直线做数据可视化，看看模型的预测值和实际值的差异对比：

import matplotlib.pyplot as plt # 导入Matplotlib 的pyplot 模块
plt.rcParams["font.family"]=['SimHei'] #用来设定字体样式
plt.rcParams['font.sans-serif']=['SimHei'] #用来设定无衬线字体样式
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.scatter(y_test, y_test_preds) # 预测值和实际值的散点图
plt.plot([0, max(y_test)], [0, max(y_test_preds)], color='gray', lw=1, linestyle='--') # 绘图
plt.xlabel(' 实际值') #x 轴
plt.ylabel(' 预测值') #y 轴
plt.title(' 实际值与预测值') # 标题

最终的预测直线如下所示：

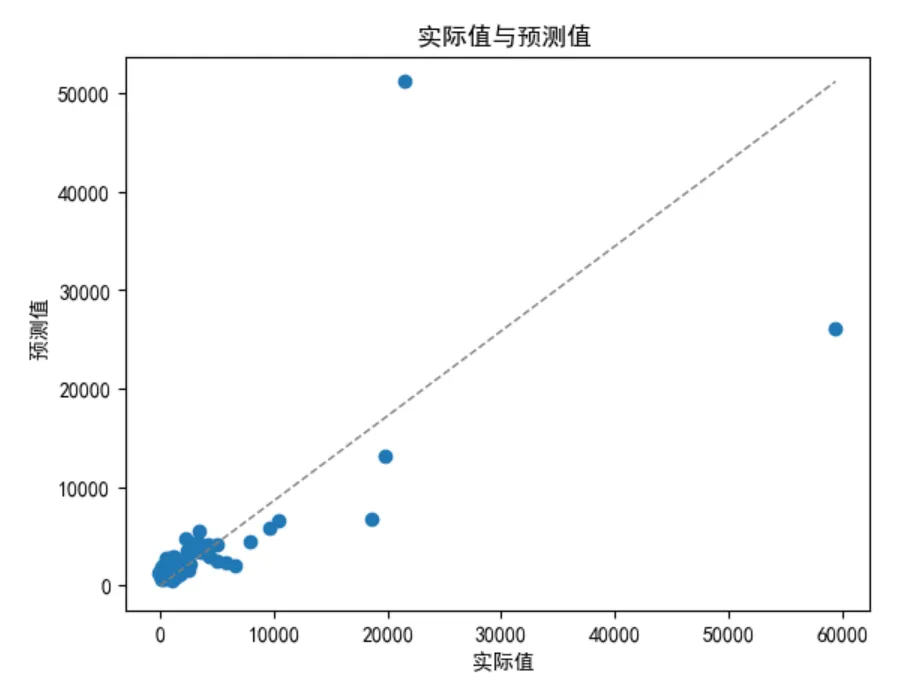
Step7 更多回归模型做对比

除了线性回归之外，我们可以用多种回归模型来做一个效果的对比，比如下面我们引入决策树和随机森林来和线性回归一起做个对比，修改一下之前的代码如下：

（1）导入模型和创建模型

from sklearn.linear_model import LinearRegression #导入线性回归模块
from sklearn.tree import DecisionTreeRegressor #导入决策树回归模型
from sklearn.ensemble import RandomForestRegressor #导入随机森林回归模型

model_lr = LinearRegression() #创建线性回归模型
model_dtr = DecisionTreeRegressor() #创建决策树回归模型
model_rfr = RandomForestRegressor() #创建随机森林回归模型

（2）进行拟合

model_lr.fit(X_train, y_train) #拟合线性回归模型
model_dtr.fit(X_train, y_train) #拟合决策树回归模型
model_rfr.fit(X_train, y_train) #拟合随机森林回归模型

（3）得到R平方分数

from sklearn.metrics import r2_score, median_absolute_error #导入Sklearn评估模块# 线性回归
y_train_preds =  model_lr.predict(X_train) # 用模型预测训练集
y_test_preds = model_lr.predict(X_test) # 用模型预测测试集
print('线性回归 - 训练集上的R平方分数: %0.4f' % r2_score(y_true=y_train, y_pred=y_train_preds))
print('线性回归 - 测试集上的R平方分数: %0.4f' % r2_score(y_true=y_test, y_pred=y_test_preds))# 决策树回归
y_train_preds =  model_dtr.predict(X_train) # 用模型预测训练集
y_test_preds = model_dtr.predict(X_test) # 用模型预测测试集
print('决策树回归 - 训练集上的R平方分数: %0.4f' % r2_score(y_true=y_train, y_pred=y_train_preds))
print('决策树回归 - 测试集上的R平方分数: %0.4f' % r2_score(y_true=y_test, y_pred=y_test_preds))# 随机森林回归
y_train_preds =  model_rfr.predict(X_train) # 用模型预测训练集
y_test_preds = model_rfr.predict(X_test) # 用模型预测测试集
print('随机森林回归 - 训练集上的R平方分数: %0.4f' % r2_score(y_true=y_train, y_pred=y_train_preds))
print('随机森林回归 - 测试集上的R平方分数: %0.4f' % r2_score(y_true=y_test, y_pred=y_test_preds))