side channel

‌Side Channel‌，中文称为“边信道”，是指通过加密软件或硬件运行时产生的各种泄漏信息来获取密文信息的攻击方式。在狭义上，边信道攻击特指针对密码算法的非侵入式攻击，通过分析加密电子设备在运行过程中的边信道信息泄露来破解密码算法。常见的边信道攻击包括计时攻击、能量分析攻击、电磁分析攻击等‌12。

边信道攻击的类型

1. ‌计时攻击‌：通过分析加密设备运行时的时序信息来获取密文信息。
2. ‌能量分析攻击‌：包括简单功耗分析（SPA）和差分功耗分析（DPA），通过分析加密设备运行时的功耗信息来获取密文信息。
3. ‌电磁分析攻击‌：通过分析设备运行时产生的电磁辐射来获取密文信息。
4. ‌错误攻击‌：通过制造运行错误来获取密文信息‌2。

边信道攻击的背景和历史

边信道攻击的研究始于1996-1999年，传统的分组密码分析技术局限于算法的数学结构，而边信道攻击通过利用加密设备在运行过程中的额外信息（如功耗、电磁泄漏等），其攻击效果显著，给密码设备带来了严重的威胁‌1。

实际应用中的例子

例如，在英特尔的SGX（Software Guard Extensions）技术中，边信道攻击被用来执行缓存计时攻击和AsyncShock攻击。缓存计时攻击通过固定两个内核线程到共享相同物理内核和L1缓存的逻辑内核，利用RDPMC指令完成对高速缓存行的探测。AsyncShock攻击则利用SGX Enclave中的同步漏洞，通过中断线程和删除页面的读取和执行权限来进行攻击‌3。

 

 

参考内容：Introduction to Modern Cryptography --3rd edition by Jonathan Katz et al., Chapter 7, Section 7.2.6 Differential and Linear Cryptanalysis

---

对于分组密码（SPN->Feistel Network->DES->3DES->AES），相对复杂的结构会使得分析更加复杂。但是我们要避免一个误区：并不是将分组密码设计得越复杂，其就越难被攻破。与期望的相反，构建一个安全的分组密码往往很难，但攻破一个分组密码（无论它有多难），往往是相对容易的多的。所以这提醒我们，非专业人士不要轻易尝试构造一个新的分组密码，而是利用现有的，被经过时间证明的分组密码来构建加密策略或是新的分组密码（3DES就是一个利用DES构造分组密码的很好例子）。

本文将介绍两种密码分析工具——差分密码分析和线性密码分析，来浅略地接触一下高级密码分析，同时再次提醒：“在设计新的、安全的分组密码时，需要谨慎选择构造其的组件”。

差分密码分析

这种技术是在上世纪80年度末由Biham和Shamir等人提出，并在1993年用于攻击DES。这种分析/攻击方式的思想在于：将特定的输入差异和对应的输出差异列成表格，寻找其中期望概率大于基于随机置换发生的概率的输入输出差异。

简单来说，如果有一个随机置换 𝑃P 和置换 𝐺𝑘G_k ，有两个不同的输入 𝑥1,𝑥2x_1,x_2 ，这两个输入的差异表示为 Δ𝑥=𝑥1⊕𝑥2\Delta_x=x_1\oplus{x_2} 。给定一个输出差异值 Δ𝑦:=𝑦𝑖⊕𝑦𝑗\Delta_y:=y_i\oplus{y_j} ，在随机置换下，输入 𝑥1,𝑥2x_1,x_2 对应的输出的差异恰好为 Δ𝑦\Delta_y 的概率为 𝑃𝑟[𝑃(𝑥1)⊕𝑃(𝑥2)=Δ𝑦]=2−𝑙\mathbf{Pr}[P(x_1)\oplus{P(x_2)}=\Delta_y]=2^{-l} ( 𝑙l 为分组密码的分组/输入输出长度)，但是在置换 𝐺𝑘G_k 下，输入 𝑥1,𝑥2x_1,x_2 对应的输出的差异恰好为 Δ𝑦\Delta_y 的概率 𝑝p 可能是远大于/远小于 2−𝑙2^{-l} 的（因为这个置换是伪随机的）。

敌手可以通过抓住输入输出差异显著高于随机置换下发生的情况，对其进行密钥恢复的攻击。以下讨论将基于SPNs（Substitution Permutation Networks），从理论上分析如何攻破一个SPNs中所有的sub-keys。

分析基本思路（以SPN为例）

假设 𝐹F 表示 𝑙l 位长的 𝑟r 轮SPN， 𝐺𝑘(∗)G_k(*) 表示 𝐹F 的前 𝑟−1r-1 轮和第 𝑟r 轮的Key mixing阶段，并且我们已经找到一组输入输出差异 (Δ𝑥,Δ𝑦)(\Delta_x,\Delta_y) 使得这组差异在 𝐺𝑘(∗)G_k(*) 中发生的概率为 𝑝≫2−𝑙p\gg{2^{-l}} 。当敌手知道足够多的满足输入差异的输入对时，即 {(𝑥1𝑖,𝑥2𝑖)}𝑖=1𝐿\{(x_1^i,x_2^i)\}^L_{i=1} ，满足 ∀𝑖∈{1,…,𝐿},𝑥1𝑖⊕𝑥2𝑖=Δ𝑥\forall{i}\in\{1,\dots,L\},x_1^i\oplus{x_2^i}=\Delta_x ，就可以恢复出最后一次Key mixing对应的sub-key 𝑘𝑟+1k_{r+1} ：

1. 通过 𝐹F 计算所有输入对对应的输出对 {(𝑦1𝑖,𝑦2𝑖)}𝑖=1𝐿,𝑦=𝐹(𝑥)\{(y_1^i,y_2^i)\}^L_{i=1},y=F(x)
2. 穷举最后一次key mixing对应的sub-key 𝑘𝑟+1∈{0,1}𝑙k_{r+1}\in\{0,1\}^l ，对所有的 {(𝑦1𝑖,𝑦2𝑖)}𝑖=1𝐿\{(y_1^i,y_2^i)\}^L_{i=1} 进行逆操作（inverse key mixing->inverse mixing permutation->inverse substitution），得到对应的 {{(𝑦1𝑖−,𝑦2𝑖−)}𝑖=1𝐿}|𝐾|,𝑘𝑟+1∈𝐾\{\{(\overset{-}{y_1^i},\overset{-}{y_2^i})\}^L_{i=1}\}^{|\cal{K}|},k_{r+1}\in\cal{K} ，这些值等价于 𝑦−=𝐺𝑘(𝑥)\overset{-}{y}=G_k(x) 。
3. 对每一个 {(𝑦1𝑖−,𝑦2𝑖−)}𝑖=1𝐿\{(\overset{-}{y_1^i},\overset{-}{y_2^i})\}^L_{i=1} ，计算 𝑦1𝑖−⊕𝑦2𝑖−=Δ𝑦\overset{-}{y_1^i}\oplus\overset{-}{y_2^i}=\Delta_y 的概率，若其概率近似 𝑝p ，则其对应的 𝑘𝑟+1k_{r+1} 为最后一轮key mixing的sub-key，接下来，降低轮数，迭代求出前 𝑟r 次key mixing的sub-key，从而完成攻击。

这样的攻击所耗的时间复杂度约为 𝑂(𝐿⋅2𝑙)O(L\cdot2^l) ，但是针对SPN有一种可以时间耗时更少的攻击方式：将 𝑥,𝑦,𝑘x,y,k 按照S-box的长度进行分组，对每个分组单独进行穷举。由于各分组间相互独立，所以时间复杂度可降至 𝑂(𝐿⋅2𝑙/𝑛)O(L\cdot{2^{l/n}}) (此处 𝑛n 为S-box的长度)。但是要求对应的 𝑝≫2−𝑙/𝑛p\gg2^{-l/n} ，这样差分效果才能够显著。

对于 𝑝p 的讨论：前文多次提及 𝑝p 的大小，这是由于对于一个随机的sub-key，其生成的 {(𝑦1𝑖−,𝑦2𝑖−)}𝑖=1𝐿\{(\overset{-}{y_1^i},\overset{-}{y_2^i})\}^L_{i=1} 中满足 𝑦1𝑖−⊕𝑦2𝑖−=Δ𝑦\overset{-}{y_1^i}\oplus\overset{-}{y_2^i}=\Delta_y 的概率为 2−𝑙2^{-l} ，只有远大于才能与随机显著地区别开来。

寻找差分对

现在有一个4轮的SPN，其分组长度为16位，S-box的输入输出长度为4位。

其中，S-box的定义如下：

S-box输入输出表

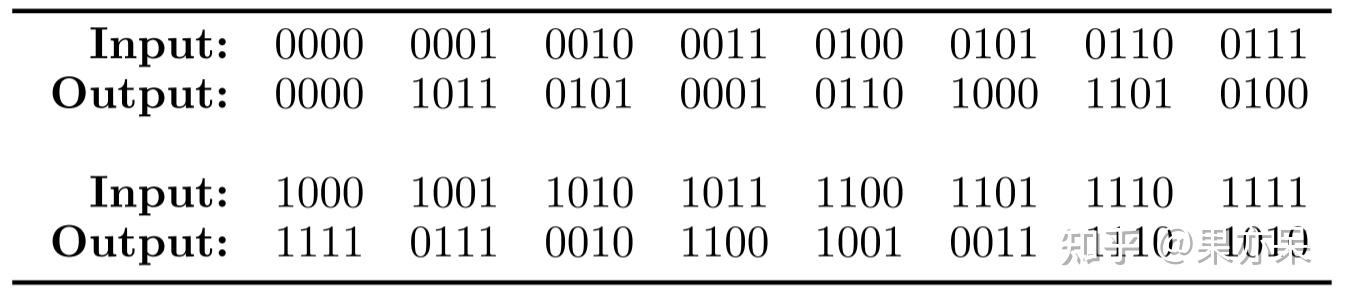
mixing permutation定义如下：

mixing permutation的交换索引表

1. 寻找S-box中的差分，遍历 𝑥∈{0,1}4,Δ𝑥∈{0,1}4x\in\{0,1\}^4,\Delta_x\in\{0,1\}^4 ，计算 𝑆(𝑥)⊕𝑆(𝑥+Δ𝑥)=Δ𝑦S(x)\oplus{}S(x+\Delta_x)=\Delta_y ，寻找 Δ𝑦\Delta_y 在某个 Δ𝑥\Delta_x 下会产生较大概率偏移（ 𝑝≫2−𝑙p\gg2^{-l} ），如下标，当 Δ𝑥=1111\Delta_x=1111 时， Δ𝑦=1010\Delta_y=1010 的概率为1/2。

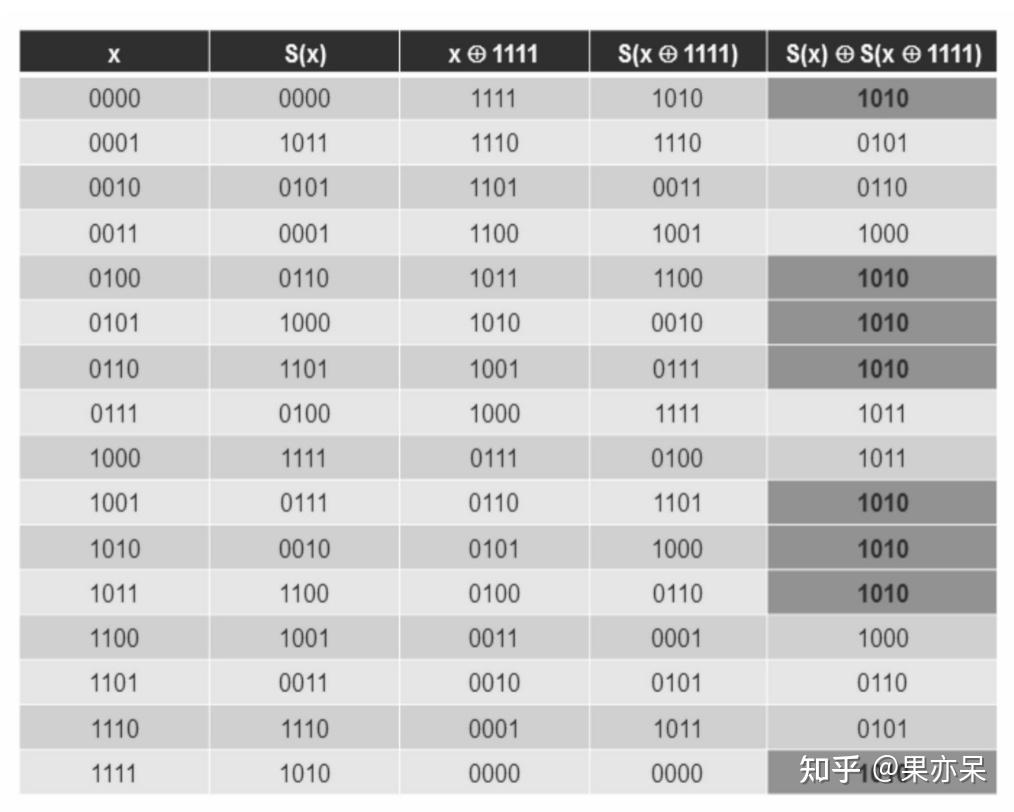
2. 我们对所有可能的值都进行穷举，形成如下表

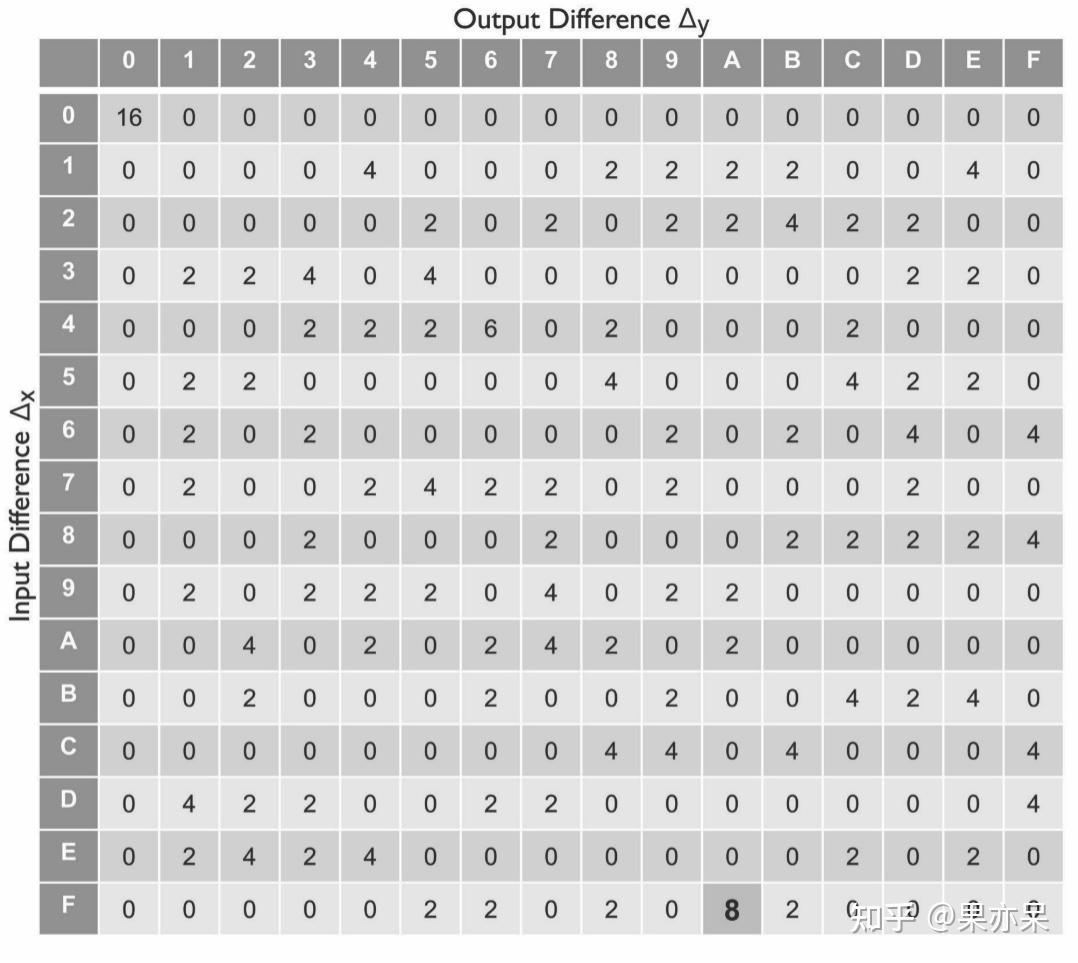
3. 我们对前三轮的SPN寻找差分，设差分值 Δ𝑥=0000 1100 0000 0000\Delta_x=0000\space1100\space0000\space0000 ：由于key mixing不会改变差分值，所以在第一轮的substitution阶段前差分值不变，经过第一轮S-box后，差分值 11001100 有 1/41/4 的概率变为 10001000，根据mixing permutation，差分值将影响第二轮的12号位（5->12），第二轮 00010001 差分值有 1/41/4 的概率变为 01000100 ，根据mixing permutation，差分值将影响第三轮的1号位（10->1），第三轮 10001000 差分值有 1/41/4 的概率变为 11111111 ，根据mixing permutation，差分值将影响第四轮的2、3、7、8号位。

4. 我们就找到了一组可用的 (Δ𝑥=0000 1100 0000 0000,Δ𝑦=0110 0011 0000 0000)(\Delta_x=0000\space1100\space0000\space0000,\Delta_y=0110\space0011\space0000\space0000) ，其发生的概率为 14⋅14⋅14=164≫2−16\frac{1}{4}\cdot\frac{1}{4}\cdot\frac{1}{4}=\frac{1}{64}\gg2^{-16} 。

为了提高效率，可以寻找低权值差分，即对第一轮前8位进行差分分析（输出位对应2\3\5\7\8\9\11\12位），应用上述所说的攻击方法，就能找到对应前8位的密钥；以相同的方式完成后半密钥的破解。

差分攻击的实际应用

对FEAL-8的攻击，在1991年，仅使用1000个选择明文，在两分钟内恢复密钥。FEAL-8在1987年计划替代DES，但是被轻易攻破了。现在的所有分组密码都需要经过差分攻击的测试。

差分攻击也成为了第一个对于DES攻击中优于简单穷举攻击的攻击方式，但是这种攻击方式依旧不高效，需要 2472^{47} 个选择明文。一个小趣闻，DES的设计者为了挫败差分攻击，特别对DES中的S-box专门进行了修改，这使得一旦对DES的S-box进行修改，就会使得DES十分容易收到差分攻击。

线性密码分析

线性密码分析抓住了输入、输出和密钥直接的线性关系，使得这种关系发生的概率足够高。

简单来说，从输入、输出和密钥各选择一位进行异或，寻找其结果为0的概率与1/2的偏置值，如果足够高，那么也可以通过类似方式来恢复密钥。

对分组密码设计的影响

现代分组密码的设计和评价在一定程度上基于其对差分和线性密码分析的抵抗力。在构造分组密码时，设计者选择s盒和其他组件，以最小化差分概率和线性偏差。要消除s盒中所有的高概率差分是不可能的：任何s盒中的某些差分都会比其他的发生得更频繁。尽管如此，这些偏差仍然可以最小化。此外，增加轮数(并谨慎选择混合排列)既可以降低差分概率，也会使密码分析师更难找到任何可以利用的差异。