P3586 [POI2015] Logistyka
题目描述
维护一个长度为 \(n\) 的序列,一开始都是 \(0\),支持以下两种操作:
U k a将序列中第 \(k\) 个数修改为 \(a\)。Z c s在这个序列上,每次选出 \(c\) 个正数,并将它们都减去 \(1\),询问能否进行 \(s\) 次操作。
每次询问独立,即每次询问不会对序列进行修改。
【数据范围】
对于 \(100\%\) 的数据,\(1\leq n,m\leq 10^6\),\(1\leq k,c\leq n\),\(0\leq a\leq 10^9\),\(1\leq s\leq 10^9\)。
比较有趣的思维题,我们翻译一下题面:
2. Z c s 在这个序列上,每次选出 \(c\) 个正数,并将它们都减去 \(1\),询问能否进行 \(s\) 次操作。
显然,对于一个数 \(a_i\) 它大于 \(s\) 的部分是不会产生贡献的,因为 \(a_i\) 最多被减去 \(s\) 。
然后我们思考一下用什么样的策略来减:
图片来源:BearBrine
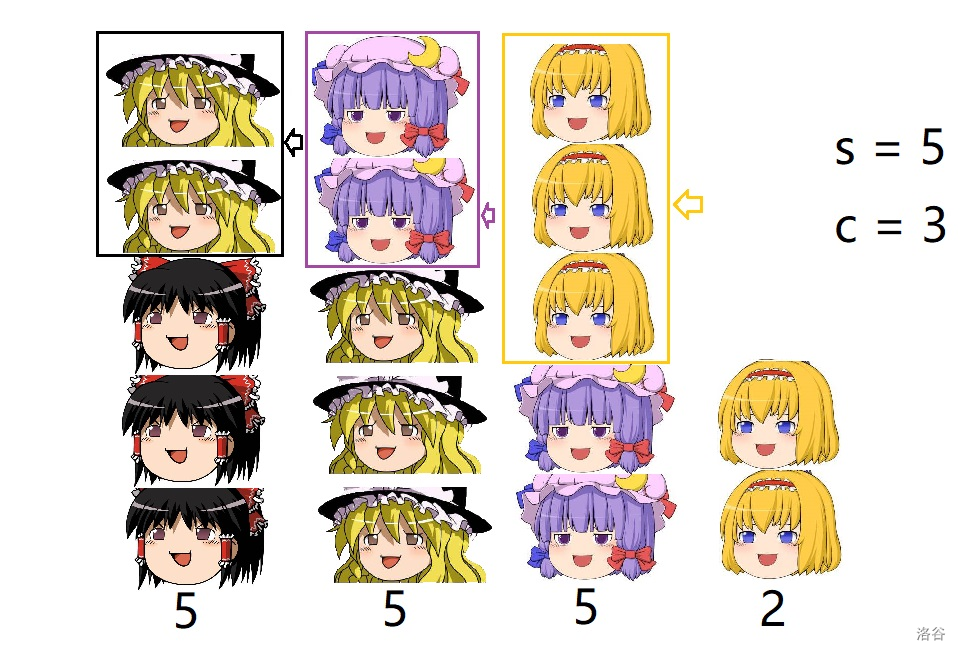
我们只需要将每堆东西不断的往左边移动,直到前一堆的高度等于 \(s\) 为止。那么我们最后的判断条件就是我们能否得到 \(c\) 堆高为 \(s\) 的东西。其实等价于:
\[\sum_{i=1}^{n} min(a_{i},s) \ge s*c
\]
所以我们用一个平衡树来维护这个东西,单点修改,查询时将平衡树按值域分裂为两部分。
对于 \([1,s]\) 它们对答案的贡献就是其总和,对于 \([s+1,inf]\) 其贡献为 \(cnt*s\)
然后这题就做完了
Code:
#include<bits/stdc++.h>
#define int long long
const int N=1e6+6;
using namespace std;
int n,m,cnt,rt;
int p[N];
//FHQ-Treap
struct Tree{int ls,rs,val,sum,siz,pri;
}t[N<<1];
int rd(){return rand()*rand()+rand()*17+1;}
int Node(int val){t[++cnt]={0,0,val,val,1,rd()};return cnt;}
void pushup(int x)
{t[x].siz=t[t[x].ls].siz+t[t[x].rs].siz+1;t[x].sum=t[t[x].ls].sum+t[t[x].rs].sum+t[x].val;}
void splite_val(int x,int &a,int &b,int k)
{if(!x){a=b=0;return ;}if(k>=t[x].val){a=x;splite_val(t[x].rs,t[x].rs,b,k);}if(k< t[x].val){b=x;splite_val(t[x].ls,a,t[x].ls,k);}pushup(x);//cout<<t[x].val<<" "<<k<<"="<<t[a].val<<" "<<t[b].val<<"\n";
}
void splite_siz(int x,int &a,int &b,int k)
{if(!x){a=b=0;return ;}int tmp=t[t[x].ls].siz+1;if(k>=tmp){a=x;splite_siz(t[x].rs,t[x].rs,b,k-tmp);}if(k< tmp){b=x;splite_siz(t[x].ls,a,t[x].ls,k);}pushup(x);
}
int merge(int x,int y)
{if(!x||!y)return x|y;if(t[x].pri< t[y].pri){t[x].rs=merge(t[x].rs,y);pushup(x);return x;}if(t[x].pri>=t[y].pri){t[y].ls=merge(x,t[y].ls);pushup(y);return y;}
}
char cc;
void work()
{ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++)p[i]=-1;int x,y,a,b,c;for(int i=1;i<=m;i++){cin>>cc;cin>>x>>y;if(cc=='U'){if(p[x]==-1){p[x]=y;splite_val(rt,a,b,p[x]);rt=merge(merge(a,Node(p[x])),b);}else{splite_val(rt,a,b,p[x]-1);splite_siz(b,b,c,1);rt=merge(a,c);p[x]=y;a=b=0;splite_val(rt,a,b,p[x]);rt=merge(merge(a,Node(p[x])),b);}}else{if(t[rt].siz<x||t[rt].sum<x*y){cout<<"NIE\n";continue;}splite_val(rt,a,b,y);int tmp=t[a].sum+t[b].siz*y;//cout<<t[a].sum<<" "<<t[b].siz<<" "<<y<<"="<<tmp<<"\n";cout<< (tmp>=x*y ? "TAK\n" : "NIE\n");rt=merge(a,b);}}
}
#undef int
int main()
{//freopen("Logistyka.in","r",stdin);freopen("Logistyka.out","w",stdout);work();return 0;
}