题目链接:
https://www.acwing.com/problem/content/319/
题目描述

提取题目大意:
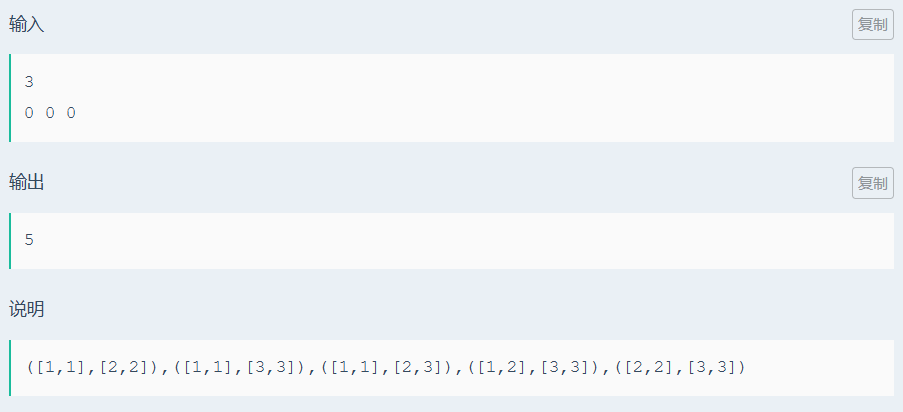
构造 L1对{},L2对[],L3对() 组成的深度为D的括号序列,求方案数。
并且中括号里不能有大括号,小括号里不能有中括号和大括号。
思路:考虑“第一段”括号序列(它作为一个整体,只能是{} [] 或 (),不能是其他)即划分成 {A}B、[A]B 或 (A)B,其中 A,B 是子问题。
我们没有必要枚举每一段的确切深度。
可以用a[i,j,k,l]表示深度不超过i,由j对{},k对[],l对()组成的括号序列数量。
最终答案变为 a[D,L1,L2,L3] - a[D-1,L1,L2,L3]
转移简化为:枚举第一段的最外层括号和枚举第一段的三种括号数
时间复杂度为 O(D*n^6)‘
但数据范围为
0≤L1,L2,L3≤10;
0≤D≤30。
是绰绰有余的
代码:
#include<iostream>
#include<algorithm>
using namespace std;
int a[31][11][11][11];
int L1, L2, L3, D;
int main() {cin >> L1 >> L2 >> L3 >> D;for (int i = 0; i <= D; i++) {a[i][0][0][0] = 1;}for (int i = 1; i <= D; i++) {for (int j = 0; j <= L1; j++) {for (int k = 0; k <= L2; k++) {for (int o = 0; o <= L3; o++) {if (j > 0) {for (int p = 1; p <= j; p++)for (int q = 0; q <= k; q++)for (int r = 0; r <= o; r++)a[i][j][k][o] = (a[i][j][k][o] + a[i - 1][p - 1][q][r] * a[i][j - p][k - q][o - r]) % 11380;}if (k > 0) {for (int q = 1; q <= k; q++)for (int r = 0; r <= o; r++)a[i][j][k][o] = (a[i][j][k][o] + a[i - 1][0][q - 1][r] * a[i][j][k - q][o - r]) % 11380;}if (o > 0) {for (int r = 1; r <= o; r++)a[i][j][k][o] = (a[i][j][k][o] + a[i - 1][0][0][r - 1] * a[i][j][k][o - r]) % 11380;}}}}}if (D) {cout << (a[D][L1][L2][L3] - a[D - 1][L1][L2][L3] + 11380) % 11380 << endl;}else {cout << (a[D][L1][L2][L3] +11380) % 11380 << endl;}
}