第一次
1. 神秘符文的重复序列


逻辑思维
#include<bits/stdc++.h>
using namespace std;
int main(){int n,k;cin>>n>>k;//长度为n,重复k遍!string s;cin>>s;long long int ans=0;long long int cnt=0;while(k--) {//重复k遍for(int i=0;i<n;i++){//遍历字符串sif(s[i]=='a'){cnt++;//已经经过几个a }else if(s[i]=='b'){ans+=cnt;//遇见一个b,就可以与前面的a搭配,所以要加上前面所有a }}}cout<<ans; return 0;
}2. 伦太郎的胡椒博士汽水
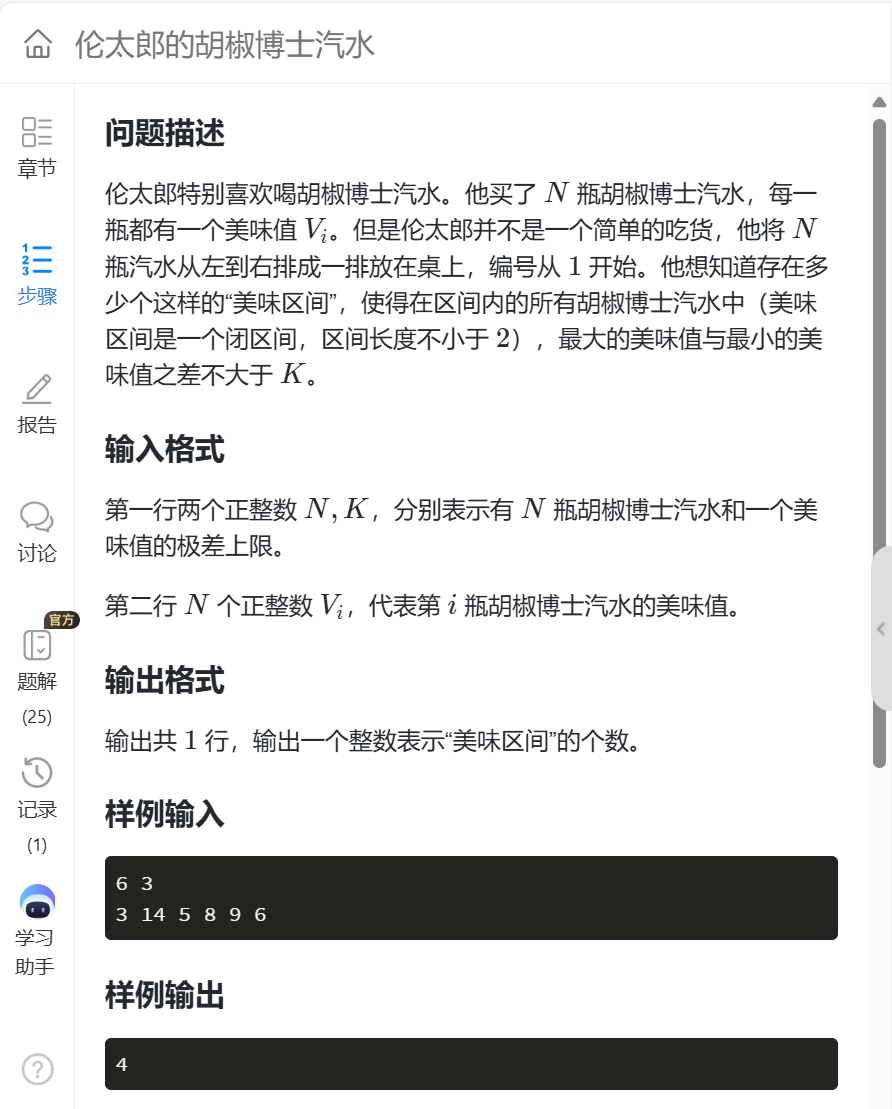

双指针算法:
一个指针标志起点,一个指针标志终点,序号从1到n
然后每次记录最大值,最小值,如果当前数字与当前的区间最大值差值大于k就break
双指针
#include<bits/stdc++.h>
using namespace std;
const long long int N=1e5+6;
long long int v[N];
int main(){int n,k;cin>>n>>k;for(int i=1;i<=n;i++){cin>>v[i];}long long int ans=0;for(int i=1;i<=n;i++){long long int m=v[i];//最大值long long int s=v[i];//最小值for(int j=i+1;j<=n;j++) {if(v[j]-s>k||m-v[j]>k){break;} else{
// cout<<"["<<i<<","<<j<<"],"<<"最小值:"<<s<<",最大值: "<<m<<endl;ans++;
// cout<<"美味区间: "<<i<<"~"<<j<<",最小值"<<s<<",最大值"<<m<<endl;if(v[j]<s){s=v[j];}else if(v[j]>m){m=v[j];}}}}cout<<ans;return 0;
}
3.纪律问题
思路
1.每个小朋友只能有一种爱好。并且这m种爱好可以用不完!
2.相邻的不能有同种爱好 -->所以合法的状态种数:m*(m-1)的(n-1)次方
3.所有可能数:m的n次方
4.所以违法记录数量为m的n次方- m*(m-1)的(n-1)次方
算法:
快速幂
能求高次幂
快速幂代码:
快速幂
ll qmi(ll a,ll b){//计算a的b次方%p
ll ans=1;
while(b) {//指数不为0if(b&1){//指数最后一位是1 就乘上aans=(ll)ans*a%p;}b=b>>1;//修改指数a=(ll)a*a%p;//修改底数
}
return ans;
}
完整代码
/*1.每个小朋友只能有一种爱好。并且这m种爱好可以用不完! 2.相邻的不能有同种爱好 -->所以合法的状态种数:m*(m-1)的(n-1)次方 3.所有可能数:m的n次方4.所以违法记录数量为m的n次方- m*(m-1)的(n-1)次方
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const ll p=1e5+3;
ll qmi(ll a,ll b){//计算a的b次方%p
ll ans=1;
while(b) {if(b&1){ans=(ll)ans*a%p;}b=b>>1;a=(ll)a*a%p;
}
return ans;
}
int main(){ll m,n;cin>>m>>n;ll a=qmi(m,n);ll b=m*qmi(m-1,n-1)%p;ll c=(a-b+p)%p;//担心小于0(所以处理)cout<<c;return 0;
}5.组合0

末尾0的个数:
统计2,5的因子个数有多少
因为2*5=10,有几个10因子就末尾有几个0
分类
#include<bits/stdc++.h>
using namespace std;
int a2,a5;//2的个数,5的个数
int f2(int a){//计算2个数
int cnt=0; while(a%2==0){cnt++;a/=2; }return cnt;
}
int f5(int a){int cnt=0;while(a%5==0){cnt++;a/=5;}return cnt;
}
void cal(int n,int m){//Cnm
for(int i=n;i>m;i--){a2+=f2(i);a5+=f5(i);
}
for(int i=1;i<=n-m;i++){a2-=f2(i);a5-=f5(i);
}}
int main(){int t;int n,m;cin>>t;while(t--){cin>>n>>m;a2=0;a5=0;cal(n,m);cout<<min(a2,a5)<<endl;}return 0;
}4. 蓝泽的秘密邮件
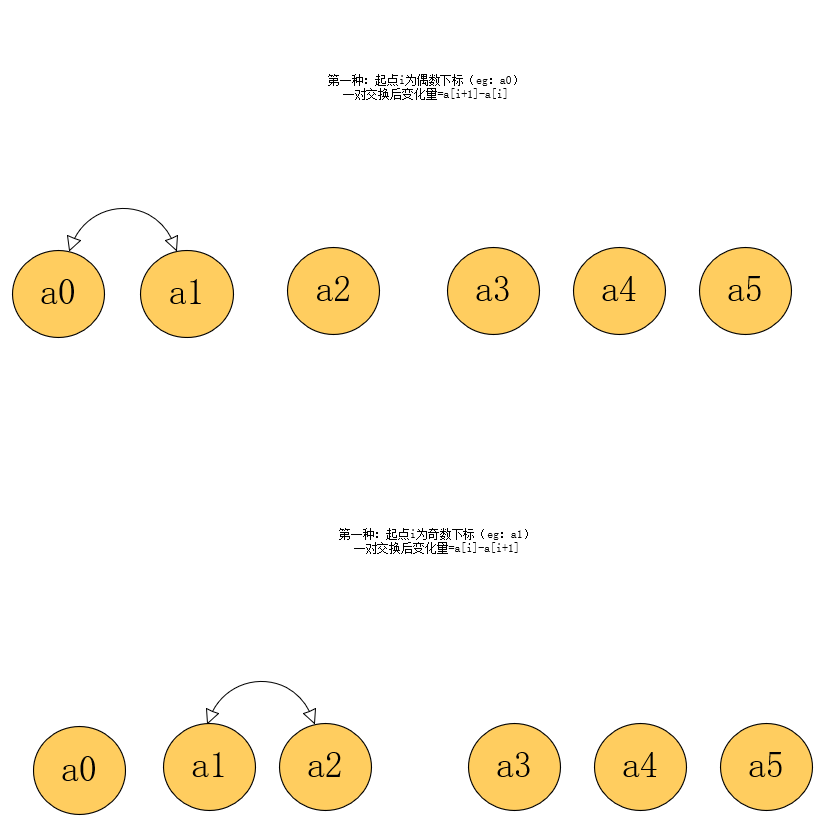
思路:
完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll check(ll a[],ll n){ll t=0;for(ll i=0;i<n;i+=2){//记录所有偶数下标对应数值的总和t+=a[i];}ll max1=0;//第一种情况起点奇数下标当前最大总和ll max2=0;//第二种情况起点偶数下标当前最大总和ll mx=0;//最大变化量总和ll j;//起点为奇数下标,交换变化 。 ll o;//偶数为起点下标,交换变化 //都是向后翻 for(ll i=0;i<n-1;i++){//不能到最后一个点 (因为有a[i+1])if(i%2==0){//起点:偶数下标o=a[i+1]-a[i];j=0; }else{//起点:奇数下标 j=a[i]-a[i+1];o=0; }max1=max(j,max1+j);//看是否需要连续,处理奇数起点。j不连续,max1+j连续max2=max(o,max2+o);//处理偶数起点mx=max(mx,max(max1,max2));//最大变化量,就是当前变化量以及奇数起点、偶数起点变化量总和最大值}return t+mx;
}
int main(){ll n;cin>>n;ll a[200006];for(ll i=0;i<n;i++){cin>>a[i];}cout<<check(a,n);return 0;
}6. 大衣好累
考点:
最大匹配问题-->能最多匹配出几对相减非0的
就是统计出最大出现次数的相同数字maxx
所以为0的对数是:zero=maxx-m
空隙数是:kx=m-zero+1
最大匹配问题
int m;cin>>m;for(int i=0;i<2*m;i++){cin>>a[i];}sort(a,a+2*m);//从小到大排序 int cnt=0;//统计当前数字相同个数 int maxx=0;//最大个数相同数字 for(int i=0;i<2*m;i++) {if(a[i]==a[i-1]){cnt++;}else{cnt=1;//至少出现1次 }maxx=max(cnt,maxx);}int zero=maxx-m;//不匹配(即相减为0),zero指的是有几对搭配为0 int kx= m-zero+1;//空隙个数,减去搭配为0的对数 +1
完整代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e3+6;
int a[N];
void solve(){int m;cin>>m;for(int i=0;i<2*m;i++){cin>>a[i];}sort(a,a+2*m);//从小到大排序 int cnt=0;//统计当前数字相同个数 int maxx=0;//最大个数相同数字 for(int i=0;i<2*m;i++) {if(a[i]==a[i-1]){cnt++;}else{cnt=1;//至少1次 }maxx=max(cnt,maxx);}int zero=maxx-m;//不匹配(即相减为0),zero指的是有几对搭配为0 int kx= m-zero+1;//空隙个数,减去搭配为0的对数 +1//0要插入到空隙里:所以当0的个数小于等于 空隙数说明可以if(kx>=zero) {cout<<"YES"<<endl;}else{cout<<"NO"<<endl;}
}
int main(){int t;cin>>t;while(t--){solve();}return 0;
}