树
1 定义
1.1 树是什么
树是一种数据结构,因为形似倒着的树而得名.
1.2 树的定义
递归定义
1.2.1 有根树的定义
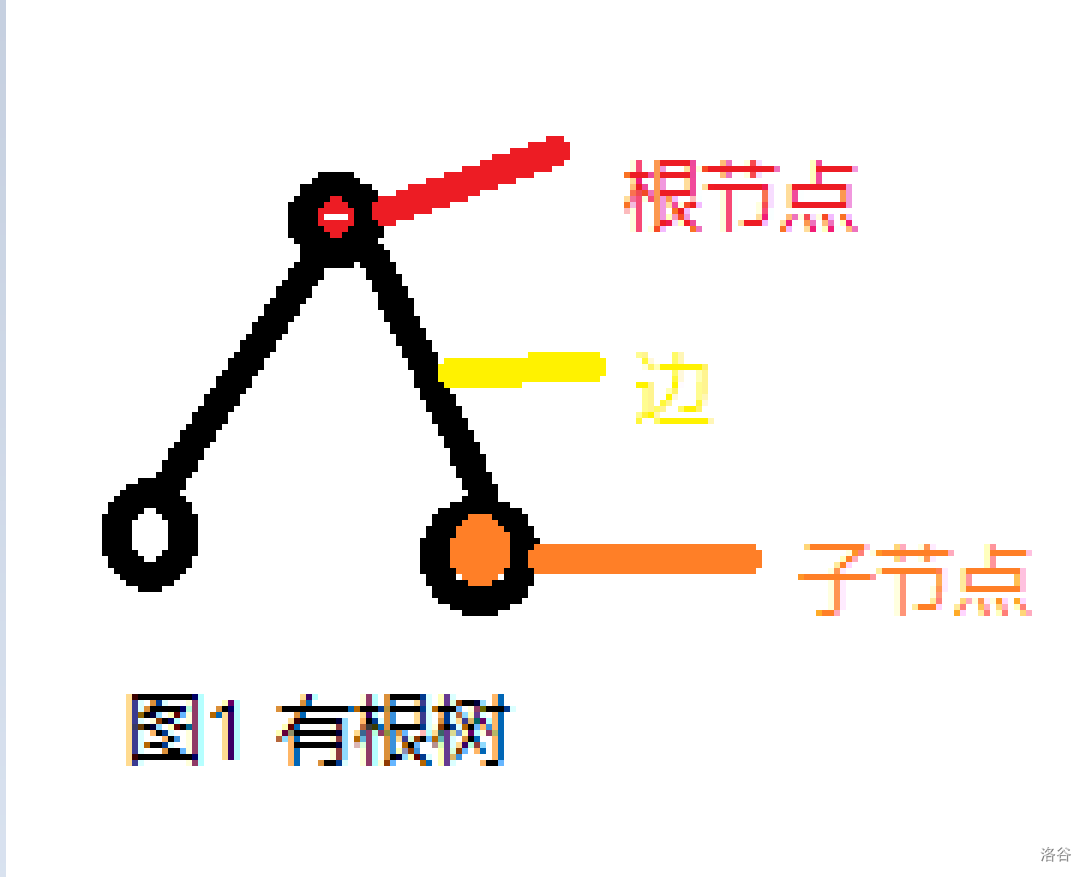
形象化的,如图1,有根树存在根节点这一定义,从根节点可以分出任意个分支,这任意个分支又可以继续细分,分出的节点称为“子节点”。
抽象化的,树也是\(N\)个节点和\(N-1\)条边的集合。
每条边都将某个节点连接至他的父亲,而除去根节点外的每个节点都有父亲,每个结点之间互不相交。
1.2.2 无根树的定义
形象化的,无根树就是有根树删去根节点后得到的东西
抽象化的,无根树也是树是\(N\)个节点和\(N-1\)条边的集合。
每条边都将某个节点连接至他的父亲,每个节点互不相交
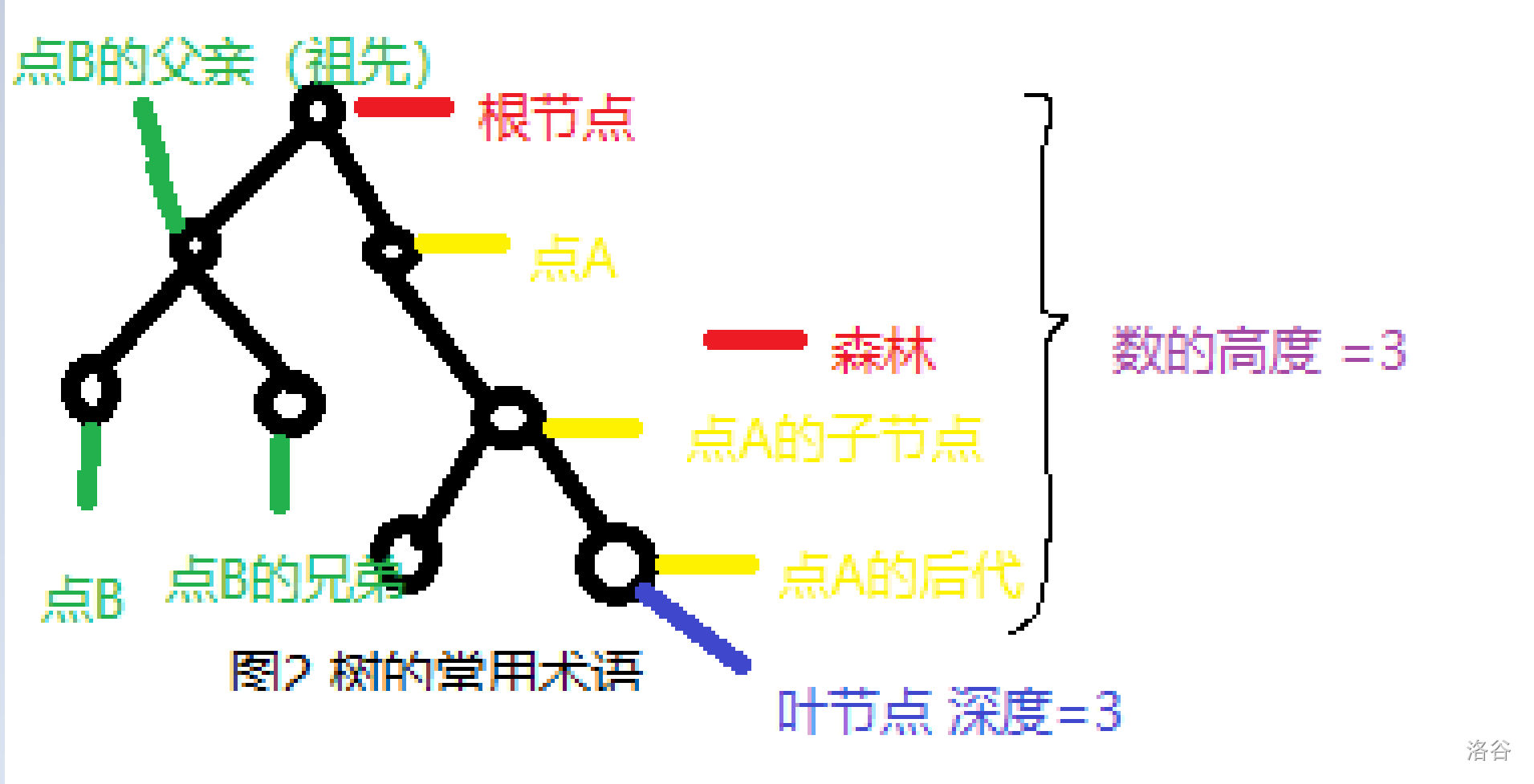
1.3 有关树的一些常用术语
森林:每个连通块都是树的图。按照定义,一棵树也是森林
叶节点:没有子节点的节点
父亲:一个节点上一层的点
祖先:一个点上层的每一个点
子节点:一个节点延伸出的下一个节点
深度:一个点到根节点的层数(边数)
高度:从叶节点到根节点的层数。
兄弟:同一个父节点的子节点互为兄弟
后代:一个点下层的每一个点是当前点的后代。
度:一个节点的子树个数(其实这个概念应该放在前面,大家可以试着使用度来概括一些前期概念)
内部节点:根以外的分支节点
树的度:这棵树各节点中度的最大值
1.4 特殊树
链:满足与任意节点相连的边不超过2条的树
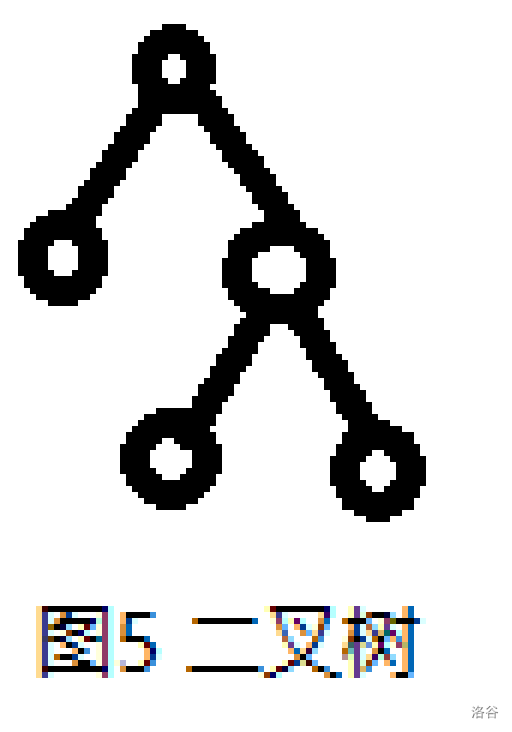
二叉树:每个节点最多只有两个子节点的树。
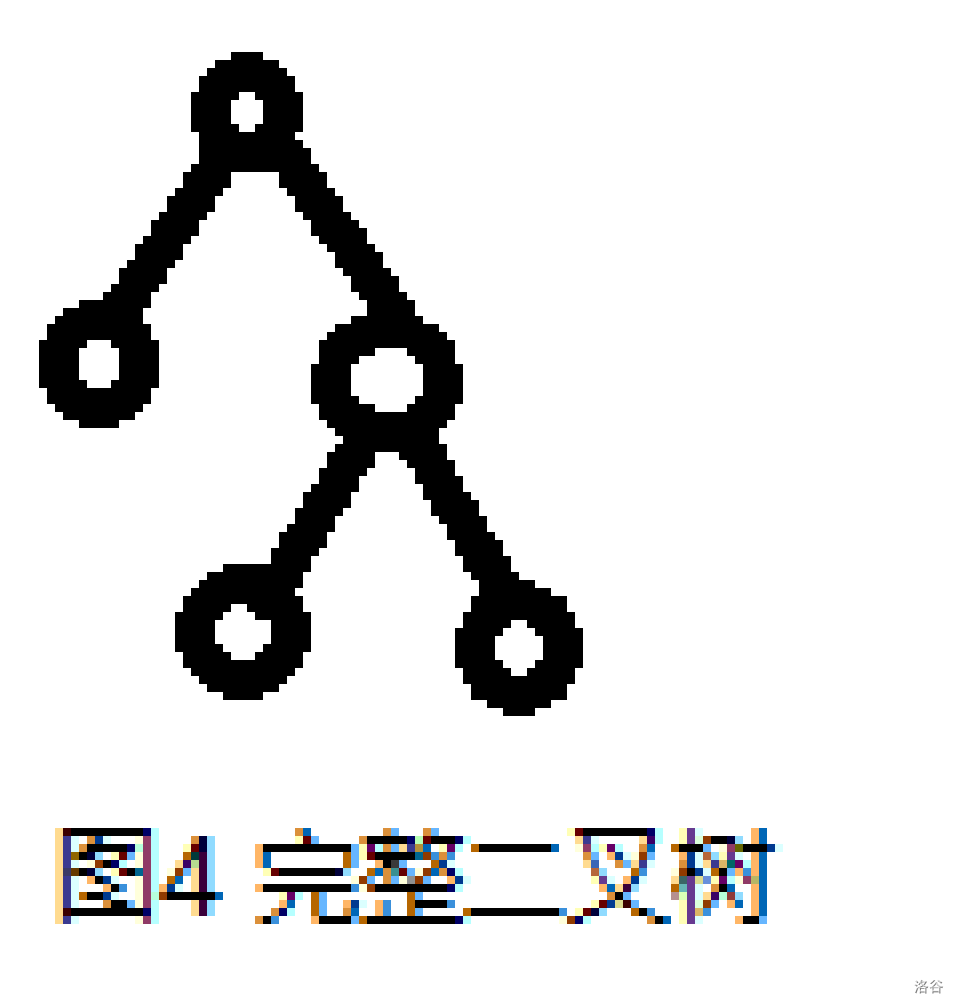
完整二叉树:每个节点的子节点数量都为2或没有
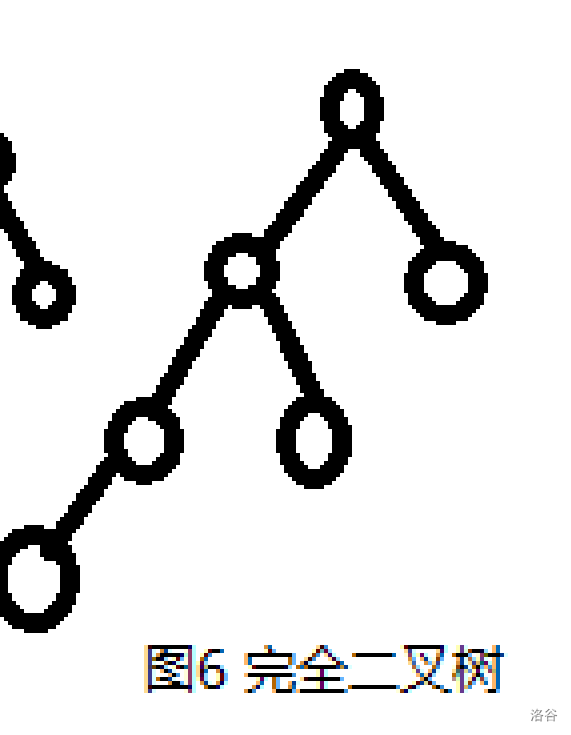
完全二叉树:只有最下面两层节点度数可以\(<2\),且最下面一层节点都位于该层最左边的位置上。
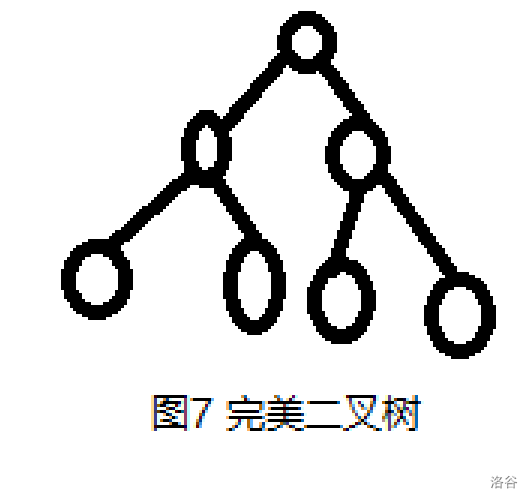
完美二叉树:所有叶节点深度相同,且所有节点都只有两个子节点!
注意!完美二叉树一定也是完全二叉树和完满二叉树,但完满二叉树不一定是完全二叉树和完美二叉树。

1.5 二叉树的一些性质
性质部分:
1.在二叉树的第\(i\)层上最多有\(2^{i-1}\)个节点
2.深度为\(k\)的二叉树最多有\(2^k-1\)个节点
3.对任意一棵二叉树,如果其叶节点数为\(n_0\),度为\(2\)的节点数为\(n_2\),则一定满足\(n_0=n_2+1\)
4.具有\(n\)个基点的完全二叉树的深度为\(floor(log_2n)+1\)
5.对于一棵\(n\)个节点的完全二叉树,对任意一个节点\(i\),有:
5.1 如果\(i=1\),则节点\(i\)为根,无父节点;
5.2 如果\(i>1\),则其父节点编号为\(i/2\)
5.3 如果\(2*i>n\),则节点\(i\)是叶节点,否则左孩子编号为\(2*i\)
5.4 如果\(2*i+1>n\),则节点\(i\)无右孩子,否则右孩子编号为\(2*1+1\)
证明部分:
用归纳法证明性质1.
当\(i=1\)时,
2 树的储存
2.1 普通树的储存
2.1.1 顺序存储
1.父亲表示法(数组记录孩子的父亲为父亲)
int data[N];//存数据的
int father[N];//father[i]=j 表示i的父亲为j
2.孩子表示法(数组记录父亲的第任意个孩子为孩子)
int data[N];//不做过多解释
int son[N][M];//son[i][j]=k表示父亲i的第j个孩子为k
3.父亲孩子表示法(双向奔赴的爱)
int data[N];//不做过多解释
int father[N];//father[i]=j 表示i的父亲为j
int son[N][M];//son[i][j]=k表示父亲i的第j个孩子为k
4.孩子兄弟表示法(见故事)
int data[N];//不做过多解释
int firstson[N];//表示父亲的第一个孩子
int nxt[N];//nxt[i]=j表示i的下一个兄弟为j
这里我们老师给我们讲了个故事,说乾隆生了100多个孩子,这时候怎么记是不是自己孩子呢?就让哥哥记住自己弟弟,弟弟在记住自己弟弟,这就是孩子兄弟表示法。
2.1.2 链式存储
1.父亲表示法
struct node
{int data;// 节点存储的数据node *father// 指向父节点的指针
}tree[N];//树
2.孩子表示法
struct node
{int data;// 节点存储的数据node *son[M];//指向子节点的指针
}tree[N];
3.父亲孩子表示法
struct node
{int data;//数据node *father;//指向父亲node *son[M];//指向孩子
}tree[N];
4.孩子兄弟表示法
struct node
{int data;//数据node *firstson;//第一个儿子node *bro;//下一个兄弟
}tree[N];
2.2 二叉树的存储
1.顺序存储
int data[N];//数据域
2.链式存储
struct node
{int data;node *lc;//左孩子node *rc;//右孩子node(int d)//构造函数{data=d;// 初始化节点数据为传入的参数dlc=NULL;// 初始化左子节点指针为NULLrc=NULL;// 初始化右子节点指针为NULL}//另一种写法/*node(int d) : data(d), lc(NULL), rc(NULL){}*/
};
node *bt;//根节点指针
3.树的遍历
先序遍历,中序遍历,后序遍历
3.1 先序遍历
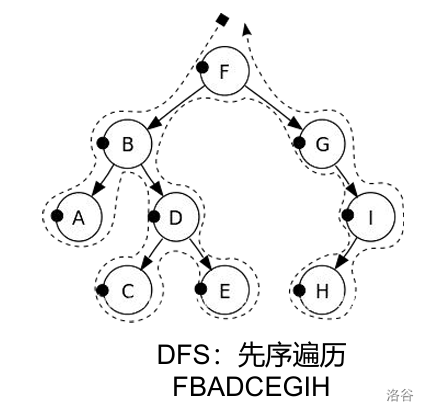
如图8,先序遍历类似\(DFS\),从根开始,然后是左子树,递归到最深层后返回,然后遍历右子树,最后回到根
void preoder(int f)
{cout<<data[f]<<" ";//首先在函数运行前输出是为了先从根节点开始if(lc[2*f]>0)//左子树preoder(2*f);if(rc[2*f+1]>0)//右子树preoder(2*f+1);
}
3.2 中序遍历
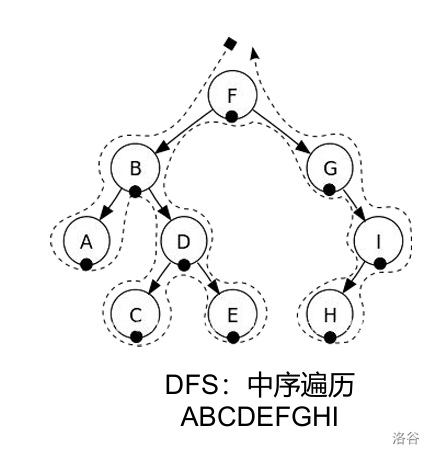
如图9,中序遍历在遍历完左子树后直接跳向根节点后遍历右子树
void inoder(int f)
{if(lc[f]>0)inoder(lc[f]);cout<<data[f]<<endl;//在遍历左子树时输出是为了先从左子树开始if(rc[f]>0)inoder(rc[f]);
}
3.3 后序遍历
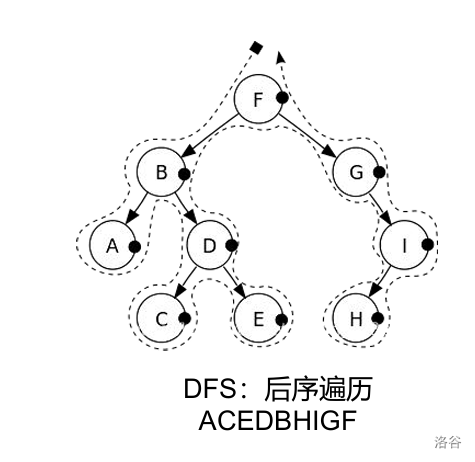
如图10,后序遍历在遍历完左子树后直接跳向右子树叶子节点后向上遍历至根节点
void postoder(int f)
{if(lc[f]>0)postoder(lc[f])if(rc[f]>0)postoder(rc[f]);cout<<data[f]<<endl;//在遍历右子树时输出是为了从右子树开始
}
3.4 FAQ
肯定会有彭于晏有疑问,为什么他们的输出位置不同,决定了他们的遍历次数不同?
1.先序遍历 首先在函数运行前输出是为了先从根节点开始
2.中序遍历 在遍历左子树时输出是为了先从左子树开始
3.后序遍历 在遍历右子树时输出是为了从右子树开始
神不神奇?反正我觉得挺神奇
接下来需要完善的:
2.二叉树性质 证明
4.反推
5.BFS
6.Morris
呼~~ 用时7个多小时终于写完了!希望能帮到你喵~~