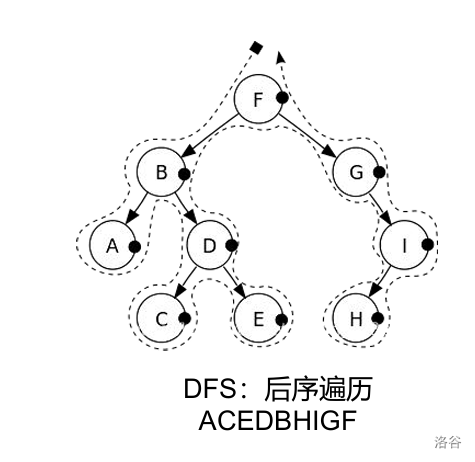
A
签到题,没啥可说的
#include<iostream>
#include<cstring>
using namespace std;const int N = 110;int n,m;
int x[N],y[N];void solve() {memset(x, 0, sizeof(x));memset(y, 0, sizeof(y));for(int i = 1; i <= n;i++) {cin>>x[i]>>y[i];}int sum1 = 0, sum2 = 0;for(int i = 1; i <= n; i++) {sum1 += x[i];x[i] = sum1;sum2 += y[i];y[i] = sum2;}pair<int,int>zuoshang;zuoshang.first = sum1;zuoshang.second = sum2 + m;pair<int,int>youxia;youxia.first = sum1 + m;youxia.second = sum2;int l = youxia.first - x[1];int r = zuoshang.second - y[1];int ans = l * 2 + r * 2;cout<<ans<<endl;
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t;cin>>t;while(t--) {cin>>n>>m;//n 是次数,m是lengthsolve(); }return 0;
}
B
- 网上有人说是拓扑排序,我这里是直接从小到大检索,有几个比他小就说明后面要多空几个位置。
#include<iostream>
#include<cstring>
using namespace std;const int N = 1e3 + 10;int n;
int g[N][N];
string s[N];
int ans[N];
bool str[N];void solve() {memset(str, false, sizeof(str));memset(g, 0, sizeof(g));memset(ans, 0, sizeof(ans));cin>>n;for(int i = 1; i <= n; i++) {cin>>s[i];}for(int i = 1; i <= n; i++) {for(int j = 0; j < i - 1; j++) {if(s[i][j] == '1') {s[i][j] = '0';}}}memset(str, false, sizeof(str));for(int i = 1; i <= n; i++) {int ant = 0;for(int j = 0; j < n; j++) {if(s[i][j] == '1') {ant++;}}int num = 0;for(int k = n - ant + 1; k <= n; k++) {if(!str[k]) {num++;}}for(int k = n - ant; k >= 1; k--) {if(!str[k] && num == ant) {str[k] = true;ans[k] = i;break;}if(!str[k]) {num++;}}}
// 1
//3
//000
//001
//010
//3 2 1for(int i = 1; i <= n ; i++) {cout<<ans[i]<<" ";}cout<<endl;}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t;cin>>t;while(t--) {solve();}return 0;
}C
- 简化问题后,就是只要我们保持最长为3,个数就是每增加一个字符,个数增加两个就ok
- 我们发现就是1 2 X X 1 2 会发现1 X 1或者2 X 2每插入一个数字就会长度为3的两个个回文串,只要保证我们插入的XX相异即可。
#include<iostream>
#include<cstring>
using namespace std;const int N = 1e3 + 10;int n;
//个数增多,但是不能增长 void solve() {cin>>n;if(n == 6) {cout<<"1 1 2 3 1 2"<<endl;return;}for(int i = 1; i <= n - 2; i++) {cout<<i<<" "; }cout<<"1 2"<<endl;
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t;cin>>t;while(t--) {solve();}return 0;
}搜索
import java.util.Scanner;public class Main {static final int N = 110;static int n, m;static String[] s = new String[N];static int[][] g = new int[N][N];static boolean[][] str = new boolean[N][N];static int[] dx = {1, 0, -1, 0};static int[] dy = {0, 1, 0, -1};public static void dfs(int x, int y) {for(int i = 0; i < 4; i++) {int nowx = x + dx[i];int nowy = y + dy[i];if(!str[nowx][nowy] && g[nowx][nowy] != 0) {str[nowx][nowy] = true;dfs(nowx, nowy);}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();for(int i = 1; i <= n; i++) {s[i] = scanner.next();}for(int i = 1; i <= n; i++) {for(int j = 0; j < m; j++) {g[i][j + 1] = s[i].charAt(j) - '0';}}int ans = 0;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(g[i][j] != 0 && !str[i][j]) {str[i][j] = true;dfs(i, j);ans++;}}}System.out.println(ans);return;}
}
#include<iostream>
#include<cstring>
using namespace std;const int N = 1e2 + 10;
int n,m;
string s[N];
int g[N][N];
bool str[N][N];
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};void dfs(int x, int y) {for(int i = 0; i < 4; i++) {int nowx = x + dx[i];int nowy = y + dy[i];if(!str[nowx][nowy] && g[nowx][nowy] != 0) {str[nowx][nowy] = true;dfs(nowx, nowy);}}
}int main() {ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin>>n>>m;for(int i = 1; i <= n; i++) {cin>>s[i];}for(int i = 1; i <= n; i++) {for(int j = 0; j < m; j++) {g[i][j + 1] = s[i][j] - '0';}}int ans = 0;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(g[i][j] != 0 && !str[i][j]) {str[i][j] = true;dfs(i, j);ans++;}}}cout<<ans<<endl;return 0;
}