参考资料
大模型分布式训练并行技术(五)-序列并行
详解MegatronLM序列模型并行训练(Sequence Parallel)
一、序列并行(Colossal-AI)背景
Colossal-AI 序列并行诞生的背景是 self-attention 的内存需求是输入长度(sequence length)的2次方。其复杂度为 \(O(n^2)\),其中,n 是序列长度。换言之,长序列数据将增加中间activation内存使用量,从而限制设备的训练能力。
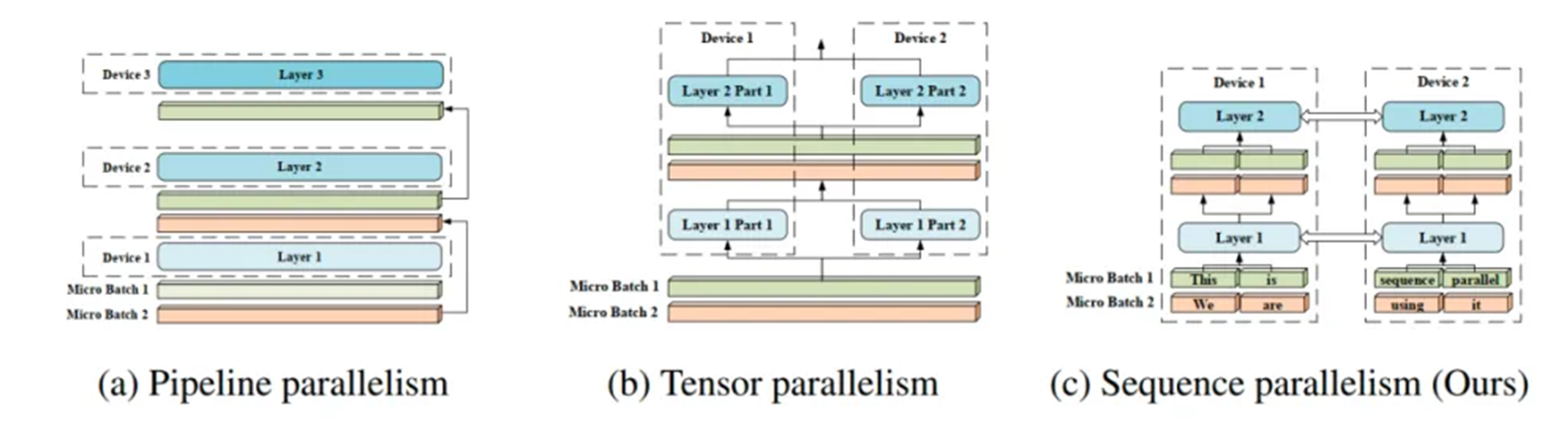
而现有的工作侧重于从算法的角度降低时间和空间复杂度。因此,作者提出了序列并行,这是一种内存高效的并行方法,可以帮助我们打破输入序列长度限制,并在 GPU 上有效地训练更长的序列;同时,该方法与大多数现有的并行技术兼容(例如:数据并行、流水线并行和张量并行)。
更重要的是,我们不再需要单个设备来保存整个序列。即在稀疏注意力的情况下,我们的序列并行使我们能够训练具有无限长序列的 Transformer。
二、模型构成
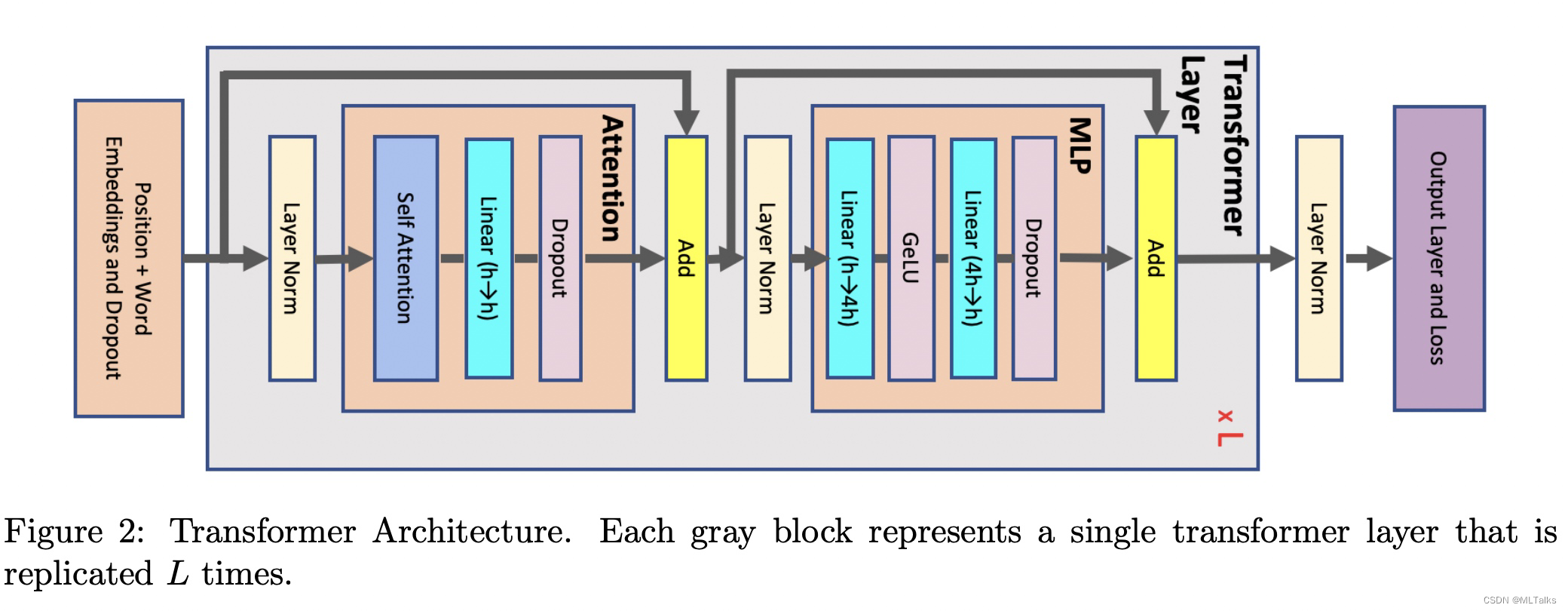
一个Transformer块中由一个Attention块和一个MLP块组成,中间通过两个LayerNorm层进行连接。在Transformer中用到的参数表示如下:
1、self-Attention 模块的计算公式如下:
Variable names :
a : number of attention heads
b : microbatch size
h : hidden dimension size
L : number of transformer layers
p : pipeline parallel size
s : sequence length
t : tensor parallel size
v : vocabulary size
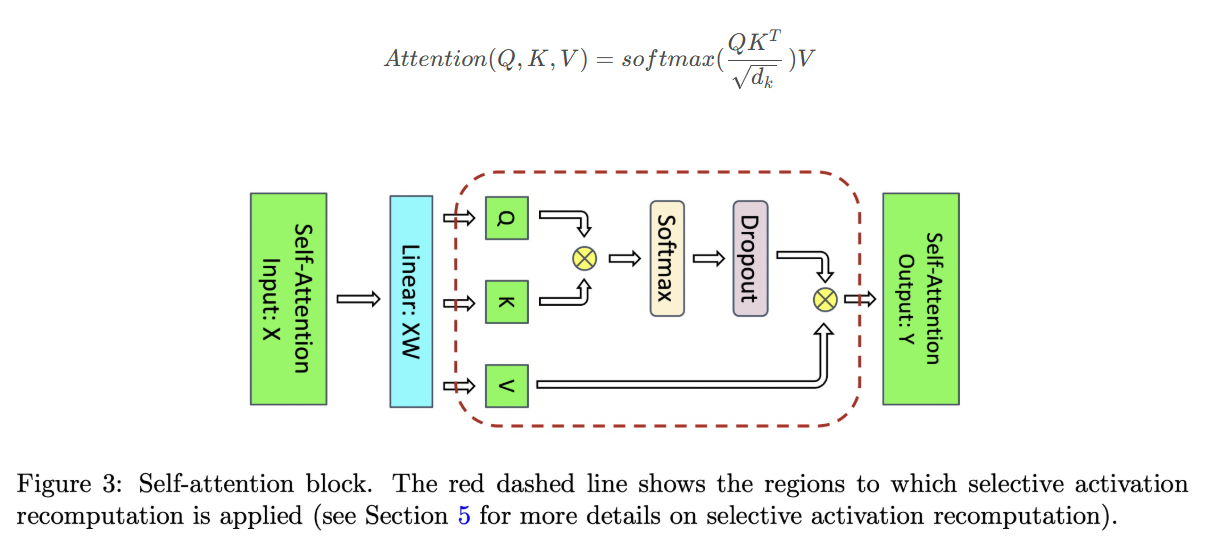
对于Attention块来说,输入的element个数为sbh个,每个element以16-bit的浮点数(也就是2 bytes)来进行存储的话,对应输入的element大小为2sbh bytes,后续计算默认都是按bytes为单位进行计算。
Attention块中包含一个self-attention块、一个linear线性映射层和 attention dropout层。
(1) 对于linear线性映射层来说需要保存输入的Activation大小为2sbh,
(2) 对于attention dropout层需要mask的大小为sbh(对于一个元素的mask只用1个bytes即可),
(3) 对于self-attention块的Activation Memory的计算有以下几块:
Query(Q), Key(K),Value(V) 矩阵相乘:
-
输入input是共享的,元素个数为sbh个,总大小是 2sbh bytes。
-
$ QK^T$ 矩阵相乘:需要分别创建保存 Q 和 K 的矩阵,每个矩阵元素总大小为 2sbh bytes, 总共大小为 4sbh bytes。
如下图以 b=1, s=2, h=6 为例,输入 X 元素个数为 1 * s * h = 12个,计算完后 Q 和 K 的矩阵中元素个数各有 1 * s * h = 12个,总元素大小为2 * 2 * b * s * h = 48 bytes。
b : microbatch size
s : sequence length
h : hidden dimension size
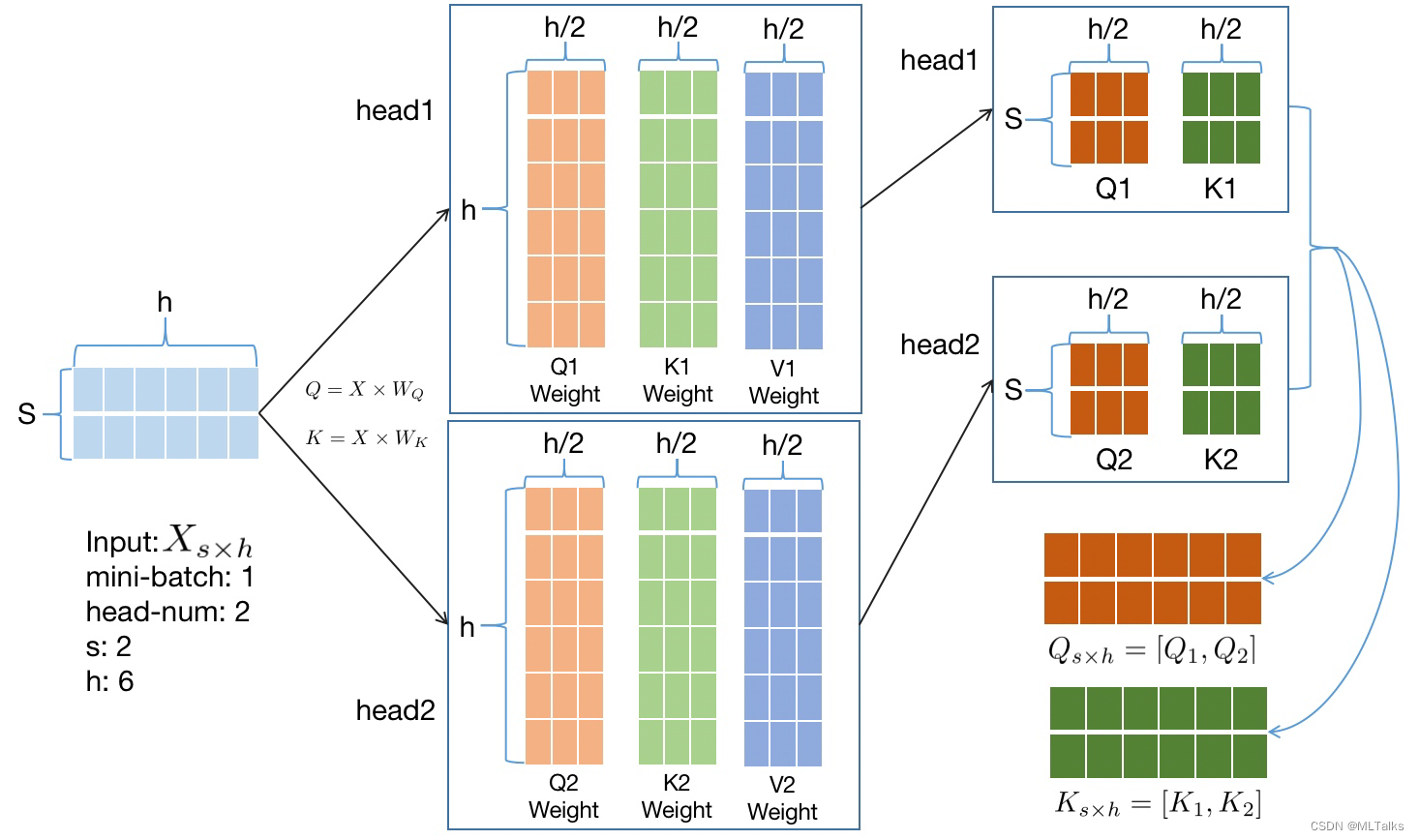
softmax 的输出总的元素大小为 \(2as^2b\) bytes, 分别计算每个Head头的的乘积 \(Q_n * K_n\)。计算公式如下, 图中计算以 b=1, s=2, h=6, a=2 为例:
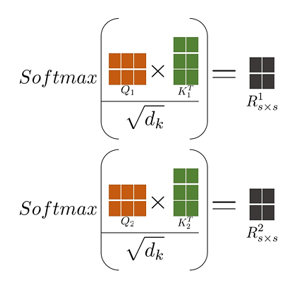
(4)在softmax后还有dropout的mask层大小,mask矩阵的大小与softmax的输出一样,元素个数都是 $as^2b $ 个,但mask单个元素的大小只用1 bytes即可,总的大小为 $as^2b $ bytes。
(5)softmax的输出也会用于反向的计算,需要缓存下来,对应大小也是 $2as^2b $
(6)V 矩阵的大小之前没有统计,和 Q、K 矩阵一样,大小也是2sbh bytes。
综上,Attention Block 总的大小为 \(11sbh + 5as^2b\) bytes。
2、MLP 层
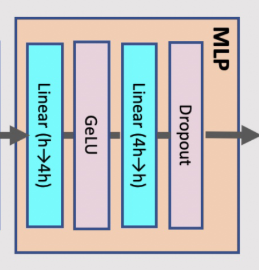
MLP 的Activation大小计算:
-
MLP中有两层线性layer,分别存储输入矩阵大小为2sbhbytes和8sbhbytes; -
GeLU的反向也需要对输入进行缓存,大小为8sbhbytes; -
dropout层需要sbhbytes;
总大小为 19sbh。
3、LayerNorm 层
LayerNorm 的 Activation大小计算:
每个LayerNorm层的输入需要 2sbh 大小,有两个LayerNorm层,总大小为 4sbh bytes.
最终transformer网络中一层(含Attention/MLP/LayerNorm)的Activation总的大小为:
注意: 这里公式(1)计算的Activation总和是在没有应用模型并行策略的前提下进行的。
三、优化模型
1、Tensor 并行
如下图,在 Tensor 模型并行中只在 Attention 和 MLP两个地方进行了并行计算,对于Attention(Q/K/V)和MLP(Linear Layer)的输入并没有并行操作。
图中 f 和 $ \overline{f} $ 互为共轭(conjugate),f 在前向时不做操作,反向时执行all-reduce,$ \overline{f} $ 在前向时执行 all-reduce, 反向时不做操作。
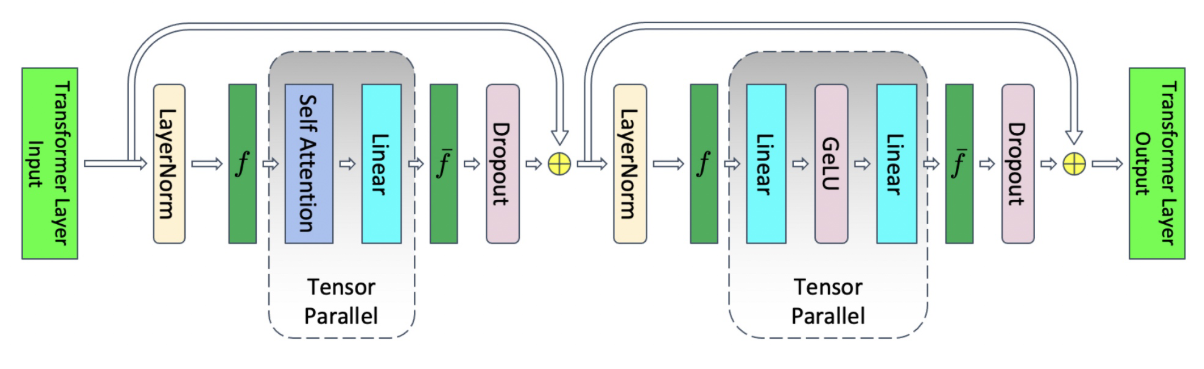
参虑上Tensor并行的话(Tensor并行度为 t),并行部分有 MLP 的 Linear部分18sbh bytes 和 Attention 的 QKV 部分(6sbh bytes), ActivationMemoryPerLayer 相比公式(1)中的值降为:
2、Sequence Parallel 序列并行
在Tensor模型并行基础上提出了Sequence Parallel,对于非Tensor模型并行的部分在sequence维度都是相互独立的,所以可以在sequence维度上进行拆分(即sequence parallel)。
拆分后如下图,f 和 $ \overline{f} $ 替换为 g 和 \(\overline{g}\), g 和 \(\overline{g}\) 也是共轭的,g 在前向是 all-gather 通信,反向是reduce-scatter通信;\(\overline{g}\) 在前向是 reduce-scatter, 反向是 all-gather 通信。
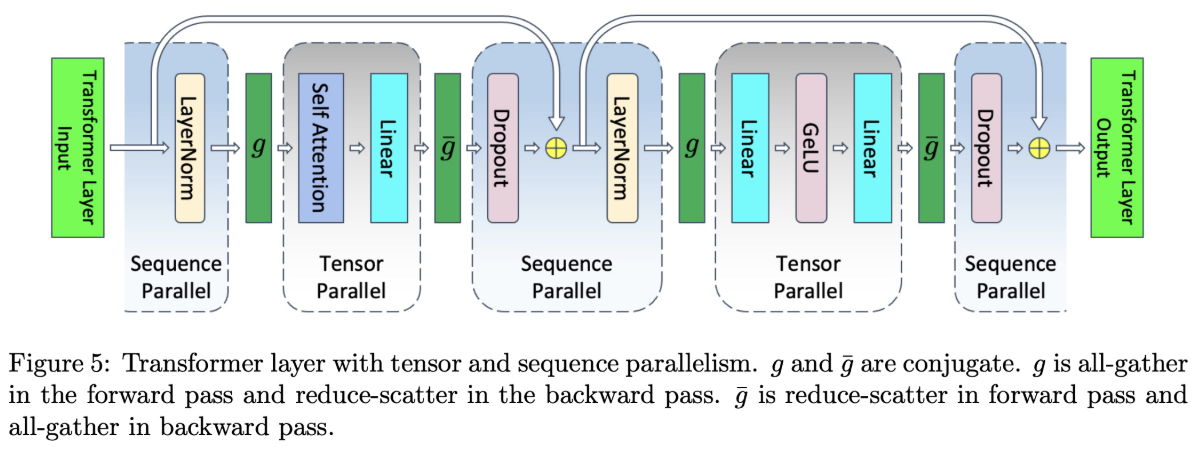
3、NLP 拆分
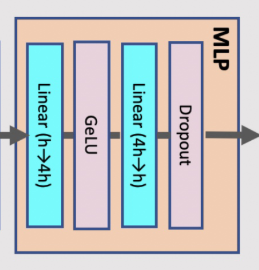
接下来以MLP为例,详细说明拆分步骤。MLP层由两个Linear层组成,对应的计算公式如下:
Y = LayerNorm(X)
Z = GeLU(YA)
W = ZB
V = Dropout(W)
其中 X 的大小为 s × b × h ; A 和 B是 Linear 的权重 weight 矩阵,大小为 h × 4 h 和 4 h × h。
1、对 X 按sequence维度切分,X = [\(X^s_1\) , \(X^s_2\)] ,LayerNorm的结果 Y = [\(Y^s_1\) , \(Y^s_2\)]
2、由于接下来的GeLU不是线性的,所以要进行all-gather操作,计算 Z=GeLU(YA);
3、对 A 进行列切分的tensor并行,得到结果 \(YA^c_1\) 和 \(YA^c_2\)
4、对 B 进行行切分的tensor并行,得到结果 \(Z^h_1 B^r_1\) 和 \(Z^h_2 B^r_2\)
5、得到 \(W_1\) 和 \(W_2\) 后进行累加操作(reduce-scatter)
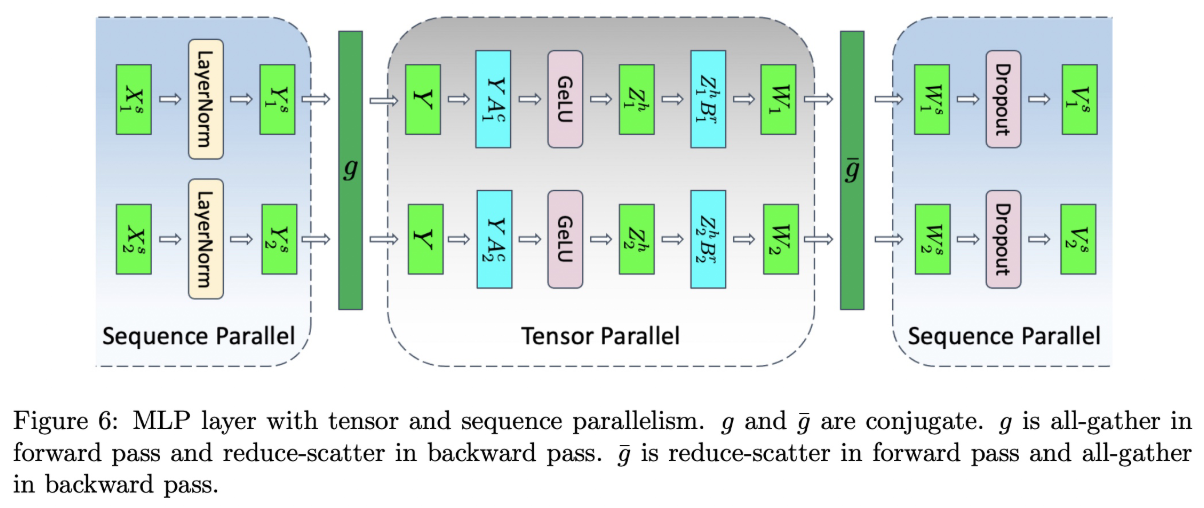
[\(Y^s_1\) , \(Y^s_2\)] = LayerNorm([\(X^s_1\) , \(X^s_2\)])
Y = g(\(Y^s_1\) , \(Y^s_2\))
[\(Z^h_1\), \(Z^h_2\)] = [GeLU(\(YA^c_1\)), GeLU(\(YA^c_2\))]
\(W_1\) = \(Z^h_1 B^r_1\)
\(W_2\) = \(Z^h_2 B^r_2\)
[\(W^8_1\), \(W^8_2\)] = \(\overline{g}\) (\(W^8_1\), \(W^8_2\))
[\(V^8_1\), \(V^8_2\)] = [Dropout(\(W^8_1\)), Dropout(\(W^8_2\))]
Tensor并行在一次前向和后向总共有4次的all-reduce操作,在Sequence并行一次前向和后向总共有4次all-gather和4次reduce-scatter操作。ring all-reduce 执行过程中有两步,先是一个reduce-scatter然后跟着一个all-gather,Sequence并行相比没有引入更多的通信代价。
4、重计算
通过对Transformer层中所有Activation的消耗进行计算,发现在Transformer层里有一些操作是产生的激活值大,但计算量小。因此,就考虑干掉这一部分的激活值,通过选择性的进行激活重新计算(Selective Activation Recomputation)来进一步降低显存。与此同时,其他的激活值就通通保存,以节省重计算量。
通过对激活值的占比分析,序列并行降低了4成左右的激活值开销。选择性激活重新计算(selective activation recompute)也降低了4成左右的激活值开销。当两个特性都打开的时候,总共可以降低8成左右的激活值开销,尽管比全部激活值重计算的结果要稍高,但是在吞吐率上的提升还是非常的明显的。