动力学研究物体的运动和作用力之间的关系。机器人动力学问题有两类:一是已知机器人各关节的驱动力或力矩,求解机器人各关节的位置、速度和加速度,这是动力学正问题;二是已知各关节的位置、速度和加速度,求各关节所需的驱动力或力矩,这是动力学逆问题。机器人的动力学正问题主要用于机器人的运动仿真。例如在机器人设计时,需要根据连杆质量、运动学和动力学参数、传动机构特征及负载大小进行动态仿真,从而决定机器人的结构参数和传动方案,验算设计方案的合理性和可行性,以及结构优化的程度;在机器人离线编程时,为了估计机器人高速运动引起的动载荷和路径偏差,要进行路径控制仿真和动态模型仿真。研究机器人动力学逆问题的目的是为了对机器人的运动进行有效的实时控制,以实现预期的轨迹运动,并达到良好的动态性能和最优指标。由于机器人是个复杂的动力学系统,由多个连杆和关节组成,具有多个输入和多个输出,存在着错综复杂的耦合关系和严重的非线性,所以动力学的实时计算很复杂,在实际控制时需要做一些简化假设。
1、机械臂连杆受力分析
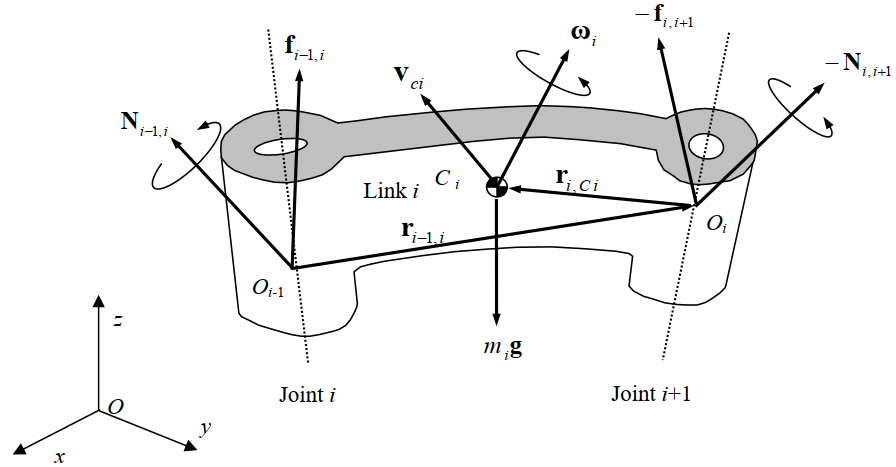
机器人连杆$i$的两端是关节$i$和关节$i+1$,杆$i$的两端分别有坐标系$i-1$和坐标系$i$的原点$O_{i-1}$和$O_i$,以及作用于杆$i$的外力(参考下图)有:
①杆$i-1$作用到杆$i$上的力系。此力系可向$O_{i-1}$点简化为一个力$f_{i-1,i}$和一个力矩$N_{i-1,i}$.
②杆$i$作用到杆$i+1$上的力系可向$O_i$点简化为力$f_{i,i+1}$和力矩$N_{i,i+1}$,因此杆$i+1$作用到杆$i$上的是$f_{i,i+1}$和$N_{i,i+1}$的反作用力$-f_{i,i+1}$和$-N_{i,i+1}$(对于末端不与环境接触的自由运动机器人,该力和力矩为0).
③杆$i$上所受的重力$m_ig$
2、牛顿-欧拉法建立动力学方程
刚体运动 = 质心的平动 + 绕质心的转动。其中,质心平动用牛顿方程描述;绕质心的转动用欧拉方程描述。牛顿-欧拉法是一种递推方法,基于牛顿第二定律和欧拉方程,分别描述刚体的平动和转动动力学。它分为两个阶段:
-
前向递推:从基座到末端,计算每个连杆的速度和加速度。
-
反向递推:从末端到基座,计算每个连杆的力和力矩。
如下图所示$v_{ci}$是连杆$i$的质心$c_i$在$O_{xyz}$参考系下的线速度,惯性力为$-m_i\dot{v}_{ci}$ 。根据达朗贝尔原理(在质点运动的每一瞬时,作用于质点上的主动力、约束力和质点的惯性力组成一平衡力系。值得注意的是,质点上只作用有主动力和约束力,质点的惯性力并不作用在质点上,质点并非处于平衡状态):
$$f_{i-1,i}-f_{i,i+1}+m_ig-m_i\dot{v}_{ci}=0, \qquad i=1,...,n$$
根据欧拉方程,描述杆$i$绕其质心转动的方程为:$I_i\dot{\omega}_i+\omega_i\times I_{i}\omega_i=M_{i}$,式中$I_{i}$为杆$i$对其质心的惯性张量矩阵,$M_{i}$为作用在杆$i$上的外力系对杆$i$质心的主力矩。若$r_{i,ci}$为杆$i$质心在系$i$中的矢径,则欧拉方程可以展开为: $$N_{i-1,i}-N_{i,i+1}-(r_{i-1,i}+r_{i,ci})\times f_{i-1,i}+(-r_{i,ci})\times (-f_{i,i+1})-I_i\dot{\omega}_i-\omega_i\times (I_i\omega_i)=0,\qquad i=1,...,n$$
由于机器人末端连杆的负载是已知量,且力和力矩是由上编号连杆向下编号连杆传递的,所以在计算各连杆的力和力矩时,可以从末端$n$号连杆开始,利用上面的牛顿欧拉方程逐号向内递推计算,得到每个连杆的$f$和$N$。对于在自由空间移动的机器人来说,可以令$f_{n,n+1}$和$N_{n,n+1}$为零,所以第一次递推计算很简单。如果机器人和环境接触,在力的平衡时可能包括了由于这种接触所受的力和力矩,这时$f_{n,n+1}$和$N_{n,n+1}$就不是零了。
对于如下图所示的二连杆机构,连杆的运动被限制在平面内,因此其转动只能绕垂直于该平面的轴进行。这意味着转动轴的方向是固定的,且只有一个自由度。在三维空间中,惯性张量是一个 的矩阵,描述了物体绕不同轴的转动惯量。对于下图所示的平面连杆机构,惯性张量可以简化为一个标量$I$,欧拉动力学方程化简为$\tau=I\alpha$(此时$\omega\times I\omega=0$)。因此,连杆1的牛顿欧拉方程为:$$f_{0,1}-f_{1,2}+m_1g-m_1\dot{v}_{c1}=0 \\N_{0,1}-N_{1,2}+r_{1,c1}\times f_{1,2}-r_{0,c1}\times f_{0,1}-I_1\dot{\omega}_1=0$$
对于连杆2有:$$f_{1,2}+m_2g-m_2\dot{v}_{c2}=0 \\N_{1,2}-r_{1,c2}\times f_{1,2}-I_2\dot{\omega}_2=0$$
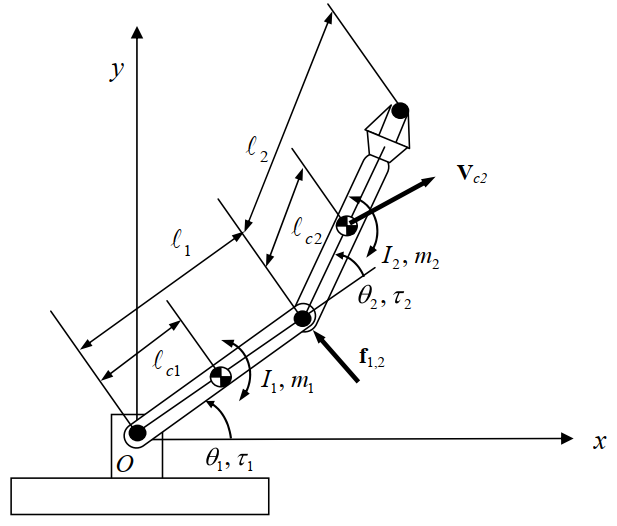
对于平面二连杆机构,关节驱动力矩$\tau_1$和$\tau_2$与上面式子中的$N$相等,即$N_{i-1,i}=\tau_i,\quad i=1,2$,消除$f_{1,2}$变量可得到:$$\tau_2-r_{1,c2}\times m_2\dot{v}_{c2}+r_{1,c2}\times m_2g-I_2 \dot{\omega}_2=0$$
同样的消除变量$f_{0,1}$后得到:$$\tau_1-\tau_2-r_{0,c1}\times m_1\dot{v}_{c1}-r_{0,1}\times m_2\dot{v}_{c2}+r_{0,c1}\times m_1g+r_{0,1}\times m_2g-I_1\dot{\omega}_1=0$$
接下来用关节角$\theta_1$和$\theta_2$来表示线速度$v_{ci}$、角速度$\omega_i$和$r_{i,i+1}$。注意$\omega_2$是相对于基坐标系的角速度(角速度的叠加遵循矢量加法规则),而$\theta_2$是相对于连杆1的角度。因此有$$\omega_1=\dot{\theta}_1,\omega_2=\dot{\theta}_1+\dot{\theta}_2$$
两个连杆质心的线速度可以写为$$v_{c1}=\begin{pmatrix}-l_{c1}\dot{\theta}_1sin\theta_1 \\l_{c1}\dot{\theta}_1cos\theta_1\end{pmatrix},v_{c2}=\begin{pmatrix}-(l_1sin\theta_1+l_{c2}sin(\theta_1+\theta_2))\dot{\theta}_1-l_{c2}sin(\theta_1+\theta_2)\dot{\theta}_2 \\(l_2cos\theta_1+l_{c2}cos(\theta_1+\theta_2))\dot{\theta}_1+l_{c2}cos(\theta_1+\theta_2)\dot{\theta}_2\end{pmatrix}$$
将角速度和质心线速度的表达式代入上面力矩的等式中,可以得到封闭形式的动力学方程,即将关节力矩和力写成关节位移、速度、加速度$(\theta,\dot{\theta},\ddot{\theta})$的显函数形式。封闭形式的动力学方程是一种以显式、解析的方式描述机器人动力学行为的数学表达式,它能够精确地刻画机器人各关节的运动与所受外力和力矩之间的关系,无需进行迭代或数值逼近计算即可得到解析解。$$\begin{align*}&\tau_1=H_{11}\ddot{\theta}_1+H_{12}\ddot{\theta}_2-h\dot{\theta}_2^2-2h\dot{\theta}_1\dot{\theta}_2+G_1\\&\tau_2=H_{22}\ddot{\theta}_2+H_{21}\ddot{\theta}_1+h\dot{\theta}_1^2+G_2\end{align*}$$
其中,$$\begin{align*}&H_{11}=m_1l_{c1}^2+I_1+m_2(l_1^2+l_{c2}^2+2l_1l_{c2}cos\theta_2)+I_2\\&H_{22}=m_2l_{c2}^2+I_2\\&H_{12}=m_2(l_{c2}^2+l_1l_{c2}cos\theta_2)+I2\\&h=m_2l_1l_{c2}sin\theta_2\\&G_1=m_1l_{c1}gcos\theta_1+m_2g(l_{c2}cos(\theta_1+\theta_2)+l_1cos\theta_1)\\&G_2=m_2gl_{c2}cos(\theta_1+\theta_2)
\end{align*}$$
可以用Mathematica计算出力矩的符号表达式:
查看代码
(*定义变量*)
r0c1={lc1 Cos[\[Theta]1[t]],lc1 Sin[\[Theta]1[t]],0};
r01={l1 Cos[\[Theta]1[t]],l1 Sin[\[Theta]1[t]],0};
r1c2={lc2 Cos[\[Theta]1[t]+\[Theta]2[t]],lc2 Sin[\[Theta]1[t]+\[Theta]2[t]], 0};
r0c2 = r01 + r1c2;
vc1=D[r0c1,t];
vc2=D[r0c2,t];
dvc1= D[vc1,t];
dvc2=D[vc2,t];
\[Omega]1={0,0,D[\[Theta]1[t],t]};
\[Omega]2={0,0,D[\[Theta]1[t]+\[Theta]2[t],t]};
d\[Omega]1 = D[\[Omega]1,t];
d\[Omega]2 = D[\[Omega]2,t];
g={0,-gy,0};
\[Tau]1 = {0,0,t1};
\[Tau]2 = {0,0,t2};(*定义力矩方程*)
e1 = \[Tau]2-r1c2 \[Cross]dvc2*m2+r1c2 \[Cross] g *m2-i2 d\[Omega]2;
e2 = \[Tau]1-\[Tau]2-r0c1\[Cross]dvc1 *m1-r01 \[Cross] dvc2 *m2+r0c1 \[Cross]g*m1+r01 \[Cross]g *m2-i1 d\[Omega]1;
eq1=e1[[3]]==0;
eq2=e2[[3]]==0;(*求解力矩表达式*)
solutions=Solve[{eq1,eq2},{t1,t2}];
\[Tau]1Expr=t1/.solutions[[1]];
\[Tau]2Expr=t2/.solutions[[1]];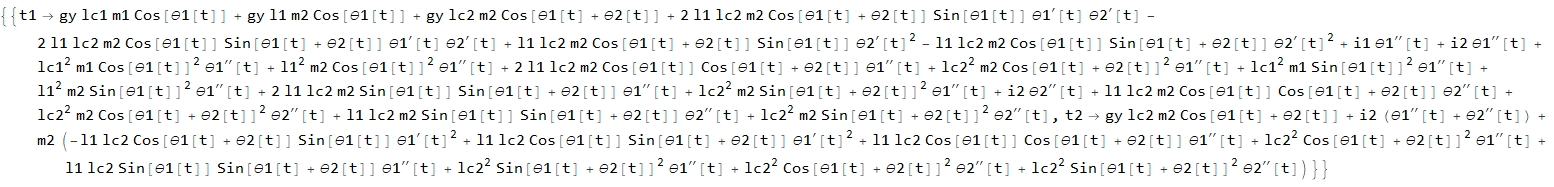
从上面的例子可以看出,机器人动力学方程的计算比较烦琐,才两个连杆,表达式看着就已经让人头大了。随着机器人自由度数增加,计算将变得更加复杂。对于$n$自由度的机器人,一般形式的封闭动力学方程可以写为:$$\boxed{\tau = M(\theta)\ddot{\theta}+C(\theta,\dot{\theta})+G(\theta)}$$
其中,$M(\theta)$为$n\times n$阶正定对称矩阵,$M(\theta)\ddot{\theta}$代表惯性力项。$M(\theta)$中的主对角线元素表示各连杆本身的有效惯量,代表给定关节上的力矩与产生的角加速度之间的关系,非对角线元素表示连杆之间的耦合惯量,即是某连杆的加速运动对另一关节产生的耦合作用力矩的度量 ;$C(\theta,\dot{\theta})$为$n\times 1$阶向心力和科氏力项,由两部分组成:其一与关节速度平方成正比,表示该关节速度产生的向心力;其二与两关节速度的乘积成正比,称为科氏力;$G(\theta)$为$n\times 1$阶的重力项,与机器人的形位$\theta$有关。惯性力项和重力项在机器人控制中特别重要,因为它们直接影响机器人系统的稳定性和定位精度。向心力和科氏力只有当机器人高速运动时才有意义,否则它们造成的误差很小。也就是说,在非高速运动情况下可以不考虑。
3、动力学方程各项的物理解释
- 重力项:动力学解的方程式中$G_1$和$G_2$表示质量为$和$m_2$的连杆绕各自关节轴产生的力矩。该值依赖于机械臂的构型,当机械臂完全沿$x$轴伸展时,重力力矩达到最大值。
- 惯性力项:首先观察方程中的第一项$H_{11}\ddot{\theta}_1$。假设连杆2相对连杆1静止不动,即$\dot{\theta}_2=0$且$\ddot{\theta}_2=0$,忽略掉重力项,则关节1的动力学方程可简化为$\tau_1=H_{11}\ddot{\theta}_1$。此时系数$H_{11}$代表连杆1和连杆2对关节1的总转动惯量。$H_{11}$中前两项$m_1l_{c1}^2+I_1$为连杆1相对关节1的转动惯量,剩下的几项$m_2(l_1^2+l_{c2}^2+2l_1l_{c2}cos\theta_2)+I_2$为连杆2相对于关节1的转动惯量。该惯量大小与连杆2的质心到关节1的距离$L$有关,距离$L$是关节角$\theta_2$的函数:$L^2=l_1^2+l_{c2}^2+2l_1l_{c2}cos\theta_2$。
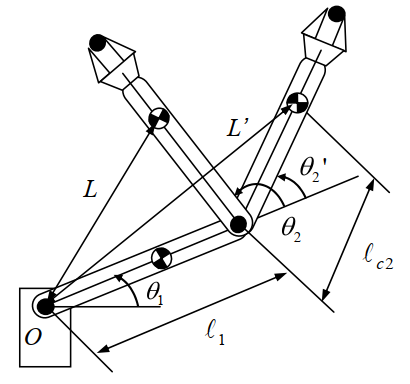
根据平行轴定理(若旋转轴平行于通过质心的轴且距离为$d$,转动惯量为:$I=I_c+md^2$。其中,$I_c$是绕质心轴的转动惯量),连杆2相对于关节1的转动惯量为$m_2L^2+I_2$。可以看到计算出的转动惯量与动力学方程中的系数$H_{11}$一致。注意转动惯量与机械臂形位有关,当二连杆机构全展开时(即$\theta_2=0$)转动惯量最大;当连杆2收回到与连杆1重合时(即$\theta_2=\pi$),转动惯量最小。
- 惯性耦合:
现在考虑动力学方程中第2项$H_{12}\ddot{\theta_2}$。假设$\dot{\theta}_1=\dot{\theta}_2=0$,且$\ddot{\theta}_1=0$,忽略掉重力项,那么第一个方程$\tau_1$可以简化为$\tau_1=H_{12}\ddot{\theta}_2$。当连杆2加速运动时,会对连杆1产生作用力和力矩。可以从受力分析中的牛顿-欧拉方程中看出,耦合力$-f_{1,2}$和力矩$-N_{1,2}$将会对连杆1的关节产生一个力矩$\tau_{int}$,将$N_{1,2}$和$f_{1,2}$的表达式带入,并设定$\dot{\theta}_1=\dot{\theta}_2=0$,及$\ddot{\theta}_1=0$可得到:
$$\begin{align*}\tau_{int}&=-N_{1,2}-r_{0,1}\times f_{1,2}\\&=-I_2\dot{\omega}_2-r_{0,c2}\times m_2\dot{v}_{c2}\\&=-(I_2+m_2(l_{c2}^2+l_1l_{c2}cos\theta_2))\ddot{\theta}_2 \end{align*}$$
这与最终动力学方程中的第2项$H_{12}\ddot{\theta}_2$一致,它表示第2个关节的加速度对第1个关节的惯性力的贡献。如果$H_{1,2}$不为零,说明第二个关节的加速度会对第一个关节产生惯性力。惯性矩阵$H$中,对角线元素$H_{i,i}$表示第$i$个关节的惯性力与其自身加速度的关系。非对角线元素$H_{i,j}$表示第$j$个关节的加速度对第$i$个关节的惯性力的耦合影响。这种耦合效应是由于机器人连杆之间的质量分布和运动学关系导致的。当第 $j$个关节加速时,它会通过连杆的质量和几何结构传递惯性力到第$i$个关节。
- 向心力(离心力)项:
向心力是由于机械臂的连杆在旋转运动中产生的惯性力。当机械臂的关节旋转时,连杆上的质量会因旋转运动而产生向心加速度,从而产生向心力。动力学方程中的第3项与关节速度成比例,假设某一时刻$\dot{\theta}_2=0$且$\ddot{\theta}_1=\ddot{\theta}_2=0$,参考下图a,这时向心力作用在连杆2上,其大小为$|f_{cent}|=m_2L\dot{\theta}_1^2$,其中$L$为连杆2的质心到第一个关节$O$的距离,向心力作用方向沿着矢量$r_{o,c2}$的方向。这个向心力会对关节2产生一个力矩$\tau_{cent}$:$\tau_{cent}=r_{1,c2}\times f_{cent}=-m_2l_1l_{c2}sin\theta_2\dot{\theta}_1^2$,这与动力学方程$\tau_2$中第3项$h\dot{\theta}_1^2$一致。因此可以认为,$h\dot{\theta}_1^2$项是由于连杆1的旋转产生的离心力效应作用于连杆2的关节处所引起的。同样的,以恒定角速度旋转关节2将会产生一个力矩$-h\dot{\theta}_2^2$作用于关节1上。
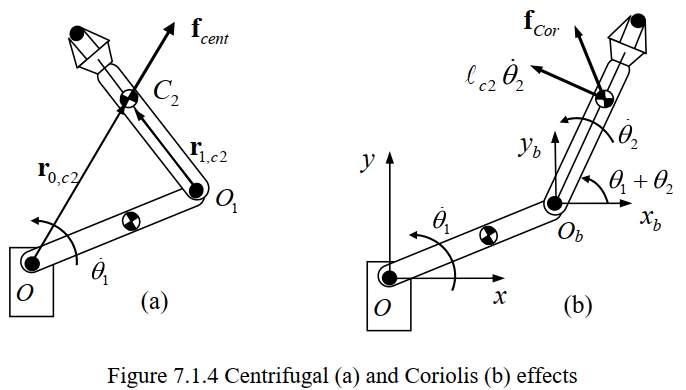
- 科氏力(科里奥利力)项
科氏力是由于机械臂的连杆在旋转参考系中具有相对运动而产生的惯性力,它反映了机械臂在运动过程中由于旋转运动和相对运动耦合而产生的惯性效应。最后来讨论动力学方程中的第4项$-2h\dot{\theta}_1\dot{\theta}_2$,它与关节速度的乘积成正比。考虑某一瞬时,二连杆机构的两个关节分别以角速度$\dot{\theta}_1$和$\dot{\theta}_2$旋转。定义一个动坐标系$O_bx_by_b$(参考图b),其原点与连杆1的末端重合,并以角速度$\dot{\theta}_1$与连杆1一起旋转,坐标系$O_bx_by_b$在该瞬时与基坐标系(静止参考系)平行。此时连杆2的质心相对连杆1(动坐标系)的相对速度大小为$v_r=l_{c2}\dot{\theta}_2$,方向与$r_{1,c2}$垂直。根据理论力学中的知识(可参考《理论力学》--高等教育出版社,谢传锋,王琪主编,5-3点的复合运动,牵连运动为定轴转动时的加速度合成定理):质点的科氏力(Coriolis Force)是由于质点在一个旋转参考系中具有相对运动而产生的惯性力。科氏力的计算需要考虑旋转参考系的角速度以及质点在旋转参考系中的相对速度。科氏力的矢量公式为:$$\boxed{\mathbf{f}_{Cor}=-2m(\boldsymbol{\omega}\times \mathbf{v}_r)}$$
其中,$m$是质点的质量,$\boldsymbol{\omega}$是旋转参考系的角速度矢量,$\mathbf{v}_r$是质点相对于旋转参考系的速度矢量。根据该公示,作用于连杆2的科氏力计算结果为:$$f_{Cor}=\begin{pmatrix}2m_2l_{c2}\dot{\theta}_2\dot{\theta}_2 cos(\theta_1+\theta_2)\\ 2m_2l_{c2}\dot{\theta}_2\dot{\theta}_2 sin(\theta_1+\theta_2)\end{pmatrix}$$
该科氏力将会对关节1产生一个力矩$\tau_{Cor}$,$\tau_{Cor}=r_{0,c2}\times f_{Cor}=2m_2l_1l_{c2}sin\theta_2\dot{\theta}_1\dot{\theta}_2$,该值与动力学方程中第4项一致。
4、拉格朗日方程
实际问题中刚体运动时往往并不是自由的,他们受到一些约束,使用牛顿-欧拉法进行受力分析时不可避免要带入约束力。而约束力是一种“被动的”力,是未知量。如果只是关心刚体的运动,求解这些约束力会增加不必要的计算量,因此希望能建立一种不含约束力的动力学方程。拉格朗日方程基于能量平衡方程,它给出了不含约束力的动力学方程。对于简单情况,运用该方法比用牛顿 欧拉方程更烦琐,然而随着系统复杂程度的增加,运用拉格朗日动力学方程将变得相对简单。所以拉格朗日动力学方程相对于牛顿 欧拉方程更适合于分析相互约束下的多个连杆运动。拉格朗日函数$L$的定义是一个机械系统的动能$K$与势能$P$之差,即$$L(\mathbf{q},\dot{\mathbf{q}})=K(\mathbf{q},\dot{\mathbf{q}})-P(\mathbf{q})$$
式中$\mathbf{q}$表示动能和势能的广义坐标,$\mathbf{q}=[q_1,q_2,...,q_n]$,$\dot{\mathbf{q}}$表示广义速度,$\dot{\mathbf{q}}=[\dot{q}_1,\dot{q}_2,...,\dot{q}_n]$。对于$n$个连杆组成的机器人,由拉格朗日函数描述的系统动力学方程为:$$\boxed{\tau_i=\frac{d}{dt}(\frac{\partial L}{\partial \dot{q}_i})-\frac{\partial L}{\partial q_i}, \quad i=1,2,...,n}$$
式中$\tau_i$为作用在第$i$个关节上的广义驱动力矩。
平面运动刚体的总动能是平动动能和转动动能之和,即$T=\frac{1}{2}mv_{ci}^2+\frac{1}{2}I_c\omega_i^2$。则二连杆机构系统总动能为:$$T=\sum_{i=1}^2(\frac{1}{2}m_iv_{ci}^2+\frac{1}{2}I_i\omega_i^2)$$
选取$\theta_1$和$\theta_2$为广义坐标,角速度可表示为$\omega_1=\dot{\theta}_1$,$\omega_2=\dot{\theta}_1+\dot{\theta}_2$。对于连杆1,其动能$K_1$ 和位能势能$P_1$为:$$\begin{align*}&K_1=\frac{1}{2}m_1(l_{c1}\dot{\theta}_1)^2+\frac{1}{2}\cdot\frac{1}{12}m_1l_1^2\cdot \dot{\theta}_1^2 \\&P_1=m_1gl_{c1}sin\theta_1 \end{align*}$$
对连杆2,其动能和势能分别为:$$\begin{align*}&K_2=\frac{1}{2}m_2v_{c2}^2+\frac{1}{2}\cdot\frac{1}{12}m_2l_2^2\cdot(\dot{\theta}_1^2+\dot{\theta}_2^2)\\&P_2=m_2gy_{c2}\end{align*}$$
由于$$ \begin{align*}&x_{c2}=l_1cos\theta_1+l_{c2}cos(\theta_1+\theta_2)
\\&y_{c2}=l_1sin\theta_1+l_{c2}sin(\theta_1+\theta_2)
\\&\dot{x}_{c2}=-l_1sin\theta_1\dot{\theta}_1-l_{c2}sin(\theta_1+\theta_2)(\dot{\theta}_1+\dot{\theta}_2)
\\&\dot{y}_{c2}=l_1cos\theta_1\dot{\theta}_1+l_{c2}cos(\theta_1+\theta_2)(\dot{\theta}_1+\dot{\theta}_2)
\end{align*}$$
所以$v_{c2}^2=\dot{x}_{c2}^2+\dot{y}_{c2}^2=l_1^2\dot{\theta}_1^2+l_{c2}^2(\dot{\theta}_1^2+2\dot{\theta}_1\dot{\theta}_2+\dot{\theta}_2^2)+2l_1l_{c2}cos\theta_2(\dot{\theta}_1^2+\dot{\theta}_1\dot{\theta}_2)$。
于是$$\begin{align*}&K_2=\frac{m_2}{24}((12l_1^2+l_2^2+12l_{c2}^2+24l_1l_{c2}cos\theta_2)\dot{\theta}_1^2+24l_{c2}(l_{c2}+l_1cos\theta_2)\dot{\theta}_1\dot{\theta}_2+(l_2^2+12l_{c2}^2)\dot{\theta}_2^2)
\\&P_2=m_2gy_{c2}=m_2gl_1sin\theta_1+m_2gl_{c2}sin(\theta_1+\theta_2)\end{align*}$$
二连杆机构的拉格朗日函数为$L=K_1+K_2-(P_1+P_2)$,带入上面的结果对$L$求偏导数和导数,可得到力矩$\tau_1$和$\tau_2$的动力学方程$$\begin{align*}\tau_1=\frac{d}{dt}(\frac{\partial L}{\partial{\dot{\theta}}_1})-\frac{\partial L}{\partial \theta_1}\\ \tau_2=\frac{d}{dt}(\frac{\partial L}{\partial{\dot{\theta}}_2})-\frac{\partial L}{\partial \theta_2}\end{align*}$$
使用Mathematica进行符号计算得到的结果与牛顿欧拉法完全一致(两次计算的结果可以使用 Simplify 或 FullSimplify 对它们的差进行化简,然后判断结果是否为 0):
拉格朗日法计算力矩
(*拉格朗日法*)
K1 = 1/2 m1 (lc1 D[\[Theta]1[t], t])^2 + 1/2*1/12 m1 l1^2* D[\[Theta]1[t], t]^2;
P1 = m1 g lc1 Sin[\[Theta]1[t]];
\[Omega]1 = D[\[Theta]1[t], t];
\[Omega]2 = D[\[Theta]1[t], t] + D[\[Theta]2[t], t];
xc2 = l1 Cos[\[Theta]1[t]] + lc2 Cos[\[Theta]1[t] + \[Theta]2[t]];
yc2 = l1 Sin[\[Theta]1[t]] + lc2 Sin[\[Theta]1[t] + \[Theta]2[t]];
K2 = 1/2 m2 (D[xc2, t]^2 + D[yc2, t]^2) + 1/2*1/12 m2 l2^2*\[Omega]2^2;
P2 = m2 g yc2;
L = K1 + K2 - (P1 + P2);
f1 = D[D[L, Derivative[1][\[Theta]1][t]], t] - D[L, \[Theta]1[t]] // Simplify
f2 = D[D[L, Derivative[1][\[Theta]2][t]], t] - D[L, \[Theta]2[t]] // Simplify 
因此,不论用牛顿-欧拉方法还是用拉格朗日方法得到的动力学方程应该是相同的,差异仅在于建立封闭形式动力学方程的计算复杂性不同。牛顿-欧拉法只需考虑当前连杆和前一个连杆的关系,计算是局部的;而拉格朗日方程需要考虑整个系统的能量和相互作用,计算是全局的。牛顿-欧拉法的计算量通常远小于拉格朗日方程,主要因为它采用递推计算,避免了全局矩阵运算。对于多自由度机械臂的实时动力学仿真和控制,牛顿-欧拉法是更优的选择。而拉格朗日方程更适合理论分析和离线仿真,尽管计算量大,但其物理意义更加清晰。
参考:
刚体质量分布与牛顿-欧拉方程
二连杆机械臂阻抗控制模拟
使用JSXGraph模拟二连杆机械臂阻抗控制
《工业机器人技术基础》孙树栋 主编