P11592 [NordicOI 2024] Chair Game

先直接从 IMO2005 预选赛 C7 开始看。

---

问题：

给定一个长度为 \(n\) 的序列 \(a\)，保证 \(n\mid (\sum a_i)\)。证明存在两个排列 \(\sigma\) 与 \(\tau\)，使得 \(\sigma_i+\tau_i\equiv a_i\pmod n\)。

解：

若存在一个序列 \(a\) 和其的一组解 \((\sigma,\tau)\)，同时存在一个序列 \(b\)，与 \(a\) 有恰好两个位置值不同。考虑通过 \(a\) 和 \((\sigma,\tau)\) 得出 \(b\) 的一组解 \((\sigma',\tau')\)。如果能够完成这个问题，则证明了原问题。

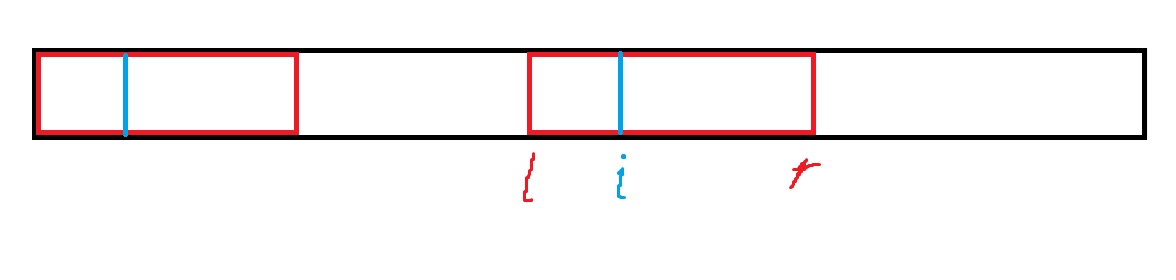
记两个序列不相同的位置为 \(i_1,i_2\)，对于 \(2\leq k < n\)，\(i_{k+1}\) 是唯一满足 \(\sigma_{i_{k-1}}+\tau_{i_{k+1}}\equiv b_{i_k}\) 的位置。

引理：记 \((p,q)\) 是最小的满足 \(i_p=i_q\) 的二元组，则一定有 \(p=1\) 或 \(p=2\) \(^\dagger\)。

于是我们得到了一组 \(b\) 的解 \((\sigma',\tau')\)：

\[\sigma'_{i_k}= \begin{cases} \sigma_{i_{q-1}} & k=1 \\ \sigma_{i_{k-1}} & 2\leq k<q \end{cases} \]

\[\tau'_{i_k}= \begin{cases} \tau_{i_1} & k=1\wedge p=2 \\ \tau_{i_2} & k=1\wedge p=1 \\ \tau_{i_{k+1}} & 2\leq k<q \end{cases} \]

\[\forall j\notin\{i_1\cdots i_{q-1}\},\sigma'_j=\sigma_j,\tau'_j=\tau_j \]

对于 \(j\neq i_1\)，\(\sigma'_j+\tau'_j\equiv b_j\) 都是根据定义得到的，而 \(\sum\sigma'_j+\sum\tau'_j=n(n+1)\equiv 0\equiv\sum b_j \pmod n\)，所以 \(\sigma'_{i_1}+\tau'_{i_1}\equiv b_{i_1}\) 自然成立。

\(\dagger\)：

对于引理的证明，假设 \(p>2\)，此时有：

\[\begin{aligned} \sum\limits_{k=p}^{q-1} b_{i_k} &=\sum\limits_{k=p}^{q-1} \sigma_{i_{k-1}}+\tau_{i_{k+1}}\\ &=\sigma_{i_{p-1}}+\sigma_{i_p}+\tau_{i_{q-1}}+\tau_{i_q}+\sum\limits_{k=p+1}^{q-2} \sigma_{i_k}+\tau_{i_k}\\ b_{i_p}+b_{i_{q-1}}&=\sigma_{i_{p-1}}+\sigma_{i_p}+\tau_{i_{q-1}}+\tau_{i_q} \end{aligned} \]

因为 \(i_p=i_q\)，所以上式变成 \(b_{i_{q-1}}=\sigma_{i_{p-1}}+\tau_{i_{q-1}}\)，也就是有 \(i_{p-1}=i_{q-1}\)，与 \((p,q)\) 定义相左，所以假设不成立。

翻译自：IMO Shortlist 2005

---

回到原问题，那么就相当于现在要使 \(\sigma_i+s_i\equiv \tau_i\pmod n\)，即 \(\tau_i-\sigma_i\equiv s_i\pmod n\)。

首先，\(n\mid(\sum s_i)\) 是有解的充要条件，充分性上面已经说过了。

必要性就是考虑最终答案序列 \(f_i\)，从 \(i\) 向 \((i+f_i)\bmod n\) 连边，最终一定要构成若干置换环，每个置换环内的 \(f_i\) 之和一定是 \(n\) 的倍数。所以 \(n\mid(\sum s_i)\) 是必要的。

于是就变成上面的问题了。

构造的话考虑先随便弄出一组合法的 \(a,(\sigma,\tau)\)，然后一位一位调整，直接模拟上述过程即可。时间复杂度 \(O(Tn^2)\)。

---

感觉 MO 的思路比较奇怪，有没有什么符合 OI 思维的思路，或者说上面那个东西实际上做的是什么？