Lifting The Exponent

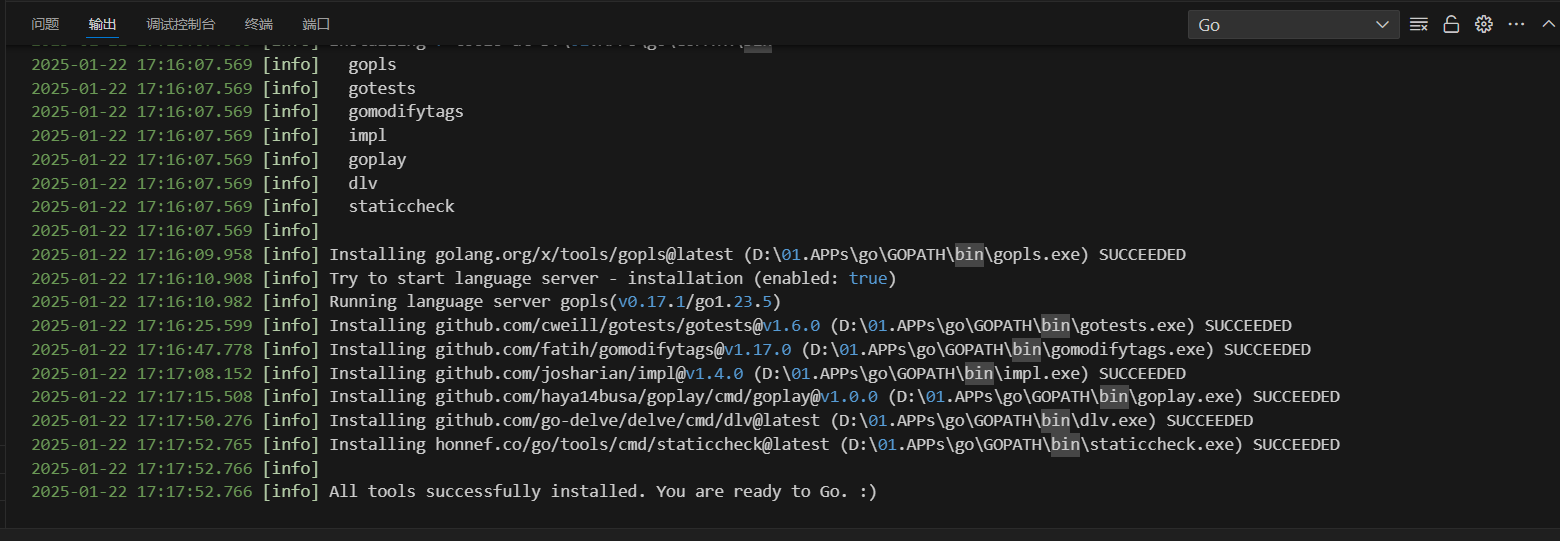
全文默认 \(p\) 为素数。

用 \(a,b\) 代表任意整数，用 \(x,y\) 代表不是 \(p\) 的倍数的整数。

Lemma 0

Part 1 直接的因式分解

\[\begin{aligned}& a^n - b^n \\=& (a-b) \sum\limits_{i=0}^{n-1} a^i b^{n-1-i} \end{aligned}\]

Part 2 凑 \(a-b\) 专用

\[\begin{aligned}& a^n - b^n \\=& ((a-b) + b)^n - b^n \\=& \sum\limits_{i=1}^n \binom n i (a-b)^i b^{n-i} \\=& (a-b) \sum\limits_{i=1}^{n} \binom n i (a-b)^{i-1} b^{n-i} \end{aligned}\]

通用的柿子

Lemma 1

若 \(p^k \mid (a-b)\)，则 \(p^{k+1} \mid (a^p - b^p)\)。

经典的特殊情况：若 \(p \mid (a-b)\)，则 \(p^2 \mid (a^p - b^p)\)。

Proof

由 Lemma 0，

\[\begin{aligned}& a^p - b^p \\=& (a-b) \sum\limits_{i=1}^p \binom p i (a-b)^{i-1} b^{p-i} \end{aligned}\]

每一项都是 \(p^{k+1}\) 的倍数。

Theorem 1

若 \(p \mid (a-b)\)：

\[\nu_p(a^n - b^n) \ge \nu_p(a - b) + \nu_p(n) \]

Proof

令 \(k = \nu_p(n)\)。

给 \(p^{\nu_p(a-b)} \mid a-b\) 套 \(k\) 层 Lemma 1 可知 \(p^{\nu_p(a-b) + k} \mid a^{p^k} - b^{p^k}\)。

由于 \(p^k \mid n\)，可知 \(a^{p^k} - b^{p^k} \mid a^n - b^n\)。（把 \(n\) 看成 \(p^k \times m\)，然后 \((a^{p^k})^m - (b^{p^k})^m\) 因式分解）

根据整除的传递性 \(p^{\nu_p(a-b) + k} \mid a^n - b^n\)，即 \(\nu_p(a^n - b^n) \ge \nu_p(a - b) + \nu_p(n)\)。

Example 1 经典老题

\(n\) 是正整数，\(a,b\) 是互不相等的整数，\(n \mid (a^n - b^n)\)。证明：\(n \mid \frac {a^n - b^n} {a - b}\)。

Proof

只要证 \(\forall p \mid n, \nu_p(\frac {a^n - b^n} {a-b}) \ge \nu_p(n)\)。

若 \(p \mid a - b\)，则由 Theorem 1 可知直接成立。

若 \(p \nmid a - b\)：\(\nu_p(\frac {a^n - b^n} {a-b}) = \nu_p(a^n - b^n)\)，再根据题目条件 \(\nu_p(a^n - b^n) \ge \nu_p(n)\)。

特殊条件下的等式

上面因为 \(a,b\) 自身可能是 \(p\) 的倍数，性质不好，得到的都是不等式。接下来我们换成 \(x,y\)，就能得到许多等式了。

（切记本文用 \(x,y\) 代表 \(p \nmid x, p \nmid y\)，没有这个条件时可能导致定理不成立）

Lemma 2

对于 \(p \nmid n\)，\(p \mid x-y\)，有

\[\nu_p(x^n - y^n) = \nu_p(x-y) \]

Proof

\[\begin{aligned}& x^n - y^n \\=& (x-y) \sum\limits_{i=0}^{n-1} x^i y^{n-i-1} \\=& (x-y) \sum\limits_{i=0}^{n-1} x^i (x+kp)^{n-i-1} \end{aligned}\]

求和算出来与 \(n \times x^{n-1}\) 在 \(\bmod p\) 下同余，因为 \(p \nmid n\) 且 \(p \nmid x\) 而不能为 \(0\)。

LTE

\(p\) 为奇素数，\(x,y\) 不是 \(p\) 的倍数，\(p \mid (x-y)\)。则对于任意正整数 \(n\)，有

\[\nu_p(x^n - y^n) = \nu_p(x - y) + \nu_p(n) \]

即

\[\nu_p\left(\frac {x^n - y^n} {x-y}\right) = \nu_p(n) \]

Proof

对于 \(p \nmid n\) 的情况已经在 Lemma 2 证过了。所以接下来只关心 \(p \mid n\)。

\[\begin{aligned}& \frac {x^n - y^n} {x-y} \\=& \sum\limits_{i=0}^{n-1} x^i y^{n-1-i} \\=& \sum\limits_{i=0}^{n-1} ((x-y) + y)^i y^{n-i-1} \\=& \sum\limits_{i=0}^{n-1} \sum\limits_{j=0}^i \binom i j (x-y)^j y^{n-j-1} \end{aligned}\]

考虑 Special Case: \(n=p\)。

\[\begin{aligned}& \frac {x^p - y^p} {x-y} \\=& \sum\limits_{i=0}^{p-1} \sum\limits_{j=0}^i \binom i j (x-y)^j y^{p-j-1} \end{aligned}\]

当 \(j \ge 2\) 时，\(\binom i j (x-y)^j y^{p-j-1}\) 必为 \(p^2\) 倍数，不管了。对于其余项：

\[\begin{aligned}& \sum\limits_{i=0}^{p-1} y^{p-1} + i (x-y) y^{p-2} \\=& p \times y^{p-1} + \frac {p (p-1)} 2 (x-y) y^{p-2} \\\equiv& p \times y^{p-1} \pmod {p^2} \end{aligned}\]

（在这个地方用到了 \(p\) 是奇数的性质，导致了以后 \(p=2\) 需要单独讨论）

这意味着 \(\nu_p\left(\frac {x^n - y^n} {x-y}\right) = 1\)。Special Case 证毕。

对于剩余情况，令 \(n = p^a \times b\)，其中 \(p \nmid b\)。

\[\begin{aligned}& \nu_p(x^n - y^n) \\=& \nu_p((x^{p^a})^b - (y^{p^a})^b) \\=& \nu_p(x^{p^a} - y^{p^a}) & \text{Lemma 2} \\=& \nu_p((x^{p^{a-1}})^p - (y^{p^{a-1}})^p) \\=& \nu_p(x^{p^{a-1}} - y^{p^{a-1}}) + 1 & \text{Special Case} \\=& \nu_p(x-y) + a & \text{Mathematical induction} \end{aligned}\]

证毕。