训练情况

A题
前缀和模板题,我们输入完 \(a_i\) 后直接求前缀和 \(a_i = a_i + a_{i-1}\),求区间 \([l,r]\) 的和就为 \(a_r-a_{l-1}\)
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,m;cin>>n>>m;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 2;i<=n;i++) a[i] += a[i-1];while(m--){int l,r; cin>>l>>r;cout<<a[r] - a[l-1]<<endl;}
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
B题
差分模板题,我们记 \(p_i = a_i - a_{i-1}\),区间加只需要在 \(p_l += k,p_{r+1} -= k\),最后再求一遍前缀和即可
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,m; cin>>n>>m;vector<int> a(n + 1),p(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 1;i<=n;i++) p[i] = a[i] - a[i-1];while(m--){int l,r,k; cin>>l>>r>>k;p[l]+=k;p[r+1]-=k;} for(int i = 1;i<=n;i++) p[i] += p[i-1];for(int i = 1;i<=n;i++) cout<<p[i]<<" ";
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
C题
\(n\) 个数里头尾删掉 \(k\) 个数,可以等价为连续选 \(n-k\) 个连续的数求和,区间求和问题我们可以使用前缀和预处理
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,k; cin>>n>>k;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 1;i<=n;i++) a[i] += a[i-1];int ans = 0;for(int i = 1;i+n-k-1<=n;i++) ans = max(ans,a[i+n-k-1] - a[i-1]);cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
D题
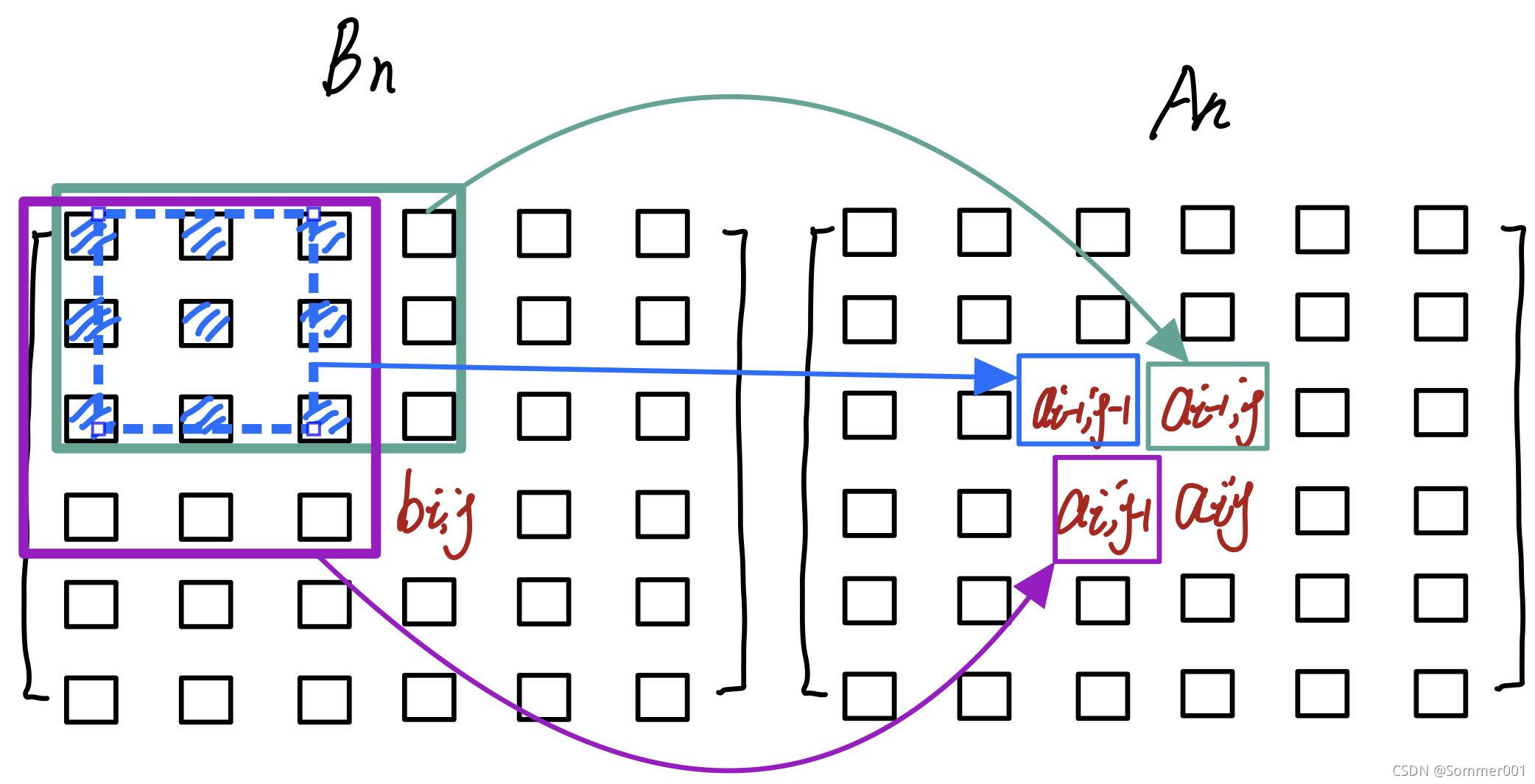
二维差分再前缀和,输入矩阵的左上角 \((xa,ya)\) 右下角 \((xb,yb)\),其中我们差分数组 \((xa,ya)\) 加一,即从 \((xa,ya)\) 到 \((n,n)\) 的地毯数全部加一,所以我们差分数组 \((xb+1,yb+1)\) 减一,即从 \((xb+1,yb+1)\) 到 \((n,n)\) 的地毯数全部减一,剩下了两个区域 \((xb+1,ya),(xa,yb+1)\) 再减一,最后再求一遍二维前缀和查询即可
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n,m; cin>>n>>m;vector<vector<int>> a(n + 2,vector<int>(n + 2));while(m--){int xa,ya,xb,yb; cin>>xa>>ya>>xb>>yb;++a[xa][ya];++a[xb+1][yb+1];--a[xb+1][ya];--a[xa][yb+1];}for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){a[i][j] += a[i][j-1];}}for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){a[i][j] += a[i-1][j];}}for(int i = 1;i<=n;i++){for(int j = 1;j<=n;j++){cout<<a[i][j]<<" ";}cout<<endl;}
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
E题
选取当前卡牌到最左边实际上就是区间 \([1,r]\) 求和,直接前缀和处理,想要答案最大,前缀和贡献只能为正,至少选择两张,所以要从二开始
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 1;i<=n;i++) a[i] += a[i-1];int ans = 0;for(int i = 2;i<=n;i++) if(a[i] > 0) ans += a[i];cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
F题

等差数列差分一次还是有公差 d 的存在,所以我们再差分一次就可以做到 \(O(1)\) 更新了,差分后的结果如上图,最后跑两边前缀和就是答案
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,m; cin>>n>>m;vector<int> a(n + 5);while(m--){int l,r,s,e; cin>>l>>r>>s>>e;int res = (e - s) / (r - l);a[l] += s;a[l+1]+=(res-s);a[r+1] -= (res + e);a[r+2] += e;}for(int i = 1;i<=n;i++) a[i] += a[i-1];for(int i = 1;i<=n;i++) a[i] += a[i-1];int ans = 0,ma = 0;;for(int i = 1;i<=n;i++) ans ^= a[i],ma = max(ma,a[i]);cout<<ans<<" "<<ma<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
G题
直接枚举区间 \([l,r]\) 的时间复杂度为 \(O(n^2)\) 会超时,对于区间求和的问题我们容易想到前缀和,但是我们需要处理区间是 \(k\) 的倍数,我们考虑对前缀和对 \(k\) 取模(取余数),如果位置 \(l,r\) 的前缀和 \((p_l \mod k) = (p_r \mod k)\) 则说明区间 \([l,r]\) 的和一定是 \(k\) 的倍数,因为 \((x \mod b) = ((x + kb) \mod b)\),所以我们需要统计 \(p_i\) 余数的出现次数,遍历的时候查询当前位置余数在前面出现了几次,就是有几个区间,答案加上区间个数即可,注意一下初始条件,详情见代码
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,k; cin>>n>>k;int a[n+1],pre[n+1],cnt[n+1];pre[0] = 0;for(int i = 1;i<=n;i++) cin>>a[i],cnt[i] = 0;for(int i = 1;i<=n;i++) pre[i] = pre[i-1] + a[i];for(int i = 1;i<=n;i++) pre[i] %= k;cnt[0] = 1;int ans = 0;for(int i = 1;i<=n;i++){ans += cnt[pre[i]];cnt[pre[i]]++;}cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
H题
https://www.luogu.com.cn/article/0kz22o0v