二分查找
思路
运用二分查找,逐渐逼近所要查找的数字
代码
#include<iostream>
using namespace std;
int binary_search(int arr[],int l,int r,int x){int mid;while(l<r){mid=(l+r)>>1;if(arr[mid]>=x) r=mid;else l=mid+1;}return arr[l];
};
int main(){int n;cin>>n;int arr[n];for(int i=0;i<n;++i){cin>>arr[i];}int q=0;cin>>q;for(int i=0;i<q;++i){int x;cin>>x;int xx=binary_search(arr,0,n,x);if(xx==x) cout<<"Yes"<<endl;else cout<<"No"<<endl;}return 0;
}
A-B数对
思路
差值是常数c,那么确定A,B中的一个数就可以确定另一个,然后查找数组中有几个这样的数字就可以确定有几组以“B”为被减数的数对
题目给出一串正整数,但不一定是有序的正整数,如果是有序的正整数就可以按B递增或递减的顺序依次来计算以“B”为被减数有几组数对。
首先先对这串数字排序,这里为从小到大的顺序。然后用二分查找的方法找到最左边的符合条件的“A”因为可能符合条件的“A”的个数不止一个,然后向右遍历得到"A"的个数进行计数。并将这组"A","B"数对的个数加入总计数器中。
进阶,找到最左边后再用二分法找到最右边“A”,用这两个得坐标进行计算就可以在O(1)的时间复杂度里面得结果。
本题值得注意的是计数的取值范围,N的数量级是10的5次方,数对的个数很可能是N^2的数量级,所以计数器要记得用long long类型。
代码
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll binary_search(vector<int>&arr,int l,int r,int x){int mid;ll cnt=0;while(l<r){//找到最左边大于等于x的值 mid=(l+r)>>1;if(arr[mid]>=x) r=mid;else l=mid+1;} while(arr[l++]==x) ++cnt;return cnt;
}
int main(){int n,c;ll cnt_n=0,tem_cnt=0;cin>>n>>c;vector<int> arr(n);for(int i=0;i<n;++i){cin>>arr[i];}sort(arr.begin(),arr.end());// for(int i=0;i<n;++i){if(i>0&&arr[i]==arr[i-1]){cnt_n+=tem_cnt;continue;}tem_cnt=binary_search(arr,i+1,n,arr[i]+c);cnt_n+=tem_cnt;}cout<<cnt_n;return 0;
}
#include<bits/stdc++.h>
using namespace std;
#define MAX 200001
int N,C,lis[MAX];
long long cnt_ans=0;
int low_bound(int l,int r,int A){//找A左边界 int mid;while(l<r){mid=l+r>>1;if(lis[mid]>=A) r=mid;//因为l+r>>1是向下取整,最终会落在l但是由于边界控制是r,所以最终不会死循环。 else l=mid+1; }return l;
}
int up_bound(int l,int r,int A){//找A的右边界 int mid;while(l<r){mid=l+r+1>>1;if(lis[mid]<=A) l=mid;//如果向下取整就会死循环。 else r=mid-1;}return l;
}
int main(){cin>>N>>C;for(int i=0;i<N;++i) cin>>lis[i];sort(lis,lis+N);for(int i=0;i<N-1;++i){int r=up_bound(i+1,N-1,lis[i]+C);int l=low_bound(i+1,N-1,lis[i]+C);if(lis[l]==lis[r]&&lis[l]==lis[i]+C) cnt_ans+=(r-l+1);}cout<<cnt_ans;return 0;
}
分巧克力
思路
有N块巧克力,分给K个人,每个人获得的巧克力为边长为a的正方形巧克力。所以巧克力至少分的k块巧克力,大于等于k的值都是答案区间,但本题希望得到的巧克力尽可能的大,也就是块数尽可能的少。本题是二分答案求最大值里的最小值问题。
左边界是1,有边界是巧克力的可能取值的最大边长。
check函数的关键是要检查长度为mid的巧克力是否能够分出至少k块正方形巧克力。如果分得得块数多于k块,就需要将巧克力得边长的答案范围拉长,让左边界变大,如过分的的块数连k块都不足,就需要将有边界拉到mid-1处,使得有边界变小。
注意:
-
有边界不可以是INT_MAX,因为这个值随便加一个正数就会溢出,答案是错误的,但是比题目中的最大取值大的都是可以的
-
不一定所有的巧克力都会被分割,也就是不需要保证有边界的大小小于巧克力所有边长的最小值。题目只要求能够分够k块就好了,即使有的巧克力没有被分到,也可能使得块数足够且每个人分得的巧克力的边长的大小更大
代码
#include<iostream>
#include<climits>
using namespace std;
bool check(int choc[][2],int N,int K,int x){int cnt_n=0;for(int i=0;i<N;++i){cnt_n+=(choc[i][0]/x)*(choc[i][1]/x);if(cnt_n>=K) return true;}return false;
}
int binary_search(int choc[][2],int l,int r,int N,int K){int mid;while(l<r){mid=(l+r+1)>>1;//这样就会尽可能的去尝试大的一个 if(check(choc,N,K,mid)) l=mid;else r=mid-1;}return l;
}
int main(){int N,K,l=1,r=100001; //如果有边界是INT_MAX,一加值就会爆掉,所以不能用INT_MAXcin>>N>>K;int choc[N][2];//用来存储N块巧克力的H和Wfor(int i=0;i<N;++i){cin>>choc[i][0]>>choc[i][1];//不一定保证所有巧克力都被分割,所以不需要记录所有边长的最小值}cout<<binary_search(choc,1,r,N,K);return 0;
}
卡牌
思路
方案一
实际操作时,我会先将这些卡牌根据已经有张数ai为第一关键字和可以画的张数bi为第二关键字进行排序,然后根据短板原则,补短板,先看最短的板和倒数第二短差多少,然后先看第二关键字bi最小的那个是否可以被补上,不行就直接结束,可以的话就看剩下的空白卡篇是否可以将每一种卡牌都补上,如果手中的卡牌只能补上一部分甚至一种都补不上就直接结束。
但是我认为这种方案的代码实现非常的困难,以及考虑的情况很多。还有数据类型的问题,所以最终放弃了这种方案另寻他法。本来想的是补差值那个diff的地方用二分答案,看看最多可以使所有短板补多少可以补上。
方案二
在借鉴了一番似乎找到了二分答案的精髓,”答案“。本题的答案是最终可以补全卡牌的数量,所以我只需要确定最少可以有几副卡牌,最多可以有几副卡牌,然后在答案区间判断究竟哪个数值可以满足题意而且还是最大的。所以是找最小值里的最大值
左边界就是现在已经有的卡牌里的张数最小的 ai ,右边界是假设 i 种卡牌已经有的 ai 加上可以补上的卡牌 bi 的 ai+bi 的最大值。
check函数是要看如果我要分mid副牌,我拥有的m张空牌和每种牌可以被添加的个数是否都能够满足要求
循环遍历所有种类的卡牌。如果当前卡牌的比mid小且距离mid的差值大于这种卡牌可以被添加的卡牌的数量,那么说明mid的值偏大,返回false,如果可以被补上就从m里扣除,如果m扣除不了,就说明mid偏大就要返回false,如果可以则继续。如果当前种类的卡牌的个数比mid还大,那就不需要从m中扣除,m-0即可,循环进入下一种类的判断。
代码
#include<iostream>
#include<climits>
using namespace std;
bool check(int mid,int a[],int b[],int n,long long m){long long cnt=0;for(int i=0;i<n;++i){if(max(mid-a[i],0)<=b[i]){cnt+=std::max(mid-a[i],0);}else return false;}if(cnt>m) return false;return true;
}
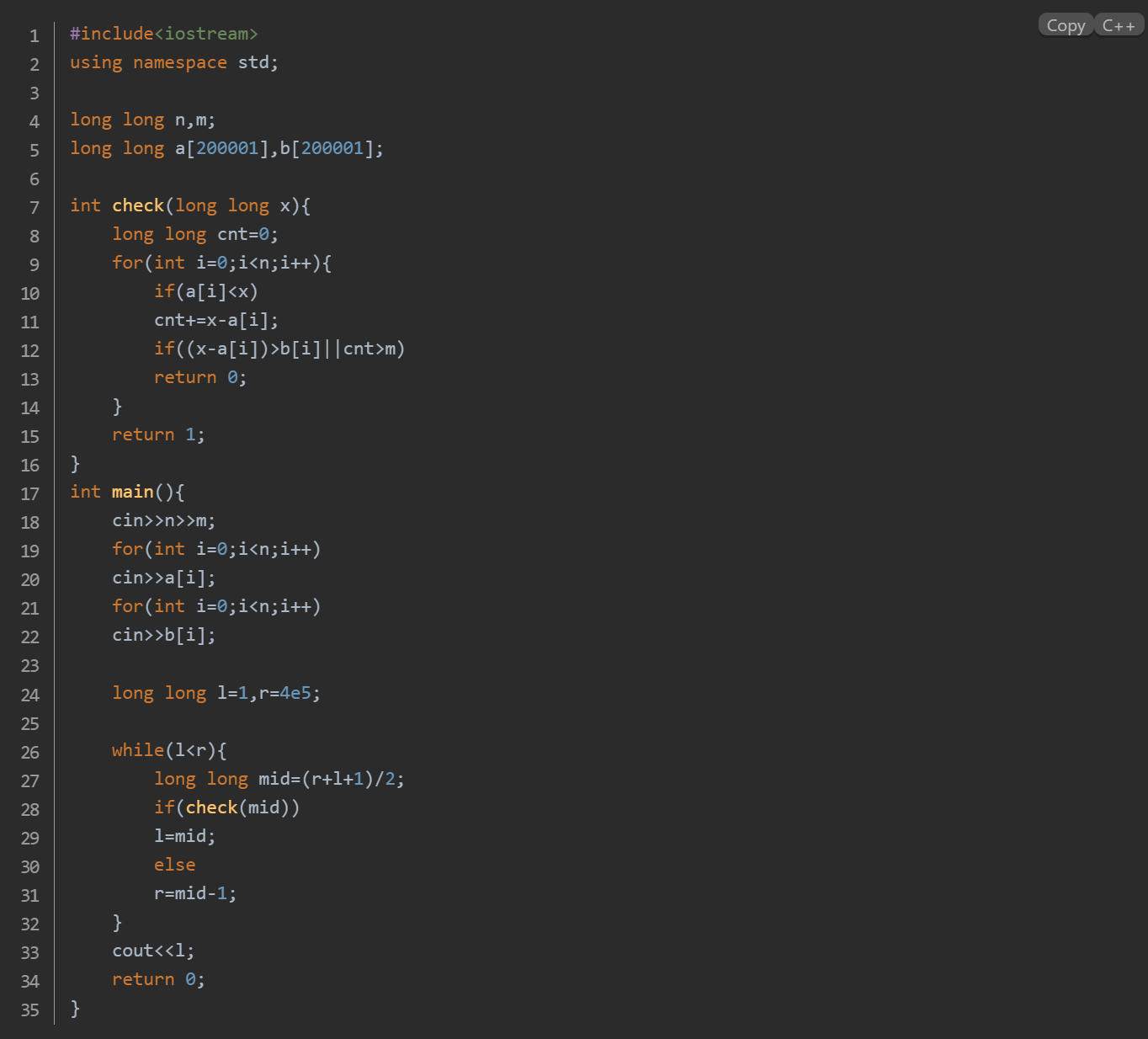
int main(){//数据输入 int n,l=INT_MAX,r=INT_MIN;long long m;cin>>n>>m;int a[n],b[n];for(int i=0;i<n;++i){cin>>a[i];l=min(a[i],l);}for(int i=0;i<n;++i){cin>>b[i];r=max(r,a[i]+b[i]);} int mid;while(l<r){mid=l+r+1>>1;if(check(mid,a,b,n,m)) l=mid; else r=mid-1;} cout<<l;return 0;
}
书的复制
思路
如果要时间尽可能的少,那肯定平均分页数花的时间最短,但是本题加了限制,每个人抄书的页数必须是完整的并且抄书的编号一定是连续的。但是这几个人的抄书的速度是一样的,所以需要保证的这几个人所抄写的书的页数最多的那个人在所有分法里面的最小即可,即本题是求最大值里的最小值 还是二分答案
答案是什么,每个人分的书的编号范围,其实也可以映射到书的页数上。抄写的最少是页数最少的那本书,最多是一个人抄写所有页数的书。这样答案区间就划分出来了
check函数就是检查每个人最多抄写mid页时,可以怎样分配,要看每个人最多抄写mid页时需要几个人来抄写。当抄写的人数大于k时,说明mid偏小了,需要让左边界为mid+1,当抄写的人数小于等于k时,说明mid是大于等于答案的,也就是在答案区间,需要让右边界等于mid,最终需要找到使得最大值边界可以使得分成k组,并且这个最大值是所有满足条件里面的最小的。
题目还要求尽可能让后面的写,前面的不写。所以我们得到最小的最大值后就倒着分配,先从书编号大的分配给后面的人,这样自然前面的人剩下的书就会相对较少。尽可能的让后面的人去贴近最大值。
注意:页数题目中没给数的取值范围,有可能需要long long 类型
代码
#include<iostream>
#include<climits>
using namespace std;
int m,k;
long long page[501],maxn=LLONG_MIN,sum=0;
bool check(int x){long long sum=0,cnt=1;for(int i=0;i<m;++i){if(sum+page[i]<=x) sum+=page[i];else{cnt++;sum=page[i];}}if(cnt<=k) return true;else return false;
}
int main(){cin>>m>>k;for(int i=0;i<m;++i){cin>>page[i];maxn=max(maxn,page[i]);sum+=page[i];}long long l=maxn,r=sum;int mid;while(l<r){mid=l+r>>1;if(check(mid)) r=mid;else l=mid+1;}int bro=l,it[501],cnt=1;it[0]=m;long long s=0;for(int i=m-1;i>=0;--i){if(s+page[i]<=bro) s+=page[i];else s=page[i],it[cnt++]=i+1;}it[cnt]=0;for(int i=cnt;i>0;--i){cout<<it[i]+1<<" "<<it[i-1]<<endl;}return 0;
}
青蛙过河
思路
本题很容易想到二分答案是青蛙的跳跃能力,左边界是1,右边界是河岸的最大长度
但问题是check函数如何撰写,怎样才能判断跳跃能力为y的青蛙能不能过河2*x次,难道要动态规划,难道要递归?
要不说计算机算法的进步还得靠数学。青蛙跳过去又跳回来其实完全等效于两只青蛙都从河的左边跳到右边,只是跳的方案不一样罢了。
一只青蛙跳2 * x次,也可以等效为2 * x只青蛙跳一次过河。好像说了句屁话,但实际上只是想说明2 * x次跳跃的方向是不变的,都是从河的左边跳到河的右边。
现在来想,如果2 * x只青蛙只跳一次会落到[1,y]这个区间上,而且每一只青蛙都会落在这个区间上,说明什么?说明这个区间上的石墩子的H值加起来至少得是2 * x才能承受2 * x次的跳跃。但是只有这一段似乎说明不了什么问题,但其实是在河水中的每一段长度为y的区间,石墩子的H值加起来都得大于等于2 * x才可以。为什么?
我们任取一段河流中长度为y的线段。有三类青蛙,分别是还没进这段线段的,在这个线段上的,已经从这段跳走的,我敢说,所有青蛙肯定都至少在这段跳过一次。
还没进来的最长跳y,他跳最远也肯定会落尽这个区域。你说他只跳一步?ok,只跳一步确实可能没有落在这个区段,但是他会落在离他最近的那个区段,然后继续跳,最坏情况,这只青蛙也会从我开始举例的这段的前一段跳到这一段。
本来就在这个区段的青蛙好说,他已经在了
已经跳过的青蛙呢?离得近的肯定就可以从这跳出去,离得远的也是从这段跳出去后又跳走的。
要想青蛙能顺利过河,每段长度为y的区间内的H和必定大于等于x。但是这就够了?这只是必要性,但还需要证明充分性。
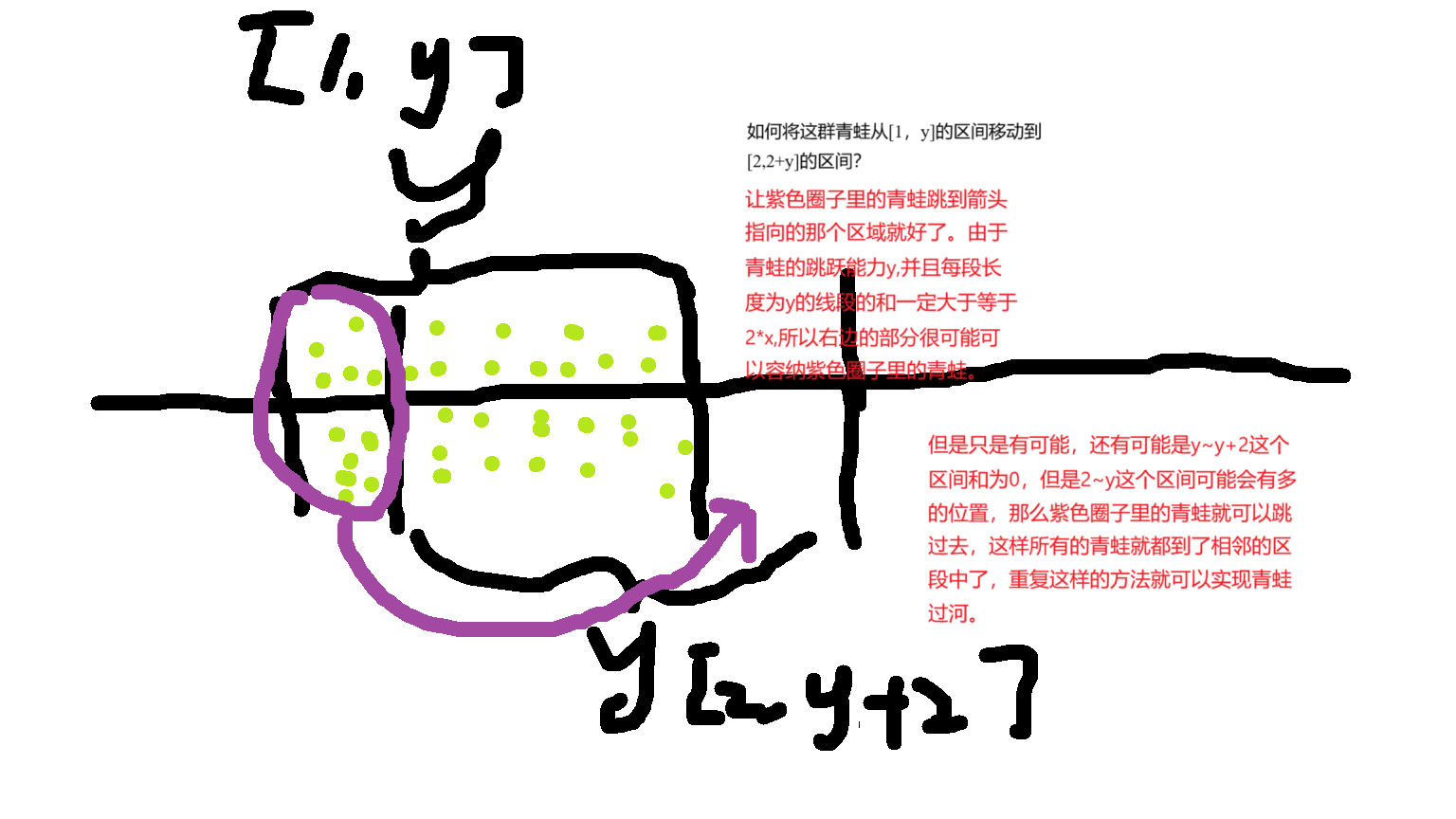
我通过上面一张图来证明每段和为2 * x就可以使得2 * x只青蛙过河,也就是一只青蛙往返共计2 * x次。
代码
#include<iostream>
using namespace std;
int n,x,l,r;//要度过2*x次这条河
int i,j;
int st[100001],sum[100001];
bool check(int mid){for(int i=1;i+mid<=n;++i){if(sum[i+mid-1]-sum[i-1]<2*x) return false;}return true;
}
int main(){cin>>n>>x;l=1,r=100001;for(i=1;i<n;++i){cin>>st[i];sum[i]=sum[i-1]+st[i];}int mid;while(l<r){mid=l+r>>1;if(check(mid)) r=mid;else l=mid+1;}cout<<l;return 0;
}
学习总结
//这里面的l,r是闭区间[l,r];
#define MAX 200001;
obj lis[MAX];
int low_bound(int l,int r,obj x){//找大于等于x的最小值int mid;while(l<r){mid=l+r>>1;if(lis[mid]>=x) r=mid;else l=mid+1;}return l;
}
int up_bound(int l,int r,obj x){//找小于等于x的值的最大值int mid;while(l<r){mid=l+r+1>>1;//这里是向上取整,防止掉入死循环。if(lis[mid]<=x) l=mid;else r=mid-1;}return l;
}
二分答案
二分答案的常见套路就是找到本题答案所在的取值范围,然后二分答案遍历这个范围,根据check函数找到符合条件的值
二分答案的不同之处在于check函数放在循环里的if语句上
//这里面的l,r是闭区间[l,r];
#define MAX 200001;
obj lis[MAX];
int low_bound(int l,int r){//找大于等于x的最小值int mid;while(l<r){mid=l+r>>1;if(check(mid)) r=mid;else l=mid+1;}return l;
}
int up_bound(int l,int r){//找小于等于x的值的最大值int mid;while(l<r){mid=l+r+1>>1;//这里是向上取整,防止掉入死循环。if(check(mid)) l=mid;else r=mid-1;}return l;
}
本次练习
“分巧克力”需要在check里判断边长为mid的巧克力被分割的个数于人数k的关系。
“卡牌” 需要判断要分成mid副卡牌,现有的控纸牌和每种卡牌手写上限是否能够满足
“书的复制”则需要检查mid为上限需要的人数是否可以被满足
“青蛙过河”则是需要判断跳跃能力为mid是否可以使得青蛙在这条河上跳跃经过这条河2 * x次。