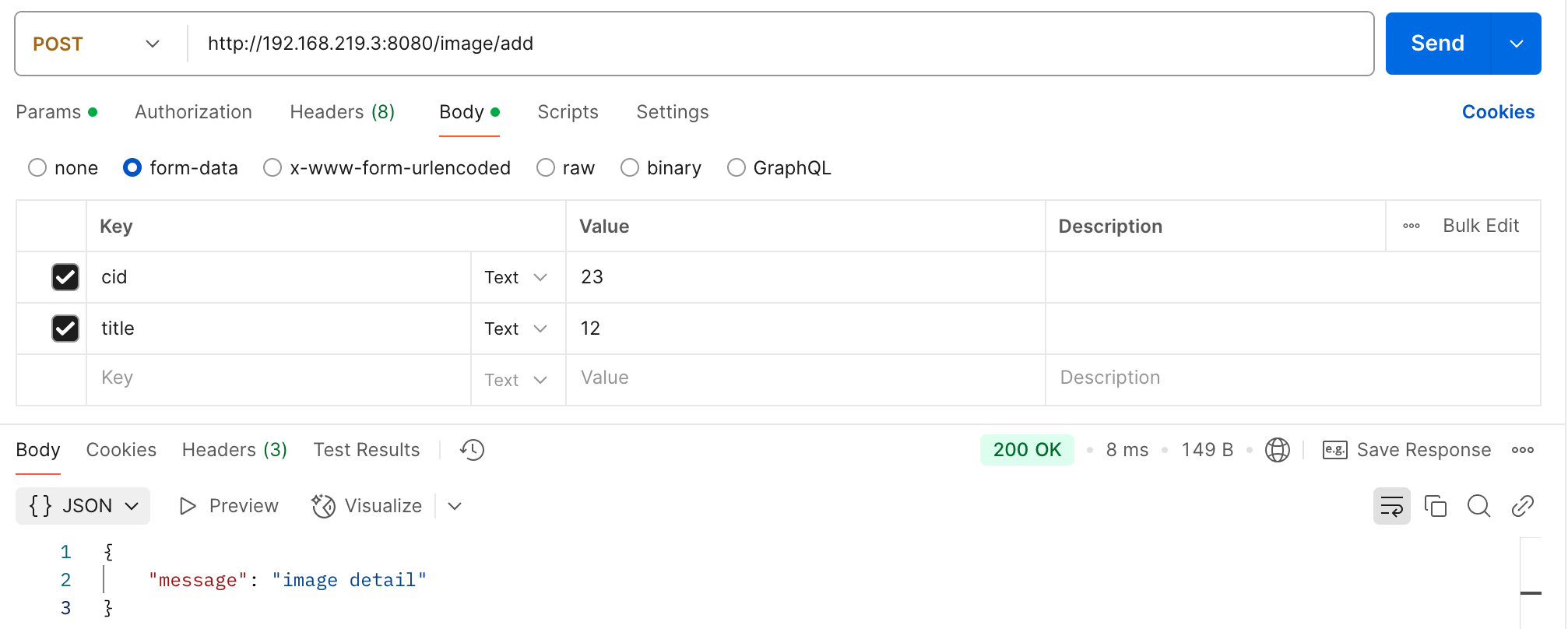
\[\text{P1.} \int\tan(x)\sqrt{2+\sqrt{4+\cos(x)}}\text{dx}
\]
考虑到 \(sin\) 是 \(cos\) 的微分,把 \(tan\) 上面放到微分里。于是可做换元 \(t=\sqrt{2+\sqrt{4+\cos(x)}}\) ,得到 \(\cos(x)=t^4-4t^2\) ,所以原式可变为 \(-4\displaystyle\int\dfrac{t(t^3-2t)}{t^4-4t^2}\text{dt}\) ,这就很简单了,是 \(-4\left(t+\dfrac{1}{2}\ln\left(\dfrac{t-2}{t+2}\right)\right)+C\) ,回代得到:
\[\text{A1.}-4\sqrt{2+\sqrt{4+\cos(x)}}-2\ln\left(\dfrac{\sqrt{2+\sqrt{4+\cos(x)}}-2}{\sqrt{2+\sqrt{4+\cos(x)}}+2}\right)+C
\]
\[\text{P2.} \int_0^{\infty}\dfrac{\text{dx}}{\left(x+1+\lfloor2\sqrt{x}\rfloor\right)^2}
\]
先经典的换元 \(t=2\sqrt{x}\) ,于是原式变为
\[\displaystyle\int_0^\infty\dfrac{\frac{1}{2}t\text{dt}}{\left(\frac{1}{4}t^2+1+\lfloor t\rfloor\right)^2}
\]
整理一下系数然后分段得到
\[\displaystyle 4\sum\limits_{n=0}^\infty\int_n^{n+1}\dfrac{2t\text{dt}}{\left(t^2+4(1+n)\right)^2}=4\sum\limits_{n=0}^\infty\dfrac{1}{(n+2)^2}-\dfrac{1}{4(n+1)(n+5)}
\]
前面是平方倒数和,后者裂项。
\[\text{A2.} \dfrac{2\pi^2}{3}-\dfrac{73}{12}
\]
\[\text{P3.}\int_0^{10}\left\lfloor\left(\dfrac{1+\sqrt{5}}{2}\right)^{\lfloor x\rfloor}\right\rfloor\text{dx}
\]
显然分段为 \(\displaystyle\sum\limits_0^9\int_n^{n+1}\left\lfloor\left(\dfrac{1+\sqrt{5}}{2}\right)^n\right\rfloor\text{dx}\) ,注意到这个是斐波那契数列的一个 \(\rho\) ,所以我们可以考虑构造一个特殊的斐波那契数列,满足
\[f_n=\left(\dfrac{1+\sqrt{5}}{2}\right)^n+\left(\dfrac{1-\sqrt{5}}{2}\right)^n
\]
这个的递推数列是满足斐波那契的,但初值不同: \(f_0=2,f_1=1\)
那么原题即求 \(\displaystyle\sum\limits_0^9\left\lfloor f_n-\left(\dfrac{1-\sqrt{5}}{2}\right)^n\right\rfloor\)
考虑其正负性的误差后,答案即为 \(S_9-5\)
\[\text{A3.} 193
\]
\[\text{P4.}\int_0^{\pi}\max(|2\sin(x)|,(2\cos(2x)-1))^2\cdot\min(|\sin(2x)|,|\cos(3x)|)^2\text{dx}
\]
观察发现 \(\sin(2x)=2\sin(x)\cdot\cos(x),\cos(3x)=(2\cos(2x)-1)\cdot\cos(x)\)
于是我们设 \(f(x)=2\sin(x),g(x)=2\cos(2x)-1\)
所以所求即为
\[\begin{aligned}&\int_0^{\pi}(\max(f(x),g(x))\min(f(x),g(x))\cdot\cos(x))^2\text{dx}\\=&\int_0^{\pi}(\sin(2x)(2\cos(2x)-1))^2\text{dx}\\=&\int_0^{\pi}(\sin(4x)-\sin(2x))^2\text{dx}\end{aligned}
\]
换元,然后利用三角函数正交性可以得到答案。
\[\text{A4.}\pi
\]
\[\text{P5.}\int_0^1\left(\sqrt{\dfrac{1}{4x^2}+\dfrac{1}{x}-x}-\sqrt{\dfrac{x^4}{4}-x+1}-\dfrac{1}{2x}\right)\text{dx}
\]
考虑换元后相消。观察到第一项和第三项分母相同,考虑把这两项换元。
\[y=\sqrt{\dfrac{1}{4x^2}+\dfrac{1}{x}-x}-\dfrac{1}{2x}=\dfrac{-1+\sqrt{1-4x(x^2-1)}}{2x}
\]
类似二次函数求根公式,写出来得到 \(x\cdot y^2+y+(x^2-1)=0\)
那么可以反过来写出 \(x=\dfrac{-y^2}{2}+\sqrt{\dfrac{y^4}{4}-y+1}\)
发现这跟题目中的第二项结构相同,于是
\[\begin{aligned}&\int_0^1\left(\sqrt{\dfrac{1}{4x^2}+\dfrac{1}{x}-x}-\dfrac{1}{2x}\right)\text{dx}\\=&\int_0^1y\text{dx}\\=&xy\bigg|_0^1-\int_1^0x\text{dy}\\=&\int_0^1\left(\dfrac{-y^2}{2}+\sqrt{\dfrac{y^4}{4}-y+1}\right)\text{dy}\end{aligned}
\]
把 \(y\) 看成 \(x\) 得到
\[\int_0^1\left(\sqrt{\dfrac{1}{4x^2}+\dfrac{1}{x}-x}-\sqrt{\dfrac{x^4}{4}-x+1}-\dfrac{1}{2x}\right)\text{dx}=\int_0^1\dfrac{-y^2}{2}\text{dy}
\]
\[\text{A5.}-\dfrac{1}{6}
\]
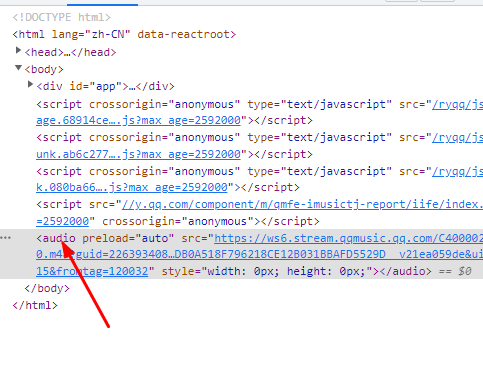

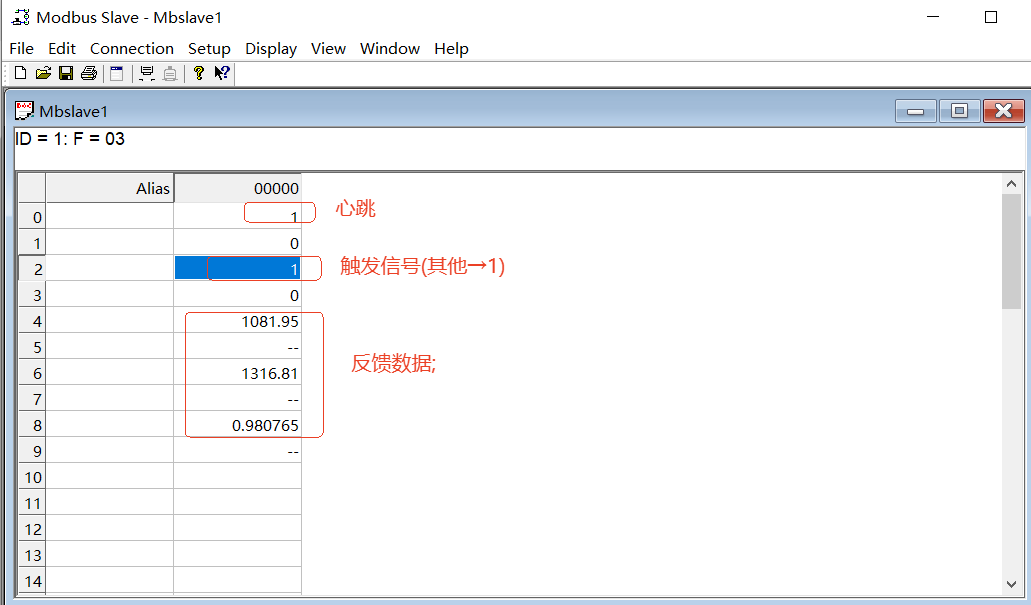
![[SWPUCTF 2021 新生赛]easyupload3.0 Writeup](https://img2024.cnblogs.com/blog/3596444/202501/3596444-20250131161820412-287649955.png)