搜索play的第三弹!
回家
题目描述
小 H 在一个划分成了 \(n \times m\) 个方格的长方形封锁线上。 每次他能向上下左右四个方向移动一格(当然小 H 不可以静止不动), 但不能离开封锁线,否则就被打死了。 刚开始时他有满血 \(6\) 点,每移动一格他要消耗 \(1\) 点血量。一旦小 H 的血量降到 \(0\), 他将死去。 他可以沿路通过拾取鼠标(什么鬼。。。)来补满血量。只要他走到有鼠标的格子,他不需要任何时间即可拾取。格子上的鼠标可以瞬间补满,所以每次经过这个格子都有鼠标。就算到了某个有鼠标的格子才死去, 他也不能通过拾取鼠标补满 HP。 即使在家门口死去, 他也不能算完成任务回到家中。
地图上有五种格子:
0:障碍物。
1:空地, 小 H 可以自由行走。
2:小 H 出发点, 也是一片空地。
3:小 H 的家。
4:有鼠标在上面的空地。
小 H 能否安全回家?如果能, 最短需要多长时间呢?
输入格式
第一行两个整数 \(n,m\), 表示地图的大小为 \(n \times m\)。
下面 \(n\) 行, 每行 \(m\) 个数字来描述地图。
输出格式
一行, 若小 H 不能回家, 输出 -1,否则输出他回家所需最短时间。
样例 #1
样例输入 #1
3 3
2 1 1
1 1 0
1 1 3
样例输出 #1
4
提示
对于所有数据,\(1 \le n,m \le 9\)。
2021.9.2 增添一组 hack 数据 by @囧仙
解法&个人感想
这题不可能是橙题啊喂!我调的都想不做了!
而且题解还打不开!
列举一下这题的坑点吧
首先:卡DFS DFS的point 1必定TLE
然后:因为可能反复经过某个鼠标格子从而回满血,所以vis不止是0和1
那应该是什么呢?想了很久发现 因为vis和step是独立的 vis只针对能不能到这回事
然后ans只要到了才更新(所以得先满足到了吧!)
因此 vis应该记录到当前格子的最大生命(如果小于就回溯 不然怎么到得了嘛)
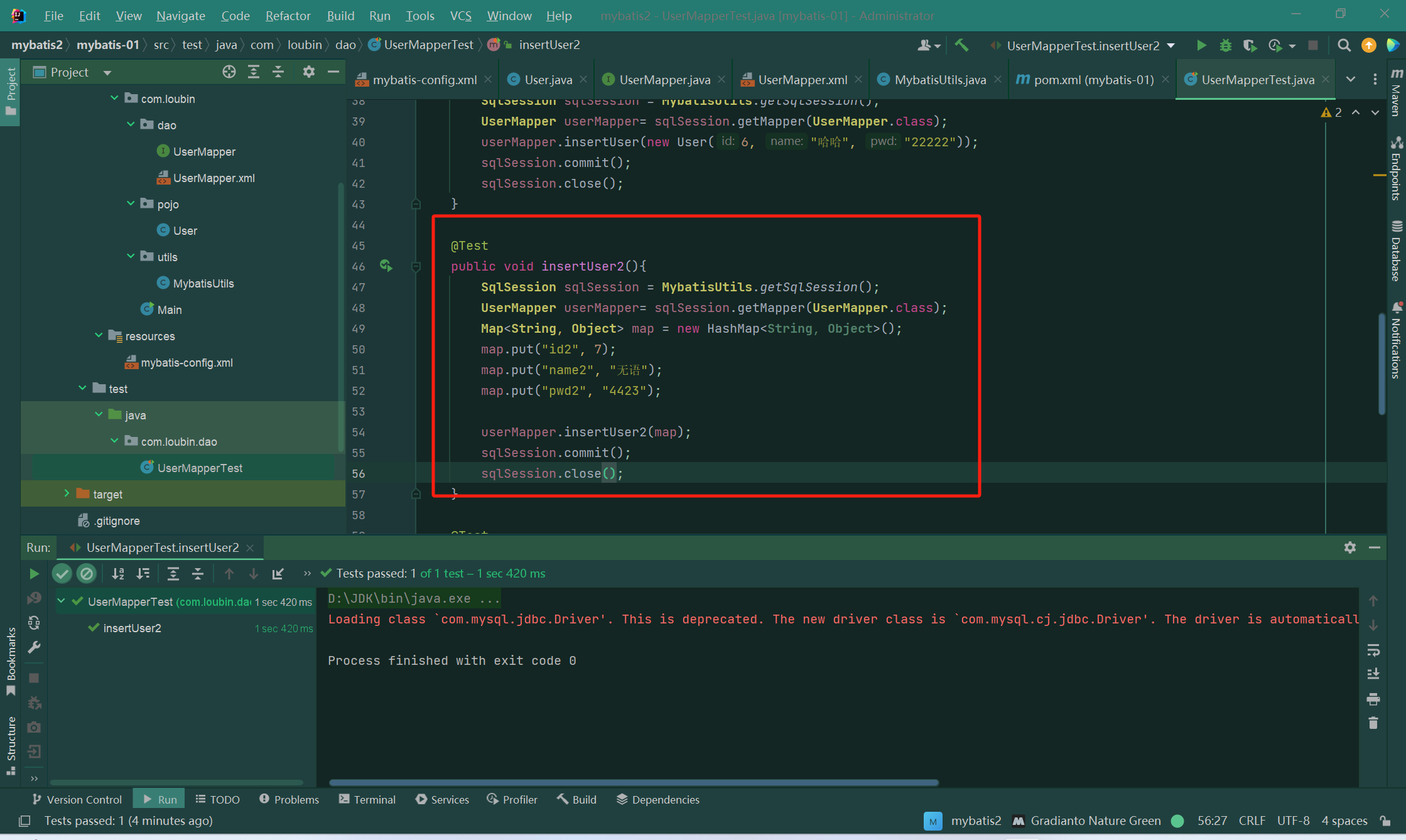
下面看代码吧!
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m;
int ma[11][11];
int vis[11][11];
int dx[5]={0,0,0,1,-1},dy[5]={0,1,-1,0,0};
int sx,sy,fx,fy;
const int INF=1e9;
int ans=INF;//ans赋大值来看它是否变化
struct node{int x,y,t,b;
};
void bfs(){queue<node>q;q.push(node{sx,sy,0,6});vis[sx][sy]=6;.//这个别忘了while(!q.empty()){int ax=q.front().x,ay=q.front().y;int ab=q.front().b,at=q.front().t;if(ab==0||at>=ans||at>=n*m){q.pop();continue;}if(ma[ax][ay]==4){ab=6;}if(ax==fx&&ay==fy){ans=min(ans,at);q.pop();continue;}for(int i=1;i<=4;i++){int tx=ax+dx[i],ty=ay+dy[i];if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&ab-1>vis[tx][ty]&&ma[tx][ty]!=0){vis[tx][ty]=ab-1;q.push(node{tx,ty,at+1,ab-1});}}q.pop();}//我们重点看这里的回溯位置 就是直接出队然后continue 从而正常出队应该放后面(以前没见过)return ;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&ma[i][j]);if(ma[i][j]==2){ma[i][j]=1;sx=i,sy=j;}if(ma[i][j]==3){ma[i][j]=1;fx=i,fy=j;}}}bfs();if(ans==INF){cout<<-1;}else cout<<ans;system("pause");return 0;
}