0
原题链接:luogu & CF
在任务清单里放了半年,今天终于做出来了 qwq,不得不写题解了。
1
能被 \(11\) 整除的数长什么样子?它的奇数位之和与偶数位之和应当模 \(11\) 同余。
我们不妨把一个数的价值定为从前往后奇数位之和减去偶数位之和模 \(11\) 的值。例如,我们把 114514 的值赋为 \((1+4+1)-(1+5+4)=7\)。
整个序列大概是这样的(画的好丑啊,不想改了):
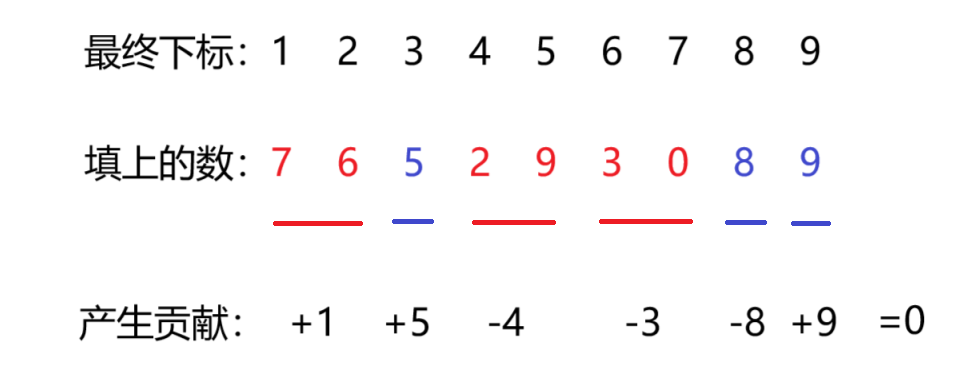
一个数的价值对于整个序列拼成的数的价值会有什么贡献呢?可能为 \(+x\),也可能为 \(-x\),这取决于这个数在序列中的起始位置的奇偶性。比如图中起始下标为 \(1,3,9\) 的数 \(76,5,9\) 产生了正贡献。
为了方便,我们称奇位的数为“奇数”(如 \(5,233,1234567\) 等,图中标蓝),偶位的数为“偶数”。容易发现,如果这个数是“奇数”,排在他之后的元素正负性要反转一下,如果是“偶数”则不变。于是我们先填“奇数”,把“偶数”填在空位里就好。
后面就是计算了。产生正贡献的“奇数”数量是一定的(这应该挺显然的,等于“奇数”数量除以二向上取整),“偶数”则不一定。为了让价值加起来的结果为 \(0\)(这样才能被 \(11\) 整除),我们考虑对两者分别 dp。
记 \(f_{i,j,k}\) 表示前 \(i\) 个“奇数”,其中选了 \(j\) 个产生正贡献(相应地有 \(i-j\) 个产生负贡献),目前的总价值 \(\bmod 11 =k\),这样的排列数有多少个。分这个数选正还是选负转移即可,从 \(i-1\) 转移到 \(i\) 时,空位数就是填正空位的 \(j\) 或者填负空位的 \(i-j\)。
接下来是对“偶数”的 dp,记 \(g_{i,j,k}\) 意义同上。这里需要提前计算空位数量,填完“奇数”后排列就形成了一个“框架”,其中空位数为“奇数”数量加一,产生正贡献的空位和负贡献的空位交错排列。之后每在正空位填一个“偶数”,正空位数就会多一个(可以填在这个“偶数”的左边和右边)。同样的,填入“偶数”的数量我们已经记在状态里了,就是 \(j\)。负空位反之。
最后我们统计答案,如果有 \(x\) 个奇数,\(y\) 个偶数,枚举 \(f_{x,\lceil \frac{x}{2} \rceil,k1}\) 中的 \(k1\),\(g_{y,j,k2}\) 中的 \(j\) 和 \(k2\),如果 \(k_1+k+2 \bmod 11 =0\),就能对答案产生二者相乘的贡献。
然后我们就做完了。
2
代码感觉完全看不了啊。dp 数组大小有点危险,滚了一下。
constexpr int _=2005,B=10,M=11,mod=998244353;
void P(int&x,int y){if((x+=y)>=mod)x-=mod;}
int n;
std::vector<int>a,b;
int jishugeshu,oushugeshu,zhengshuliang,fushuliang,zhengkongwei,fukongwei;
int f[2][_][11],cf,g[2][_][11],cg,ans;
void solve(){rd(n);a.clear();b.clear();for(int i=1,x;i<=n;i++){rd(x);int val=0,j;for(j=1;x;j++,x/=B){if(j&1)val+=x%B;else val-=x%B;}val%=M;if(val<0)val+=M;if(j&1)b.push_back(M-val);else a.push_back(val);}jishugeshu=a.size();oushugeshu=b.size();cf=0;memset(f[cf],0,sizeof f[cf]);f[cf][0][0]=1;for(int i=1,v;i<=jishugeshu;i++){cf^=1;v=a[i-1];memset(f[cf],0,sizeof f[cf]);for(int j=1;j<=i;j++)for(int k=0;k<M;k++)P(f[cf][j][(k+v)%M],f[cf^1][j-1][k]);for(int j=0;j<i;j++)for(int k=0;k<M;k++)P(f[cf][j][k],f[cf^1][j][(k+v)%M]);}//这里的转移没有计算填了哪一个位置,提到外面去了 zhengkongwei=jishugeshu/2+1;fukongwei=jishugeshu+1-zhengkongwei;cg=0;memset(g[cg],0,sizeof g[cg]);g[cg][0][0]=1;for(int i=1,v;i<=oushugeshu;i++){cg^=1;v=b[i-1];memset(g[cg],0,sizeof g[cg]);for(int j=1;j<=i;j++)for(int k=0;k<M;k++)P(g[cg][j][(k+v)%M],1ll*g[cg^1][j-1][k]*(zhengkongwei+j-1)%mod);for(int j=0;j<i;j++)for(int k=0;k<M;k++)P(g[cg][j][k],1ll*g[cg^1][j][(k+v)%M]*(fukongwei+i-1-j)%mod);}fushuliang=jishugeshu/2;zhengshuliang=jishugeshu-fushuliang;ans=0;for(int i=0;i<=oushugeshu;i++){P(ans,1ll*f[cf][zhengshuliang][0]*g[cg][i][0]%mod);for(int j=1;j<M;j++)P(ans,1ll*f[cf][zhengshuliang][j]*g[cg][i][M-j]%mod);}for(int i=1;i<=zhengshuliang;i++)ans=1ll*ans*i%mod;for(int i=1;i<=fushuliang;i++)ans=1ll*ans*i%mod;//这里因为奇数的正负数量已经确定了,枚举排列就放到这里了 printf("%d\n",ans);
}
int main(){int T;rd(T);for(;T;T--)solve();
}