\(\newcommand{\l}{\lambda}\)在之前的讨论中,我们用等号\(=\)表示“可以演算得到”,并且规定等号具有自反、对称、传递的基本性质。这就意味着,我们不仅可以说\((\l x.xx)N\)能演算得到\(NN\),根据对称性也可以说\(NN\)能演算得到\((\l x.xx)N\)。后者听上去很奇怪,因为与其说是“演算”,后者更像是一种“构造”。作为演算规则的\(\beta\)-conversion事实上不应该具有对称性,因为它总是倾向于将\(\l\)-term“化简”。因此我们意识到,对于何为“演算得到”(以及何为“化简”)还没有得到严格的定义。我们应当严格定义一个集合\(\Lambda\)上的二元关系,来描述“演算”(“化简”)。
归约(Reduction)
\(\newcommand{\ttob}{\twoheadrightarrow_\beta}\newcommand{\tob}{\rightarrow_\beta}\newcommand{\eqb}{=_\beta}\)如果我们把\(\alpha\)-equivalance看作语法上的设定(convention),也即我们总是避免局部变量与全局变量的重名,那么\(\l\)-calculus中唯一的演算规则就是\(\l\)-term整体或某一局部的\(\beta\)-conversion。我们定义符号\(\tob\)表示“单步\(\beta\)-reduction”:
- 对任意的\(\l\)-term \(M,N\)和变量\(x\),\((\l x.M)M\tob M[x:=N]\);
- 对任意的\(\l\)-term \(M,N,Z\),如果\(M\tob N\),那么\(ZM\tob ZN\);
- 对任意的\(\l\)-term \(M,N,Z\),如果\(M\tob N\),那么\(MZ\tob NZ\);
- 对任意的\(\l\)-term \(M,N\)和变量\(x\),如果\(M\tob N\),那么\(\l x.M\tob \l x.N\);
基于单步\(\beta\)-reduction,可以定义多步\(\beta\)-reduction(或简称\(\beta\)-reduction),用符号\(\ttob\)表示(多步包括0步):
- 对任意的\(\l\)-term \(M\),\(M\ttob M\);(0步)
- 对任意的\(\l\)-term \(M,N\),如果\(M\tob N\),那么\(M\ttob N\);(单步)
- 对任意的\(\l\)-term \(M,N,L\),如果\(M\ttob N,N\ttob L\),那么\(M\ttob L\);
原先定义的包含对称性的等号现在可以基于\(\beta\)-reduction定义如下,为了看上去更清晰我们用符号\(\eqb\)代替\(=\)(它们的含义是等价的),称为\(\beta\)-conversion:
- 对任意的\(\l\)-term \(M,N\),如果\(M\ttob N\),那么\(M\eqb N\);
- 对任意的\(\l\)-term \(M,N\),如果\(M \eqb N\),那么\(N\eqb M\);(单步)
- 对任意的\(\l\)-term \(M,N,L\),如果\(M\eqb N,N\eqb L\),那么\(M\eqb L\);
可以看到,\(\beta\)-conversion满足自反、对称、传递,是\(\Lambda\)上的等价关系。多步\(\beta\)-reduction只满足自反和传递而不满足对称,这样的关系称为congruence关系。
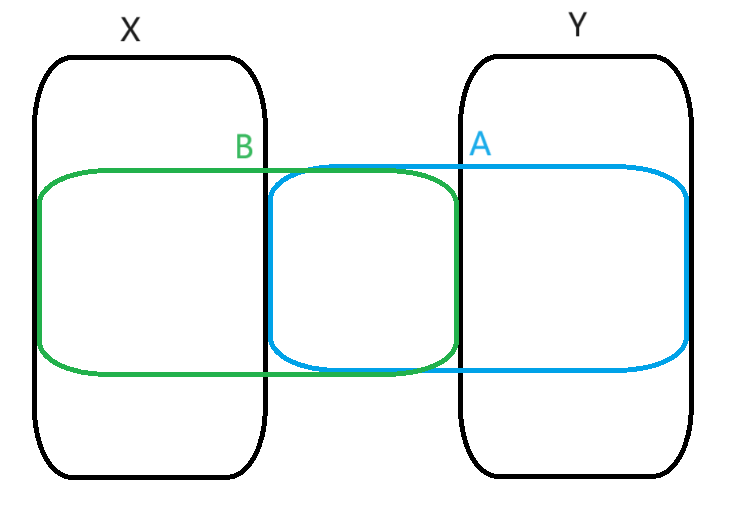
下面的图片清晰展示了\(\beta\)-reduction和\(\beta\)-conversion之间的区别:图中一个箭头表示单步\(\beta\)-reduction,同一直线上的箭头可以连成一个多步\(\beta\)-reduction,而只要忽略箭头方向两个点之间连通就可以满足\(\beta\)-conversion。