D. 超进化：冒泡排序

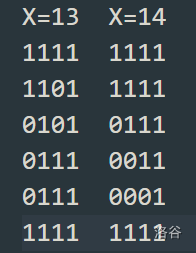
• 【观察性质】
• 冒泡排序的性质：
• 经过 i 次扫描后，数列的末尾 i 项必然是最大的 i 项
• 每⼀轮，每个位置的值最多往前移动⼀位
• 因⽽，冒泡排序k轮以后，第1个位置必定是前k+1个位置中最⼩的，第2个位置必定是前k+2个位置中，除去第1个位置现在的数字外，最⼩的，后续同理。可以用堆维护
• 【分析过程】
• 不断讨论细节会把自己弄晕的！拒绝晕倒，尝试使用数学符号
• 一轮排序后的序列状态是：
• \(min(a_1,a_2),min(max(a_1,a_2),a_3),min(max(a_1,a_2,a_3),a4),...,max(a_1,a_2,...,a_n)\)
• 两轮排序后的序列状态是：
• \(min(a_1,a_2,a_3),min(max(min(a_1,a_2),min(max(a_1,a_2),a_3)),min(max(a_1,a_2,a_3),a4))\)
• 分析\(min(max(min(a_1,a_2),min(max(a_1,a_2),a_3)),min(max(a_1,a_2,a_3),a4))\)
• =\(min(rank_2(a1,a2,a3),min(max(a_1,a_2,a_3),a4))\) 【不妨设\(a_1<a_2<a_3\)】
• =\(min(a_2,min(a_3,a_4))\)=\(min(a_2,a_3,a_4)\) 也可以分析出结果

#include <bits/stdc++.h>
using namespace std;
int a[200005],b[200005];
priority_queue<int,vector<int>,greater<int> >q;
int main()
{ios::sync_with_stdio(false);cin.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}int T;cin>>T;while(T--){long long k;cin>>k;for(int i=1;i<=k/(n-1)+1&&i<=n;i++){q.push(a[i]);}int i=1;while(i<=n){b[i]=q.top();q.pop();if(i+k/(n-1)+1<=n){q.push(a[i+k/(n-1)+1]);}i++;}for(int j=1;j<=k%(n-1);j++){if(b[j]>b[j+1]){swap(b[j],b[j+1]);}}for(int i=1;i<=n;i++){cout<<b[i]<<" ";}cout<<endl;}return 0;
}