手搓指数函数实现

1.概况

最近博主有使用指数函数的需求，需要一条在第一象限、底数为10的曲线。但是由于芯片资源有限，所以无法使用数学库。不能调用数学库里面的指数函数。于是就在网上找了一圈，发现毫无质量。
1.只考虑到了整数次幂的简单情况。

2.要么就是调用数学库，没有一个有用的。

于是打算自己手搓一个指数函数。

2.算法

首先要想实现指数函数，我们需要知道怎么去计算指数函数。简单的比如 10¹ = 10

10² = 10 * 10 =100

10³ = 10* 10 * 10 = 1000
倘若我拿出小数次幂，阁下又该如何应对。
比如：10^0.001的值是多少？

10^0.001 = ?

e^lna = a

10^0.001 = e^{ln2 0.001}

泰勒展开公式：e^x =
e^x=1+x\frac1!+x^2/2!+x3/3!+⋯,-∞<x<∞

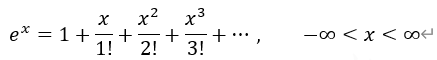
3.代码实现示例

float pow(float x, int y) 
{if (y == 0)return 1;float result = 1.0;int i;for (i = 0; i < y; i++) {result *= x;}return result;
}int factorial(int y) {if (y == 0)return 1;float result = 1.0;int i;for (i = 1; i <= y; i++) {result *= i;}return result;
}float my_pow10(float z)
{int intPart = (int)z;float fractionalPart = z - intPart;float intResult = 1;float ln10_value = 2.302585;float fff;fff = ln10_value *fractionalPart;intResult+= fff;for (int i=2;i<=12;i++){ intResult+= pow(fff,i)/jie(i);}return intResult*pow(10,intPart);
}

3.1.代码解析

此代码示例只是博主为了实现自己需求求以10为底的在第一象限的指数曲线，仅供参考，大家若有其他指数需求可模仿开发

3.1.1计算原理

参数从my_pow10中输入（0~无穷），
根据指数法则：10^a * 10^b = 10^(a+b)将传入的参数分为整数部分和小数部分。小数部分值用函数factorial计算泰勒展开值。整数部分用函数pow计算。最终将两部分值相乘输出。

3.1.2计算精度控制

代码中精度控制为代码中的循环次数，若循环次数更多则结果更逼近最终结果，博主这里精度算到12以满足，如需要更高精度，修改这里的循环次数即可。

for (int i=2;i<=12;i++)
{ intResult+= power1(fff,i)/jie(i);
}

4.总结

本文博主示范了以10为底的指数函数实现，若实现其他为底的，可以模仿这个实现。能实现小数次幂的指数计算，可以说泰勒展开真的是功不可没。很难想象在还没有泰勒展开以前人们对求小数次幂毫无办法。膜拜这些伟大的数学家。