P1220关路灯双log

加强版。课上讲到的经典例题，以下的时空 \(\mathcal O(n\log^2 V)\) 做法（\(V\) 为路灯位置值域）理论上是人尽皆知的，但是全网搜不到这么搞的题解，估计是这题太久远了。传统区间 DP 无法规避两维状态的问题在于，每次折返/拓展时要用新增时间计算两侧灯消耗的额外能量。考虑压缩状态，能否每次只计算一侧灯的消耗？直观来看，画出人关路灯的 \(t-x\) 图像（横轴为数轴上位置，纵轴时间；图丑见谅）：

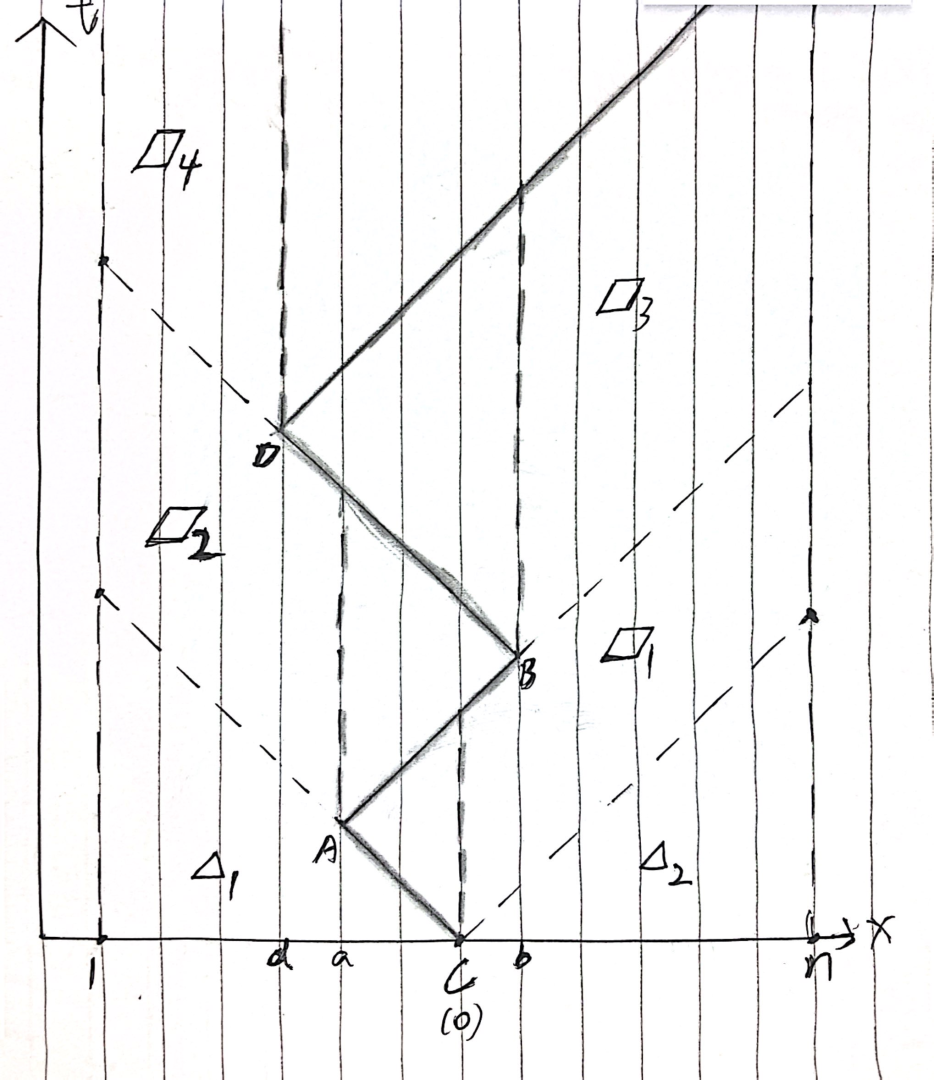
令第 \(i\) 盏灯坐标 \(a_i\)，图像与 \(x=a_i\) 有交的最低纵坐标 \(y_i\)，总能量消耗即为 \(\sum w_iy_i\)。那么考虑如图把图像与 \(x\) 轴围成的区域拆成最下方的两个三角（基础能耗）以及每次折返造成的平行四边形（额外能耗），模拟整个走路过程，在折返时把额外能耗加上以该点为顶点的平四“面积”（\(h\times \sum w_i\)）。

这是一个最短路问题。定义 \(f_i\) 表示，在熄灭 \(i\) 时获得分身，能够从 \(i\) 同时前往 \(1\) 和 \(n\) 并熄灭一路上的所有灯，造成额外能耗的最小值，答案即为 \(\min(f_1,f_n)\) 加上基础能耗。定义比较抽象，但是结合图像和贡献方式是好理解的，如图中 \(f_b\) 由 \(f_a+\Diamond_2\) 转移而来，其值为 \(\Diamond_1+\Diamond_2\)。那么最短路边权式子容易写出：

\[W(i,j)=2(a_j-a_i)\sum_{k<i}w_k\quad(i\le c,j>c) \]

\(i\ge c,j<c\) 的情况同理。边有 \(\Theta(n^2)\) 条不能直接跑，但还是考虑 Dijkstra 的过程，初始确定 \(f_c=0\)，每次取出 \(f_{\min}\) 进行松弛。首先 \(\min\) 从哪来？显然 \(f_i>f_{i+1}(i<c),f_i>f_{i-1}(i>c)\)，那么你实际上就是对 \(f_c,\cdots,f_1\) 与 \(f_c,\cdots,f_n\) 做归并，维护两个指针分别向左向右跑即可。其次如何松弛？上面式子就是在平面上加一条线段 \(\large y=\left(2\sum_{k<i}w_k\right)x-2a_i\sum_{k<i}w_k\)，用它去更新所有线段中与 \(x=a_j\) 最靠下的交点，那么上李超线段树即可。

因为值域大要动态开点，所以空间也是 \(\log^2\) 的略显难受。不过线段的左右端点只有两种情况，应该有更优的实现。核心思路就是将两边目前必需的能耗写进一维状态，从而做到一次决策只用计算一边，虽然转移函数仍然是二元的，但是和另外一边呈线性关系，就可以转化为平面上的问题。另外，不知道能不能扩展到ABC219H。

#include <cstdio>
#include <algorithm>
#define ll long longusing namespace std;const int N=5141;int O;struct lin{ll k,b;ll val(int x){return k*(x>O?x-O:O-x)+b;}
};namespace sgt{struct node{int ls,rs;#define ls(x) t[x].ls#define rs(x) t[x].rs}t[N*100];lin g[N*100];int tot=1;int req(int &x){return x?x:x=++tot;}void dnf(int now,int ln,int rn,lin f){if(!g[now].k) return g[now]=f,void();int mid=ln+rn>>1;if(f.val(mid)<g[now].val(mid)) swap(f,g[now]);if(ln==rn) return ;if(f.val(ln)<g[now].val(ln)) dnf(req(ls(now)),ln,mid,f);if(f.val(rn)<g[now].val(rn)) dnf(req(rs(now)),mid+1,rn,f);}void upd(int now,int ln,int rn,int l,int r,lin f){if(l<=ln&&rn<=r) return dnf(now,ln,rn,f);int mid=ln+rn>>1;if(l<=mid) upd(req(ls(now)),ln,mid,l,r,f);if(r>mid) upd(req(rs(now)),mid+1,rn,l,r,f);}ll qry(int now,int ln,int rn,int k){ll res=g[now].k?g[now].val(k):1e18;if(ln==rn) return res;int mid=ln+rn>>1;if(k<=mid) res=min(res,qry(ls(now),ln,mid,k));else res=min(res,qry(rs(now),mid+1,rn,k));return res;}
}using namespace sgt;int a[N];ll w[N];//#include "xzr.hpp"int main()
{//wxd;//Xzr;int n,o;scanf("%d%d",&n,&o);for(int i=1;i<=n;++i) scanf("%d%lld",a+i,w+i);O=a[o];long long ans=0;int V=a[n];for(int i=1;i<o;++i) ans+=(O-a[i])*w[i],w[i]+=w[i-1];for(int i=n;i>o;--i) ans+=(a[i]-O)*w[i],w[i]+=w[i+1];upd(1,1,V,O,V,{2*w[o-1],0});upd(1,1,V,1,O,{2*w[o+1],0});for(int l=o-1,r=o+1;l||r<=n;){ll L=l?qry(1,1,V,a[l]):1e18,R=r<=n?qry(1,1,V,a[r]):1e18;if(L<R) upd(1,1,V,O,V,{2*w[l-1],2*(O-a[l])*w[l-1]+L}),--l;else upd(1,1,V,1,O,{2*w[r+1],2*(a[r]-O)*w[r+1]+R}),++r;}printf("%lld",ans+min(qry(1,1,V,a[1]),qry(1,1,V,a[n])));
}