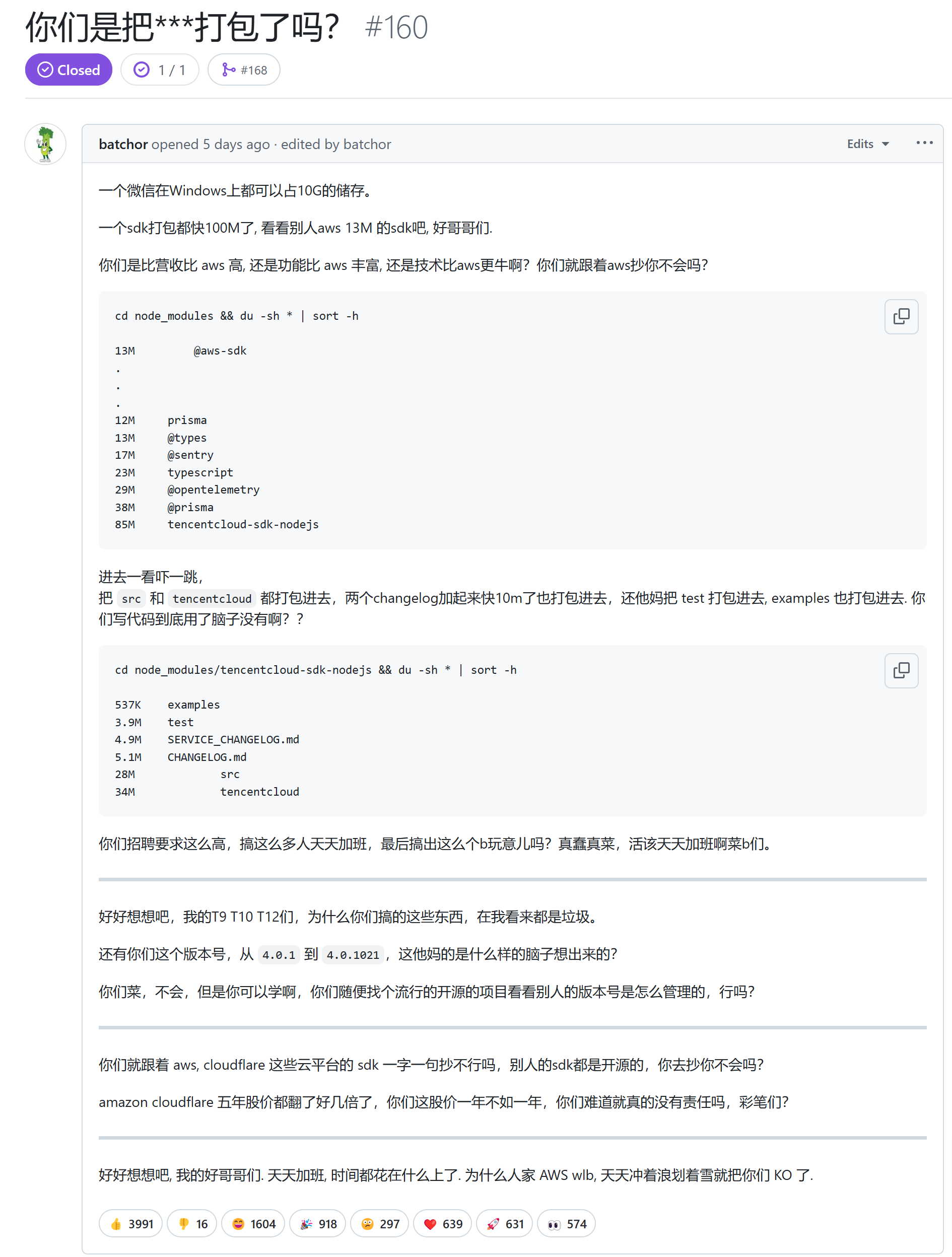
Solution
题意
原题链接
定义二元关系 \(\text{S}\),其满足反对称性且不满足传递性。
现有互异元素 \(N(N \le 1000)\) 个,可以进行不多于 \(10000\) 次提问,每次提问可以得知两指定元素 \(a,b\) 的 \(a \, \text{S} \, b\) 结果。求序列 \(a_N\) 满足:对任意 \(x_i,x_{i+1} \in a_N\),有 \(x_i \, \text{S} \, x_{i+1}\)。
解释一下:
反对称性:对集合 \(X\) 上的二元关系 \(\text{S}\),对任意 \(x_1,x_2 \in X(x_1 \ne x_2)\),若 \(x_1 \, \text{S} \, x_2\),则 \(x_2 \, \text{S} \, x_1\) 不成立。
例如:“小于”是实数集上的二元关系,它满足反对称性,即有:对任意 \(x_1,x_2 \in R(x_1 \ne x_2)\),若 \(x_1 < x_2\),则 \(x_2 <x_1\) 不成立。
传递性:对集合 \(X\) 上的二元关系 \(\text{S}\),对任意 \(a,b,c \in X\)(\(a,b,c\) 互不相等),若 \(a \, \text{S} \, b\) 且 \(b \, \text{S} \, c\),则有 \(a \, \text{S} \, c\) 成立。
例如:“小于”是实数集上的二元关系,它满足传递性,即有:对任意 \(a,b,c \in R\)(\(a,b,c\) 互不相等),若 \(a<b\) 且 \(b<c\),则有 \(a<c\) 成立。
由此可见,本题题面所述“小于”并非正常理解的小于,而是一种比较特殊的二元关系。基于图的思想和题目提示,我们可以尝试用图转化问题:
元素->节点 \(\hspace{1.5cm}\) 二元关系 \(\text{S}\)->边(\(a \, \text{S} \, b\) 为真->有一条从 \(a\) 到 \(b\) 的有向边)
满足反对称性->没有无向边 \(\hspace{1.5cm}\) 不满足传递性->要求最终结果为链
所以,原题即为:在只能得知指定的 \(10000\) 条边的有向完全图(或称竞赛图)中找一条 \(\text{Hamilton}\) 路径。
分析
1.有向完全图一定存在 \(\text{Hamilton}\) 路径的证明(可跳过)
为了论述的严谨性,我们先证明有向完全图一定存在 \(\text{Hamilton}\) 路径。(当然,可以直接从百度百科找定理秒,百科链接)
以下是一个自认比较简单,十分粗糙但相对好懂的证明(若有不完备还请指出):
考虑归纳法:
设有一个 \(n(n \ge 2)\) 阶有向完全图。
\(n =2\),显然成立;
设 \(n=k\) 时成立,对 \(n=k+1\),考虑如何添加一个点:
(如图,只画了 \(6\) 个点,但假设中间还有很多点,除了 \(\text{Hamilton}\) 路径和 $ <1,6> $ 间的边外的边省略)
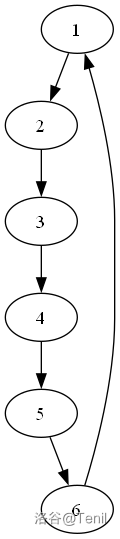
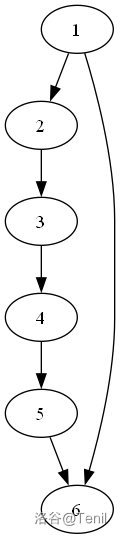
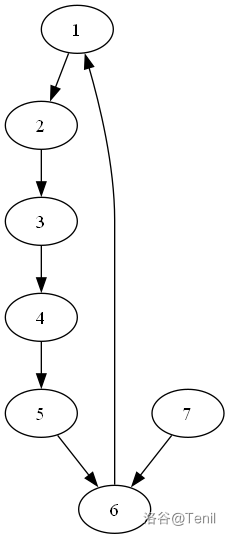

\(\hspace{1cm}\) 图1(顺接) \(\hspace{0.5cm}\) 图2(逆接) \(\hspace{1.5cm}\) 图3 \(\hspace{3cm}\) 图4
现在考虑一下链首尾连接的情况:对于图1这种成环的情况(情况 A),任意一点以任意取向都可以接入(如图3(7-6-1-2-3-4-5)图4(1-2-3-4-5-6-7)),直接不用看。重点是不成环的。

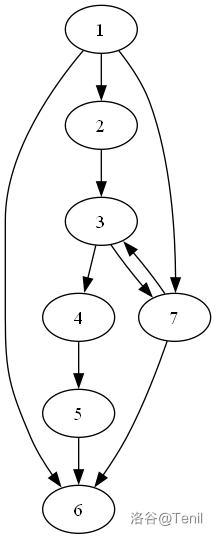
对左图情况,若新加点连边为 $ <8,1> $ 或 $ <6,7>$,则直接成立(情况 B);若为右图情况,考虑链上任意一点(此例为 3),若 3 与 7 之间连边为 $ ❤️,7> $,则 3,4,5,6,7 部分与整体形似,可以类似上述考虑方式地分隔,直至达成情况 A 或情况 B,或者分隔出的联通块阶数为 2,一定成立。 3 与 7 之间连边为 $ <7,3> $ 同理。
于是 \(n=k+1\) 时成立,故结论得证。
2.算法思路
根据上述论述过程,我们也能够得到一种方法:在已有链上插入新加点,在不能直接接上链头和链尾时,可以枚举中间某点缩小一定存在可以插入处的链范围。于是我们可以想到一种形似二分的写法:每次插入新点时,提问 \(mid=(l+r) \div 2\) 与新加点的边的取向,从而确定某部分一定有可插入处,缩小范围直至确定,然后直接插入即可。
预计最大提问次数为 \(\sum_{i=1}^N {log_2i} \approx 8529<10000\),而且貌似数据比较弱,既是每次都先枚举 \(l,r\) 最大提问次数约 \(4+\sum_{i=3}^N {[log_2(i-2)+2]} \approx 10513>10000\) 也能过(笑)。
不算插入的话时间复杂度为 \(Θ(nlogn)\),数组暴力插入,于是成了 \(Θ(n^2)\)。但对于 \(N \le 1000\) 也是绰绰有余了。
实现
先选两个点进数组,然后进行拓展:每次拓展选取数组内现有数的中间一个,和新加点进行提问,根据方向缩小区间,直至可以直接连入时,暴力连入即可。
Code
#include <iostream>
#include <cstdio>
#include <cctype>using namespace std;typedef long long ll;ll fr() {ll x=0,f=1;char c=getchar();while(!isdigit(c)) {if(c=='-') f=-1;c=getchar();}while(isdigit(c)) {x=(x<<3)+(x<<1)+(c^48);c=getchar();}return x*f;
}//只读一个也要写快读的屑bool compare(int a, int b)
{cout << "? " << a << ' ' << b << endl;bool t;cin >> t;return t;
}const int maxn=1e3+100;
ll n,ans[maxn];int main(){n=fr();ans[1]=1;for(register int i = 2; i <= n; i++){if(compare(i,ans[1])) {for(register int j = i; j > 1; j--) {ans[j]=ans[j-1];}ans[1]=i;}else{int l=1,r=i;while(l+1 < r){//逆天边界,卡我2.5年int mid=(l+r)>>1;if(compare(i,ans[mid])){r=mid;}else{l=mid;}}for(register int j = i; j > r; j--) {ans[j]=ans[j-1];}ans[r]=i;}}printf("!");for(register int i = 1; i <= n; i++) printf(" %lld",ans[i]);return 0;
}
闲话
如果觉得有用,还请点个赞吧!