A. Tokitsukaze and Absolute Expectation
待补
B. Tokitsukaze and Balance String (easy) && C. Tokitsukaze and Balance String (hard)
题意:给你一个01串,有些地方是'?'表示没有填。一个01串的价值看它有多少位置满足取反后整个串10和01的个数相等。求所有可能的01串的价值之和。
这题正解是找规律分类讨论,赛时没多想写了个dp。
手玩一下发现,中间的位置不管怎么变都不会影响10和01的个数。于是如果这个01串本来就是平衡的则贡献为\(n-2\)。然后10的个数和01的个数差值的绝对值不超过1,因为你一个一个往后填01发现,两个01必然贡献一个10,两个10必然贡献一个01。赛时我也是根据这个性质进行的dp。然后发现如果\(s_1 == s_n\)则10和01的个数相等,进行分类讨论就行。中间\(n-2\)个产生的贡献是固定的。
讲讲我的dp解法,\(f[i][0/1][-1/0/1]\),表示第\(i\)个位置填\(0/1\)并且10个数减01个数为\(-1/0/1\)时的方案数,那么答案就是\((f[n][0][0] + f[n][1][0]) \times 2\),然后如果\(s_1 != 0\), 发现只要变化一定使得差值减一,则加上\(f[n][0][1] + f[n][1][1]\),如果\(s_n != 1\),则加上\(f[n][0][0] + f[n][1][0]\),\(s_n\)类似的讨论,其实最后这个讨论就是正解的讨论,我也是写完了才发现\(dp\)了个寂寞。因为有负数下标,第三维都加个1变成\(0/1/2\)。
点击查看代码
void solve() {int n;std::cin >> n;std::string s;std::cin >> s;std::vector f(n + 1, std::array<std::array<Z, 3>, 2>{});if (s[0] == '?') {f[1][0][1] = f[1][1][1] = 1;} else if (s[0] == '0') {f[1][0][1] = 1;} else {f[1][1][1] = 1;}for (int i = 1; i < n; ++ i) {if (s[i] != '0') {f[i + 1][1][0] = f[i][1][0] + f[i][0][1];f[i + 1][1][1] = f[i][1][1] + f[i][0][2];f[i + 1][1][2] = f[i][1][2];} if (s[i] != '1') {f[i + 1][0][0] = f[i][0][0];f[i + 1][0][1] = f[i][0][1] + f[i][1][0];f[i + 1][0][2] = f[i][0][2] + f[i][1][1];}}if (n == 1) {std::cout << (f[n][0][1] + f[n][1][1]) << "\n";return;}Z ans = (f[n][0][1] + f[n][1][1]) * (Z)(n - 2);if (s[0] != '0') {ans += f[n][0][2] + f[n][1][2];}if (s[0] != '1') {ans += f[n][0][0] + f[n][1][0];}if (s.back() != '0') {ans += f[n][0][0] + f[n][1][0];}if (s.back() != '1') {ans += f[n][0][2] + f[n][1][2];}std::cout << ans << "\n";
}
D. Tokitsukaze and Concatenate Palindrome
题意:给你两个字符串\(a, b\),你可以将它们都重新排列然后拼接起来。你还可以修改\(a\)里的元素,求让\(a+b\)是回文最小要修改几次。
因为可以重新排列,那么我们尽可能把相同的字符放到对应的位置。然后长串是可以放一些字符到另一边自己和自己匹配的,于是就是统计一下有多少个字符不能匹配,直接除二。因为两边不能匹配的字符数肯定是相等的。如果是奇数个,那么\(a+b\)长度肯定也是奇数,多出来的可以放中间,答案也是直接除二就行。
点击查看代码
void solve() {int n, m;std::cin >> n >> m;std::string s, t;std::cin >> s >> t;std::array<int, 26> cnt{};for (auto & c : s) {cnt[c - 'a'] += 1;}for (auto & c : t) {cnt[c - 'a'] -= 1;}int ans = 0;int tot = std::max(n, m) - (n + m + 1) / 2;for (int i = 0; i < 26; ++ i) {if (cnt[i] < 0 && n <= m) {cnt[i] = -cnt[i];int t = std::min(tot, cnt[i] / 2);cnt[i] -= t * 2;tot -= t;} else if (cnt[i] > 0 && n >= m) {int t = std::min(tot, cnt[i] / 2);cnt[i] -= t * 2;tot -= t; }}for (int i = 0; i < 26; ++ i) {ans += std::abs(cnt[i]);}std::cout << ans / 2 << "\n";
}
E. Tokitsukaze and Dragon's Breath
题意:给你一个矩阵,可以选择一个位置得到这个位置所处主对角线和次对角线上所有元素的和。求最大值。
每个主对角线的\(i + j\)相等,每个次对角线的\(i - j\)相等,存下来枚举取那个位置的对角线即可。
点击查看代码
void solve() {int n, m;std::cin >> n >> m;std::vector a(n, std::vector<int>(m));std::vector<i64> sum1((n + m) * 2), sum2((n + m) * 2);for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {std::cin >> a[i][j];sum1[i + j + n + m] += a[i][j];sum2[i - j + n + m] += a[i][j];}}i64 ans = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {ans = std::max(ans, sum1[i + j + n + m] + sum2[i - j + n + m] - a[i][j]);}}std::cout << ans << "\n";
}
F. Tokitsukaze and Kth Problem (easy)
待补
G. Tokitsukaze and Kth Problem (hard)
待补
H. Tokitsukaze and Necklace
待补。
I. Tokitsukaze and Pajama Party
题意:求每个"uwawauwa"前面有多少"u"。
模拟统计即可。
点击查看代码
void solve() {int n;std::cin >> n;std::string s;std::cin >> s;std::string t = "uwawauwa";int len = t.size();i64 ans = 0, cnt = 0;for (int i = 0; i + len - 1 < n; ++ i) {if (s.substr(i, len) == t) {ans += cnt;}if (i > 0 && s[i - 1] == 'u') {++ cnt;}}std::cout << ans << "\n";
}
J. Tokitsukaze and Recall
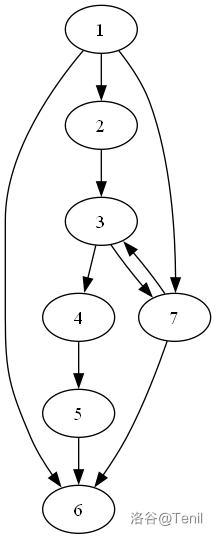
题意:有若干个联通块,你可以选\(k\)个点,可以随时传送到这\(k\)个点的任意一个。你要占领尽可能多的点。并给出移动方案。要求字典序最小。
首先求出所有连通块。设有\(cnt\)个。
要占领尽可能的点,那么我们肯定先联通块大小从大到小的给每个联通块一个传送点,如果大小相同,则最小点更小的优先。然后可以搜索方案,我们给每个联通块最小的点一个传送点,然后我们用优先级队列来搜索使得我们每次可以走编号最小的点。如果还有多余的传送点,并且当前到的点不是可以到的剩余点里的最小的,那么可以给这个剩余点里最小的点一个传送点。模拟即可。
点击查看代码
struct DSU {std::vector<int> fa, cnt;DSU(int _n) {init(_n);}void init(int _n) {fa.assign(_n + 1, 0);cnt.assign(_n + 1, 1);std::iota(fa.begin(), fa.end(), 0);}int find(int x) {return x == fa[x] ? x : fa[x] = find(fa[x]);}bool merge(int x, int y) {x = find(x), y = find(y);if (x == y) {return false;}fa[y] = x;cnt[x] += cnt[y];return true;}bool same(int x, int y) {return find(x) == find(y);}int size(int x) {return cnt[find(x)];}
};void solve() {int n, m, k;std::cin >> n >> m >> k;std::vector<std::vector<int>> adj(n);DSU d(n);for (int i = 0; i < m; ++ i) {int u, v;std::cin >> u >> v;-- u, -- v;if (u > v) {std::swap(u, v);}adj[u].push_back(v);adj[v].push_back(u);d.merge(u, v);}std::vector<std::vector<int>> blocks(n);int cnt = 0;for (int i = 0; i < n; ++ i) {blocks[d.find(i)].push_back(i);cnt += d.find(i) == i;}std::sort(blocks.begin(), blocks.end(), [&](std::vector<int> & a, std::vector<int> & b) {if (a.size() && b.size() && a.size() == b.size()) {return a[0] < b[0];}return a.size() > b.size();});int t = std::min(k, cnt);k = std::max(0, k - cnt);std::priority_queue<int, std::vector<int>, std::greater<int> > heap;std::vector<int> st(n);std::set<int> s;for (int i = 0; i < t; ++ i) {for (auto & x : blocks[i]) {s.insert(x);}heap.push(blocks[i][0]);st[blocks[i][0]] = 1;}std::vector<int> ans;while (heap.size()) {if (heap.top() != *s.begin() && k > 0) {-- k;heap.push(*s.begin());st[*s.begin()] = 1;}int u = heap.top(); heap.pop();s.erase(u);ans.push_back(u);for (auto & v : adj[u]) {if (!st[v]) {st[v] = 1;heap.push(v);}}}std::cout << ans.size() << "\n";for (auto & x : ans) {std::cout << x + 1 << " \n"[x == ans.back()];}
}
K. Tokitsukaze and Shawarma
签到题。
点击查看代码
void solve() {int x, y, z, a, b, c;std::cin >> x >> y >> z >> a >> b >> c;std::cout << std::max({x * a, y * b, z * c}) << "\n";
}
L. Tokitsukaze and XOR-Triangle
题意:多次询问求一个区间内两两异或和的和。
按位计算,那么就变成了在一个01串里询问一个区间里有多少01和10。
可以前缀和求出来每个位置和它前面的数产生了多少贡献。但求\([l, r]\)时,发现\(sum_r - sum_{l-1}\)这个贡献里\([l, r]\)里数算上了\([1, l - 1]\)这些数产生的贡献,考虑减去,设\([1, l - 1]\)有\(cnta0\)个0,\(cnta1\)个1,\([l, r]\)里有\(cntb0\)个0,\(cntb1\)个1。那么需要减去的贡献为\(cnta0 \times cntb1 + cnta1 \times cntb0\)
点击查看代码
void solve() {int n, q;std::cin >> n >> q;std::vector<i64> a(n + 1), b(n + 1);for (int i = 1; i <= n; ++ i) {std::cin >> a[i];}for (int i = 1; i <= n; ++ i) {std::cin >> b[i];}std::vector suma(n + 1, std::array<i64, 30>{});std::vector sumb(n + 1, std::array<i64, 30>{});for (int i = 1; i <= n; ++ i) {suma[i] = suma[i - 1];sumb[i] = sumb[i - 1];for (int j = 0; j < 30; ++ j) {suma[i][j] += a[i] >> j & 1;sumb[i][j] += b[i] >> j & 1;}}std::vector sum(n + 1, std::array<i64, 30>{});for (int i = 1; i <= n; ++ i) {sum[i] = sum[i - 1];for (int j = 0; j < 30; ++ j) {if (b[i] >> j & 1) {sum[i][j] += i - suma[i][j];} else {sum[i][j] += suma[i][j];}}}for (int i = 0; i < q; ++ i) {int l, r;std::cin >> l >> r;Z ans = 0;for (int i = 0; i < 30; ++ i) {i64 cnta1 = suma[l - 1][i], cnta0 = l - 1 - cnta1;i64 cntb1 = sumb[r][i] - sumb[l - 1][i], cntb0 = r - l + 1 - cntb1;ans += (Z)(1ll << i) * (sum[r][i] - sum[l - 1][i] - cnta1 * cntb0 - cnta0 * cntb1);}std::cout << ans << "\n";}
}