ACM寒假集训第三次专题任务
一、Priority Queue
题目:
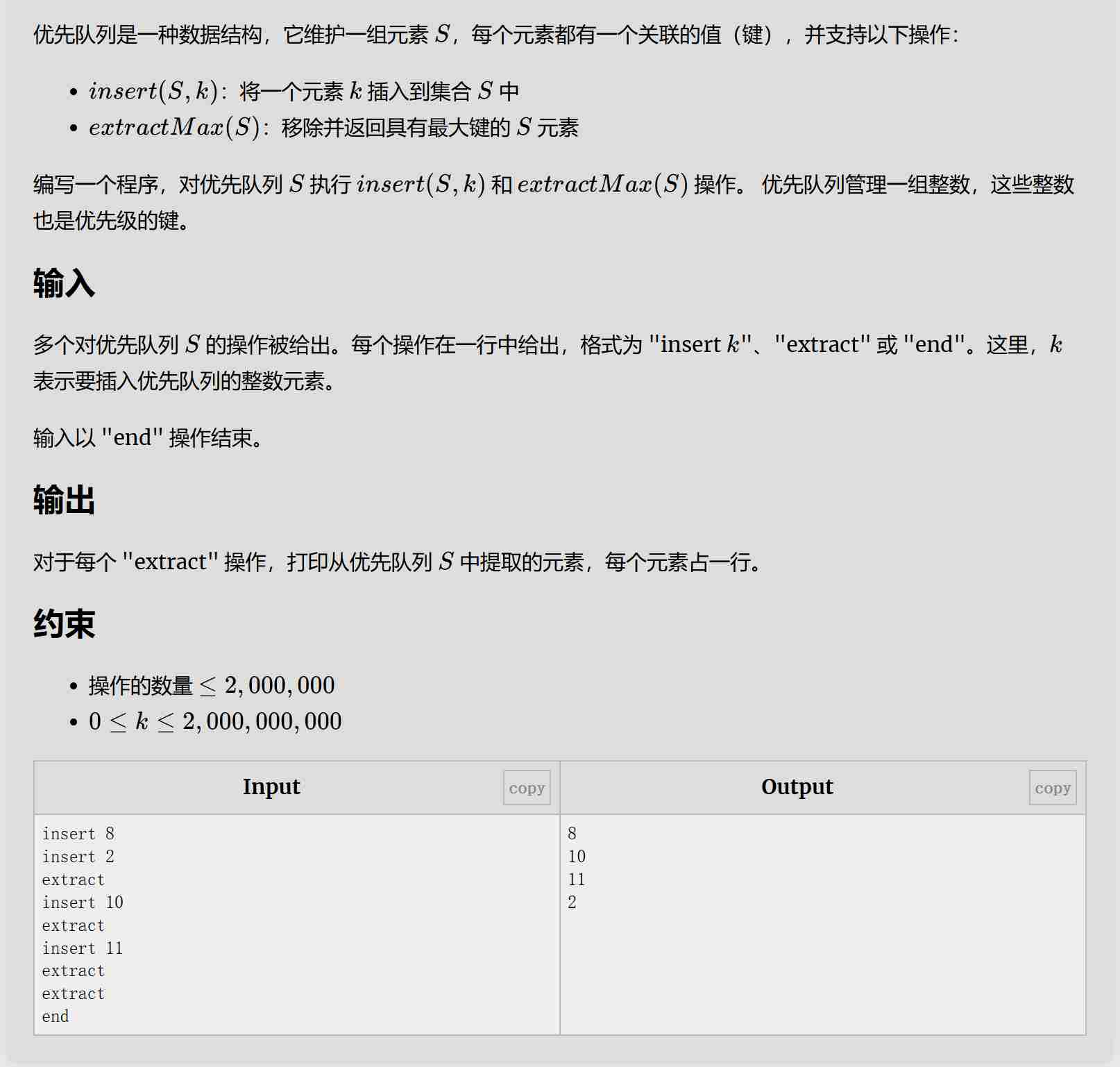
解题思路:
对优先队列的直接运用,直接翻译题目即可。
AC代码:
#include<iostream>
#include<string>
#include<queue>
using namespace std;
int main()
{int k;string operation;priority_queue<int> S;while(1){cin>>operation;if(operation=="insert"){cin>>k;S.push(k);}else if(operation=="extract"){if(!S.empty()){cout<<S.top()<<endl;S.pop();}}else if(operation=="end"){break;}}return 0;
}
二、ST 表 && RMQ 问题
题目:

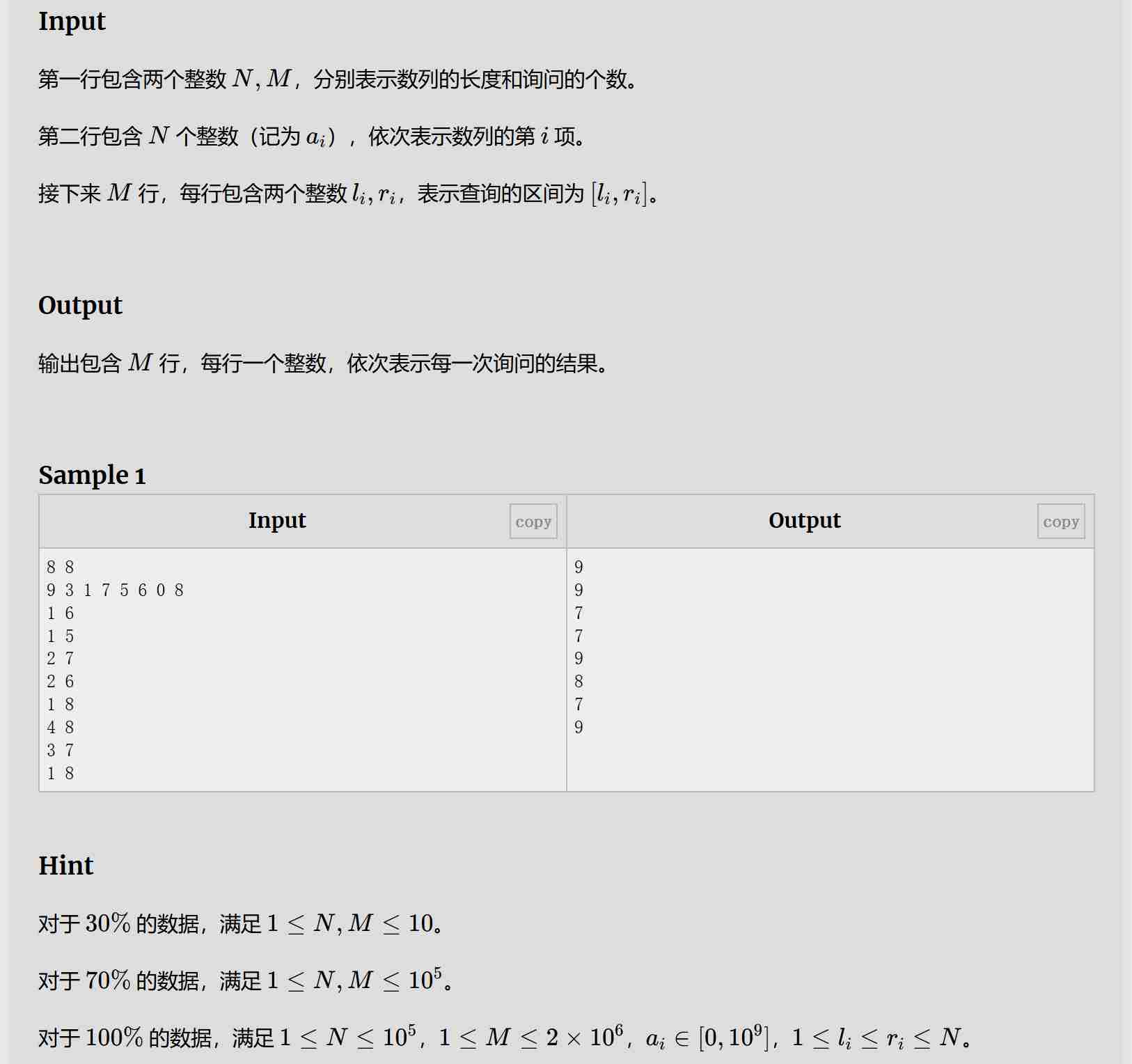
解题思路:
先构建ST表(以Sample 1为例):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| i=0 | 9 | 3 | 1 | 7 | 5 | 6 | 0 | 8 |
| i=1 | 9 | 3 | 7 | 7 | 6 | 6 | 8 | |
| i=2 | 9 | 7 | 7 | 7 | 8 | |||
| i=3 | 9 |
再输入l和r,判断l到r整个区间的长度,取对数得到小于此长度的最大i(2的i次方,例如,9对应i为3,因为2的3次方为8,而8是小于9的。当i取4时则得到16大于9,不合题意)。
然后判断第一段、第二段起末位置并比较大小。
AC代码:
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdio>
using namespace std;
int N,M,l,r,a[31][100005],len;
int main()
{scanf("%d%d",&N,&M);for(int i=1;i<=N;i++){scanf("%d",&a[0][i]);}len=log2(N);for(int i=1;i<=len;i++){for(int j=1;j<=N-(1<<(i-1));j++){a[i][j]=max(a[i-1][j],a[i-1][j+(1<<(i-1))]);}}while(M--){scanf("%d%d",&l,&r);len=log2(r-l+1);printf("%d\n",max(a[len][l],a[len][r-(1<<len)+1]));}return 0;
}
三、合并果子
题目:

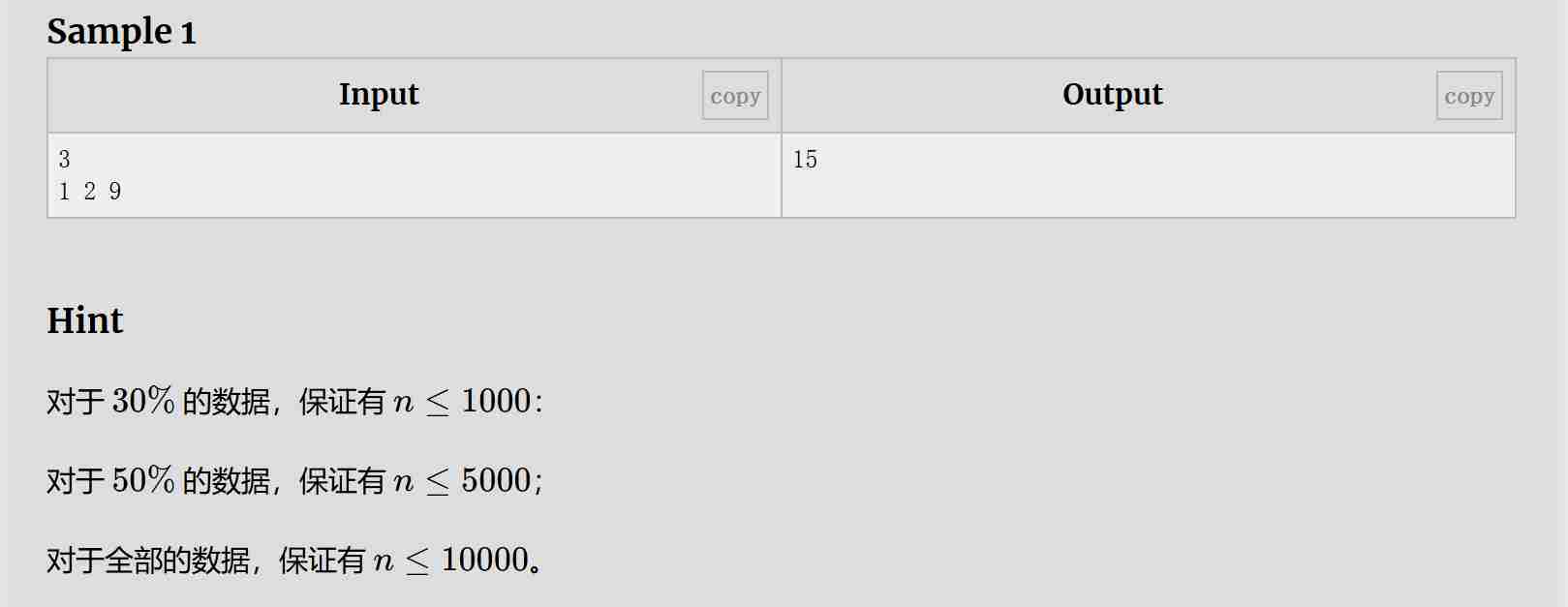
解题思路:
论小根堆的运用,只要把每轮最小的两个加起来并都予去除,再push两者之和进堆即可。
AC代码:
#include<iostream>
#include<queue>
#include<functional>
#include<vector>
using namespace std;
int n,sum,t,k;
priority_queue<int,vector<int>,greater<int>> a;
int main()
{cin>>n;for(int i=0;i<n;i++){cin>>k;a.push(k);}while(a.size()!=1){t=0;t+=a.top();a.pop();t+=a.top();sum+=t;a.pop();a.push(t);}cout<<sum;
}
四、约瑟夫问题
题目:
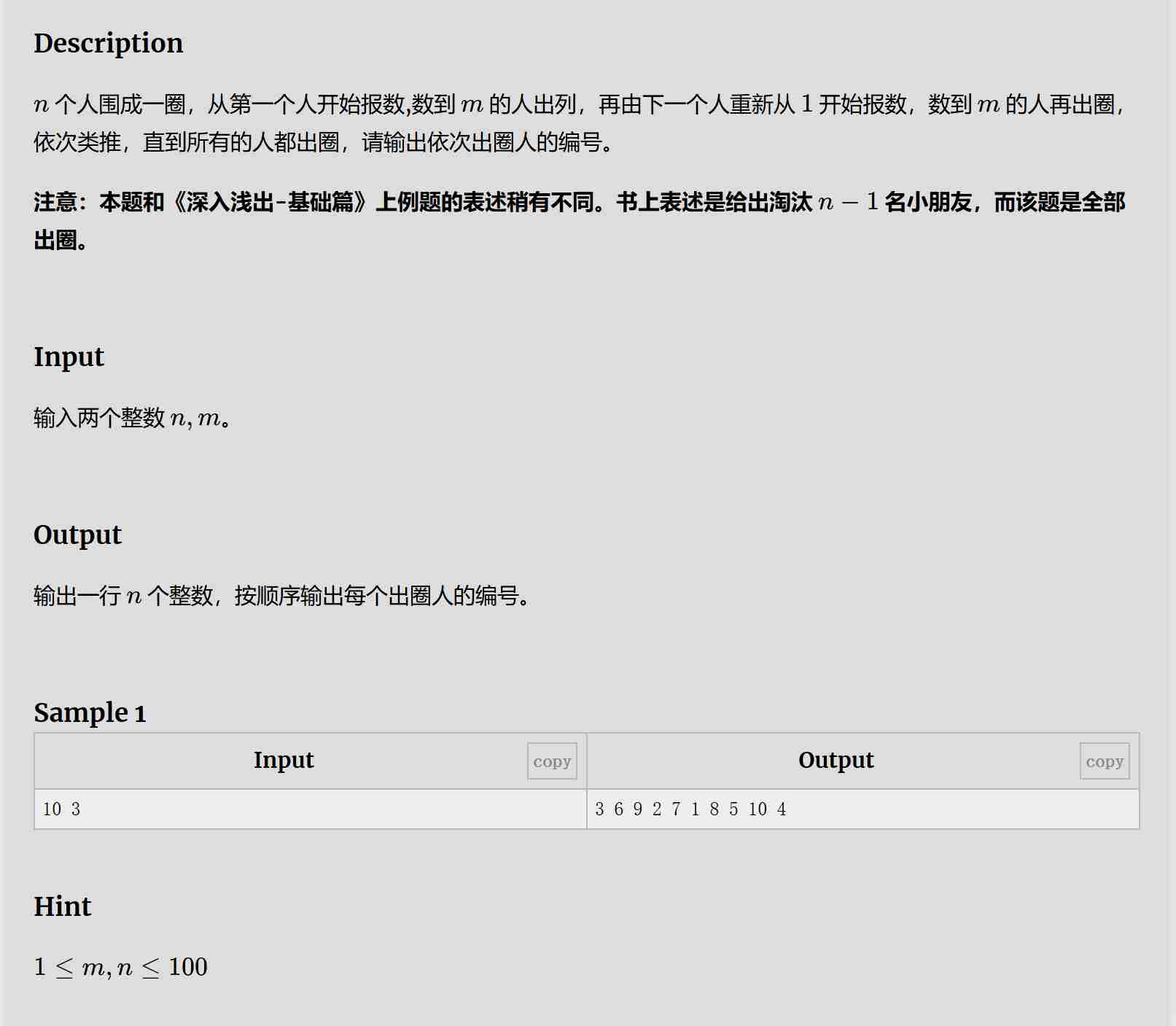
解题思路:
论队列的运用,把跳过的人从队首调到对尾,出圈的人则输出并从队伍中删除。
AC代码:
#include<iostream>
#include<queue>
using namespace std;
int n,m;
queue<int> a;
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){a.push(i);}while(!a.empty()){for(int i=1;i<m;i++){int t=a.front();a.pop();a.push(t);}cout<<a.front()<<" ";a.pop();}return 0;
}
五、Look Up S
题目:

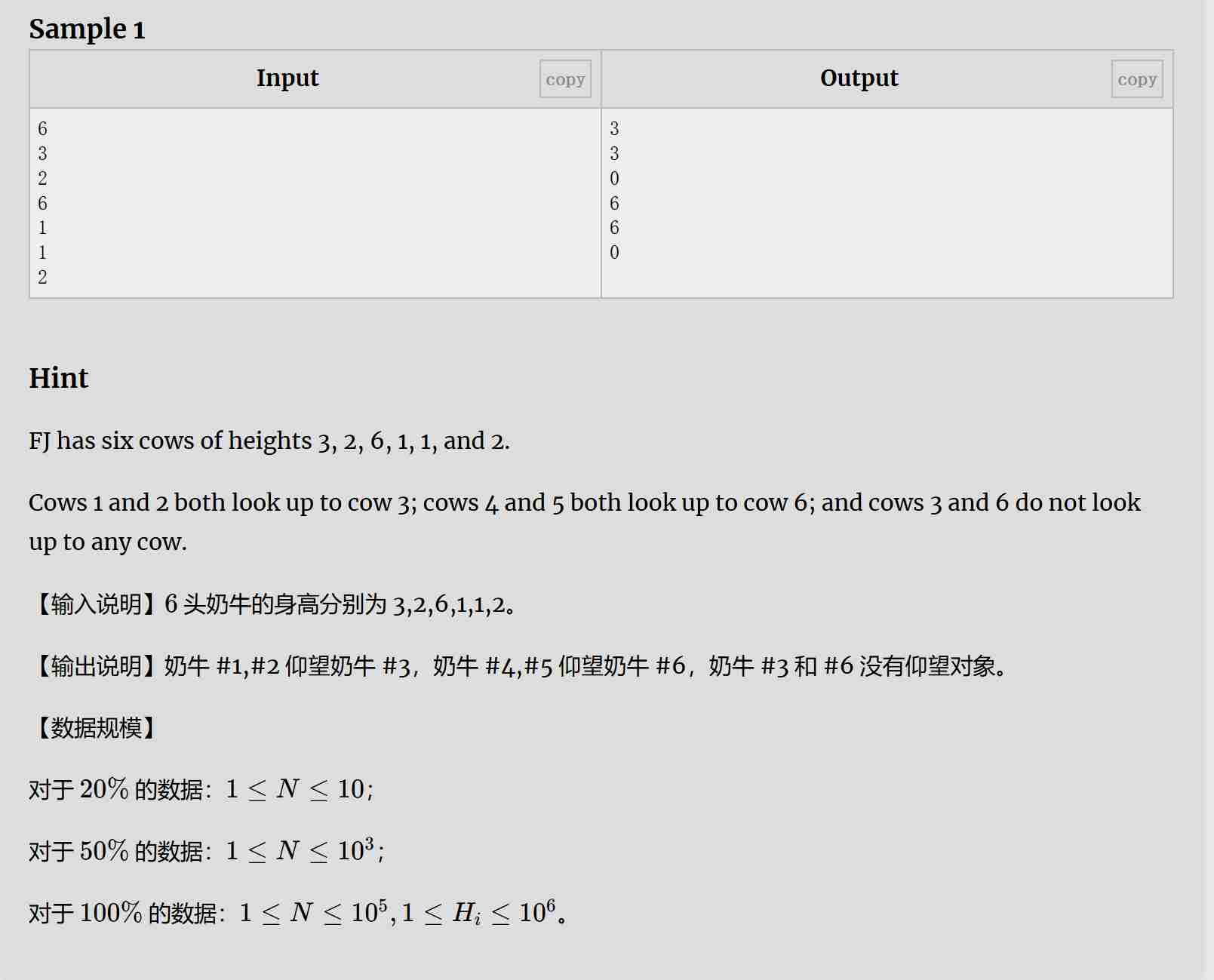
解题思路:
单调栈的运用,相当于一次遍历找所有数的下一最近的大于此数的数的位置。
先把第一个数放进栈,第二个数若比它大,则其为第一个数对应所求;若比它小,则不是,并将第二个数也放进栈。如果第三个数大于第一个数,那么它既为第一个数对应答案也是第二个数对应答案,则将第一个数与第二个数从栈中消去(因为已经找到它们的答案了)。以以上思路进行循环即可得答案。
循环结束后仍在栈中的数则没有对应答案,输出0。
AC代码:
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
struct cow{int h;int code;
};
int main()
{int n;cin>>n;vector<int> v(n+1),ans(n+1,0);stack<cow> s;for(int i=1;i<=n;i++){cin>>v[i];}for(int i=1;i<=n;i++){if(s.empty()||v[i]<=s.top().h){s.push(cow{v[i],i});}else{while(!s.empty()&&v[i]>s.top().h){ans[s.top().code]=i;s.pop();}s.push(cow{v[i],i});}}while(!s.empty()){ans[s.top().code]=0;s.pop();}for(int i=1;i<=n;i++){cout<<ans[i]<<endl;}return 0;
}
六、国旗计划
题目:


解题思路:
环的问题,2倍链处理。结构体输入战士信息。假设对i战士进行分析,其右端点为r[i],那么下一个战士j要符合条件:
-
l[j]≤r[i],保证能够覆盖要求
-
r[j]尽量大,这是为了能够最优
用ST表进行处理
AC代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 2e5 + 5;
int n, m;
int ans[MAXN];
int f[MAXN*2][20];
struct node {int id;int l, r;
} s[MAXN*2];
bool cmp(node a, node b) {return a.l < b.l;
}
void pre() {for (int i = 1, p = i; i <= 2 * n; i++) {while (p <= 2 * n && s[p].l <= s[i].r) {p++;}f[i][0] = p - 1;}for(int i = 1; i < 20; i++) {for(int j = 1; j <= 2 * n; j++) {f[j][i] = f[f[j][i-1]][i-1];}}
}
void solve(int k) {int rr = s[k].l + m;int tot = 1;int p = k;for (int i = 19; i >= 0; i--) {if (f[k][i] != 0 && s[f[k][i]].r < rr) {tot += (1 << i);k = f[k][i];}}ans[s[p].id] = tot + 1;
}
int main(){scanf("%d %d", &n, &m);for (int i = 1; i <= n; i++) {scanf("%d %d", &s[i].l, &s[i].r);if (s[i].r < s[i].l) {s[i].r += m;}s[i].id = i;}sort(s + 1, s + 1 + n, cmp);for(int i = 1; i <= n; i++) {s[i + n] = s[i];s[i + n].l = s[i].l + m;s[i + n].r = s[i].r + m;}pre();for(int i = 1; i <= n; i++) {solve(i);}for(int i = 1; i <= n; i++) {printf("%d ", ans[i]);}return 0;
}
学习总结
学习了一些数据结构
stack
头文件#include <stack>
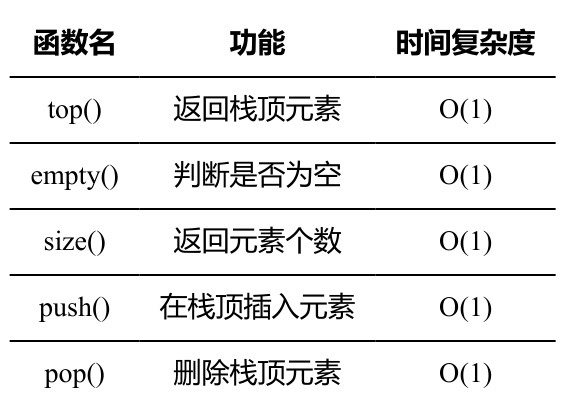
定义:stack<int> s;
queue
头文件#include <queue>


定义:queue<int> q;
priority_queue
头文件#include <queue>

定义:priority_queue<int> q;默认为大根堆
定义小根堆:priority_queue<int, vector<int>,greater<int> > p;
ST表
详细使用见二、ST 表 && RMQ 问题。