浅谈操作分块：从 Div.3 F 到 Ynoi-编程知识

浅谈操作分块：从 Div.3 F 到 Ynoi

news/2025/2/12 11:37:08/文章来源:https://www.cnblogs.com/lemonniforever/p/18706282

前言

分块是一种常见的处理信息的思想。

序列分块通常以 \(\mathcal O(q\sqrt n)\) 左右的时间复杂度对询问进行处理。观察序列分块的本质，其实是控制无法快速统计的部分较少，以至于可以暴力统计，剩下的部分采取诸如提前维护好每个块的答案再合并的方式快速统计。

而在答案具有可合并性、修改和询问并不是复杂操作时，我们还可以考虑对操作进行分块，控制块的大小并结合暴力统计与快速统计，做到在同样 \(\mathcal O(q\sqrt n)\) 左右的时间复杂度解决一类包括单点修改与询问的题目。

这样的 trick 就叫操作分块（又名询问分块）。

本文配套题单：Link

正文

操作分块的主要的思想就是合并贡献。

操作分块的主要策略是这样的：在某一块开始处理前先得到每个询问在该块前的答案或信息，因此对于块内的询问可以快速得知该询问由块之前操作造成的贡献或答案，而对于块中直接进行 \(\mathcal O(B^2)\) 枚举，考虑每个询问之前的块中的操作对该询问的贡献，然后合并在一起（合并的方式可能是 \(\max-\min\) 或相加等）。

伪代码形式如下（极度不严谨并且中式英语）：

第 \(2\) 行获得了每个询问在该块前的答案或信息，第 \(5\) 行计算了块之前的操作对答案的贡献，第 \(7\sim 12\) 行计算了块内操作对询问的贡献，第 \(18\) 行将本块中操作的贡献合入“块之前操作造成的贡献”，计算下一块中的询问。

除了上面那种直接合并贡献的方式，为了得到某块前的全部答案信息，还可能需要对前面的所有操作扫一遍或者进行暴力重构，因此操作分块一般还适用于整体重构复杂度比较低的操作，比如单点修改和虚树（只对部分关键点操作）。

而对于询问，操作分块一般用于单点询问或全局询问，因为这两类询问比较容易计算贡献，并且复杂度通常较低。

举个例子，不能操作分块的一个经典问题是：在不将问题转化到 \(pre\)（上一次某个元素出现的位置）序列上进行区间数颜色加单点修改。如果不转化为 \(pre\)，因为操作同时的颜色数不好合并，我们只能通过类似莫队的维护桶的方式做到这一点，然而很明显虽然我们做到了可以轻易计算并合并某次修改的贡献（用莫队的方法在桶上加减），但我们无法在可接受的时间内得到块之前每一个想询问的区间的桶，因此不能操作分块。

下面以几道题目为例，介绍操作分块的一些经典应用与配置。操作分块主要还是一种思想，只有结合题才能更深刻地理解，~~所以你就说我是不是差不多写了一整篇的题解吧~~。

CF342E Xenia and Tree：多源 BFS

本题正解是动态点分治，但注意到只对树上单点进行操作并且操作简单，不妨考虑操作分块。

首先我们考虑如何在块中 \(\mathcal O(B^2)\) 枚举时快速计算一个操作对一个询问的贡献，很明显是直接计算询问点与变红点在树上的距离一路取 \(\min\)。

然后考虑在本块之前就已经是红色的点，怎么去计算他们的贡献。于是我们不得不思考：如何得到块前的全部答案信息？如何在本块处理结束后将本块操作的贡献加入全部答案信息？

考虑维护一个 \(dis\) 数组表示每个点到本块前所有已经变红的点的最小距离，这样可以 \(\mathcal O(1)\) 地得到每个询问在块前的答案信息。想要处理新变红的点对 \(dis\) 的贡献，直接在块结束后将所有操作的红点放进 queue，对这些点跑一遍多源 BFS 并更新 \(dis\) 即可。

核心代码如下：

fr1(i,1,q){cin>>query[i].fi>>query[i].se;if(i%B==0||i==q){//新块fr1(j,lst,i){if(query[j].fi!=2){continue;}//先处理询问ans[j]=minn[query[j].se];//获取询问点在块之前与最近的红点的距离fr1(k,lst,j-1){//计算询问之前的块内操作对询问的贡献if(query[k].fi==1){ans[j]=minn[query[j].se]=min(minn[query[j].se],dis(query[j].se,query[k].se));}}}fr1(j,lst,i){if(query[j].fi==2){cout<<ans[j]<<endl;}}fr1(j,lst,i){if(query[j].fi==1){minn[query[j].se]=0;qq.push(query[j].se);}}bfs();//用多源BFS在可接受的时间内将本块的操作的贡献算入minn数组，保证下一块的minn数组符合其定义lst=i+1;//将块头改为下一块块头}
}

取 \(B=\sqrt n\)，于是我们成功以 \(\mathcal O(q\sqrt n+n\sqrt n)\) 的时间复杂度解决了问题。

因为多源 BFS 是一种常见的在 \(\mathcal O(n)\) 时间复杂度内求出每一个点到若干关键点最小距离的算法，所以使用多源 BFS 将本块贡献合并或是重构贡献效率很高。这个 trick 可以用于某些操作点上的信息，查询最小距离的题目。

一道类似的题目：CF1790F Timofey and Black-White Tree

CF925E May Holidays：虚树

本题在 CF 上的 std 采用的就是操作分块做法，因此本题也常被作为操作分块的模板题。感谢这篇题解在写作时的帮助。

首先考虑转化题意，限制本质上等价于黑点总数减去 \(t_i\) 后大于 \(0\)。因此先给每个节点 \(i\) 一个权值 \(-t_i\)，对于点 \(i\) 白变黑即为 \(i\to 1\) 的链上每个点的权值都 \(-1\)，反之即为 \(+1\)，然后对节点 \(i\) 反色，询问有多少个白点的权值 \(>0\)。

注意到修改单个节点，查询全局，考虑操作分块。

先考虑如何解决块内操作对询问的贡献。对于到根的链 \(\pm 1\)，如果暴力操作原树肯定不行，所以我们考虑上虚树，把所有要修改的节点全部设置成关键点建立虚树。因为这样做之后虚树上的节点数量是 \(B\) 级别的，我进行暴力操作的复杂度就是 \(\mathcal O(B)\)。

不会虚树可以移步这里。

然后你考虑如何在虚树上暴力操作却可以达到原树上操作的效果，可以尝试下放节点，使得虚树上一个节点 \(u\) 管理其在原树上从它到其虚树父亲这条链上的所有点（不含虚树父亲）。根据虚树性质，这样一定可以做到每一个虚树上的点都管理从它开始在原树上向上的一条链，当我们在虚树上从一个虚树点暴力 \(\mathcal O(B)\) 向上跳一直跳到根时（很明显虚树根也是原树根），如果我们能较快地维护路上经过的虚树点上管理的节点的信息，那我们只需要在每个节点上都操作这些信息，就等于链的操作。

因为询问是询问权值 \(>0\) 的点的个数，所以在虚树节点上我只需要维护其管理的点的权值，一个自然地想法是把这些权值拿下来排序，然后你可以发现，当我做链 \(\pm 1\) 时，其实就是这些权值全部 \(\pm 1\)。那么如果之前存在权值为 \(0\) 的点，我再做 \(+1\) 那么它们将计入答案，而如果之前存在权值为 \(1\) 的点，我再做 \(-1\) 那么它们将不再计入答案。

于是不妨考虑不再实时维护所有数的权值，而维护这个分界点与目前该点上的增减量 \(add\)。给每一个虚点维护一个指针，表示在排序后的原权值中，在指针前面的数加上 \(add\) 都 \(>0\)。那么当我们把相同的权值合在一起并记录出现次数的时候，每一次指针移动的偏移量都是 \(\mathcal O(1)\) 的，而指针每次移动就往答案中加入或减掉新计入或离开的权值的出现次数，就可以维护答案了。

于是现在我们就做到了操作分块中快速计算块内操作对询问贡献的步骤，再观察刚刚的过程，可以发现每块的操作结束后我都可以暴力走一遍原树，利用记录的 \(add\) 修改所有点的权值，这样到下一块开始处理时，树上所有点的权值都刚好是块之前的最新的权值，只需要在虚树建好之后立即按照定义初始化一下指针，就可以得到在块之前的操作对答案的初始贡献。

用图总结一下我们到现在的过程：

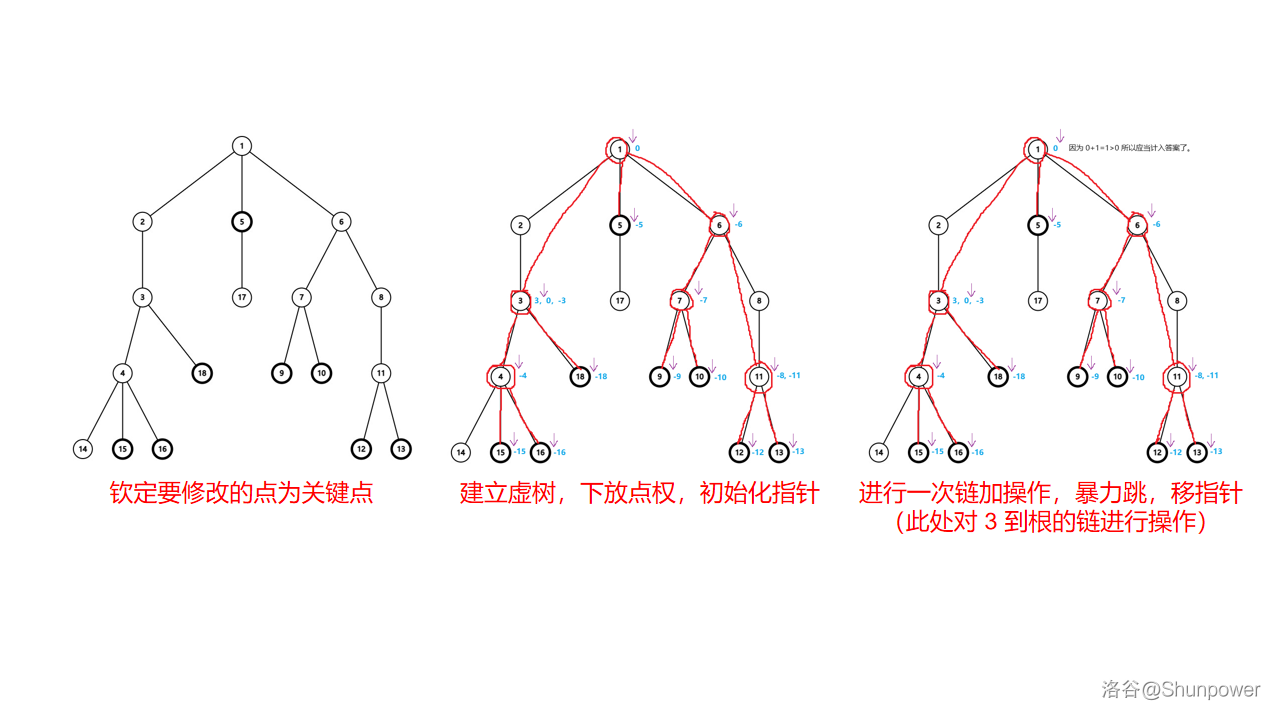
在上图中，如果再对 \(3\) 到根的链做 \(3\) 次链加操作，那么 \(3\) 号点的指针将再次后移一位，但根节点 \(1\) 的指针将不再后移。实现指针移动时，可以通过我们前面说的增减量 \(add\) 加上指针前面或后面的数的值，判断指针是否需要前后移动，因为 \(add\) 每次只会增加或减少 \(1\)，所以指针每次最多只会移动一个数的位置（例如从 \(3,4,4,4,4,5\) 的 \(4\) 后面移到 \(4\) 前面），但是我们又把相同的数合在了一起，所以指针每次最多只会移动恰好一位，也就 \(\mathcal O(1)\) 了。

但是我们还没有做完这道题。还有一个给点反色的操作我们没有实现。可以发现，如果一个点由黑变白，那么我们就要删去这个点的贡献，我们不妨在它管理的所有点的权值序列中找到它自己的权值，然后把这个权值删去（直接扣掉一次出现次数）。注意如果这个权值的位置在指针前面，则还需要给答案扣掉 \(1\)。如果这个点由黑变白，那么就要把这个点的权值加回去，如果加在指针前面，则要给答案增加 \(1\)。

所以实际上，我们的虚树节点要管理的权值序列，是它所管理的点中的白点构成的权值序列，黑点我们是不用关心的。因为除了这个点本身，是不可能在它管理的其他节点中出现黑变白的情况的，否则那个点也会成为一个虚树节点。

talk is cheap，这里有一份注释过的正解代码。

本题中，每块的复杂度为 \(\mathcal O(B^2+n\log n)\)，因为需要排序，因为 \(B<n\) 所以二分的 \(\mathcal O(B\log n)\) 我们不计入复杂度。总的复杂度即为 \(\mathcal O(qB+\frac{qn\log n}{B})\)，取 \(B=\sqrt{n\log n}\) 即可做到 \(\mathcal O(q\sqrt{n log n})\)。

将操作分块中的操作点设置为关键点，建立虚树，因为虚树大小是 \(\mathcal O(B)\) 的，所以将原树操作转为在虚树上的暴力操作可以带来可接受的复杂度（即 \(\mathcal O(B^2)\)），而在维护虚树上的暴力操作时，为了保证不忽略原树节点的信息，通常采用下放节点的方式在虚树上进行管理，这样效率和正确性都得到了保证。这种 trick 适用于在树上操作关键点，查询全局信息的题目。

CF1866F Freak Joker Process：拆贡献

题目大意：
有 \(n\) 名选手组成了一个 OI 队。第 \(i\) 名选手的思维能力是 \(A_i\)，他的思维能力排名 \(\text{RankA}_i\) 被表示为 \(A_j>A_i\) 的 \(j\) 的个数 \(+1\)；第 \(i\) 名选手的代码能力是 \(B_i\)，同理定义了他的代码能力排名 \(\text{RankB}_i\)。第 \(i\) 名选手的综合实力为 \(\text{RankA}_i+\text{RankB}_i\)，综合实力排名为 \(\text{RankA}_j+\text{RankB}_j<\text{RankA}_i+\text{RankB}_i\) 的 \(j\) 的个数 \(+1\)。你需要维护将某位选手的思维或代码能力 \(\pm 1\)，以及查询某位选手的综合实力排名两种操作。

官方题解在这里，一上来就是~~一坨公式糊我一脸~~，我理解了一晚上才大概搞明白。

这道题看上去是一道困难的数据结构题目，注意到单点修改，查询全局排名，考虑操作分块。为了防止变量名冲突，在这一部分，我们把块长定义为 \(l\)。

我们仍然先考虑块内操作对询问的影响。发现 \(\text{RankA},\text{RankB}\) 想直接全部维护比较麻烦，因为相等的数可能很多，每次修改需要操作的数不是 \(\mathcal O(1)\) 的。不妨设两个数组 \(a,b\)，其中 \(a_x\) 表示大于 \(x\) 的 \(A\) 值有多少个，那么 \(\text{RankA}_i=a_{A_i}+1,\text{RankB}_i=b_{B_i}+1\)，很明显 \(a,b\) 我们都是可以在开头 \(\mathcal O(V)\) 求出，后面 \(\mathcal O(1)\) 动态维护的，每当我们改变对 \(A,B\) 中的一个值 \(v\) 做 \(\pm 1\) 的操作，\(a,b\) 中都只有 \(v\) 的那一项会发生变化。因为维护了 \(a,b\) 数组，所以 \(\text{RankA},\text{RankB}\) 我们也可以在需要的时候 \(\mathcal O(1)\) 查到了。

很自然可以想到计算询问的选手 \(i\) 的 \(\text{RankA}_i+\text{RankB}_i\)，只需要查询有多少个 \(\text{RankA}_j+\text{RankB}_j\) 的 \(j\) 比它小就好了。我们令询问选手 \(i\) 的 \(\text{RankA}_i+\text{RankB}_i\) 为 \(w\)。

首先根据操作分块的思维方式，我们可以想到计算要改变 \(A,B\) 的选手对答案的贡献。很明显这样的选手最多只有 \(l\) 个，所以我们直接暴力维护和统计这 \(l\) 个选手的 \(\text{RankA}+\text{RankB}\) 就行了，这是 \(\mathcal O(l^2)\) 的。

这样是不是就做完了呢？当然不是。比如 @StayAlone \(7\) 岁的时候某一次模拟赛~~场切黑题~~，他的思维能力从普及三等上升到了（国家）队爷，但是 @Shunpower 还是只会做提高组的题，那么虽然 @Shunpower 没有被操作，但是他的 \(\text{RankA}\) 还是降低了。这种排名被波及到导致的综合排名变化我们也需要考虑。

于是我们再考虑一下怎么维护这些像 Shunpower 一样的选手。首先可以发现，这样的选手一定是在 \(a,b\) 中发生变化的项的能力值对应的那些选手，因为最多只有 \(l\) 名选手被操作，所以发生变化的项也只有 \(l\) 项。根据官方题解，我们把这样的项的值称作特殊值。那么我们就可以在询问时将没有被操作的选手分为三类，一种是某一项能力是特殊值（即其中一项的排名被波及到），一种是两项能力都是特殊值（即排名都被波及到），最后一种是啥也不是的选手，既没有被波及，也没有被操作。

首先很明显所有啥也不是选手的 \(\text{RankA}+\text{RankB}\) 永远不会变化，我们把这些算出来然后在块头做一次 \(\mathcal O(V)\) 前缀和就可以得到有多少啥也不是选手的 \(\text{RankA}+\text{RankB}<w\)。

先考虑某一项能力是特殊值的选手。假设他们的能力 \(A\) 是特殊值，那么这种选手的 \(\text{RankB}\) 一定不会受到波及，所以可以直接每块 \(\mathcal O(n)\) 算出所有选手的 \(\text{RankB}\)，然后排序放进一个数组，然后对于每个询问，当时我们一定能算出 \(l\) 个特殊值 \(A_i\) 的最新排名 \(\text{RankA}_i\)，枚举 \(l\) 个特殊值得到 \(\text{RankA}_i\)，二分那个数组有多少个 \(\text{RankB}_j<w-\text{RankA}_i\)。对于 \(B_i\) 是特殊值的选手同理。这样每个询问一共要在 \(n\) 长度的数组中先排序再二分 \(l\) 个值，单块总复杂度为 \(\mathcal O(l^2\log n)\)。

然后考虑最后一种选手，这是最困难的部分。注意到每一次变化，对于这些选手都只有 \(l\) 个不同的 \(\text{RankA}+\text{RankB}\) 发生了变化（因为两边都只有 \(l\) 个特殊值，而每次又只有其中一项变化，所以算上另一项就只有 \(l\) 个发生了变化），所以我们可以维护一个这种选手的 \(\text{RankA}+\text{RankB}\) 数组，下标为 \(i\) 的项表示 \(\text{RankA}+\text{RankB}<i\) 的这种选手数量。不妨先获取所有特殊值，然后开一个 \(cnt_{i,j}\) 数组表示 \(A\) 能力是 \(A\) 中第 \(i\) 个特殊值，\(B\) 能力是 \(B\) 中第 \(j\) 个特殊值的这样的选手的数量，然后对于每次变化，我们很明显可以知道排名变化的特殊值是哪一个，所以枚举另外一边是哪个特殊值，又因为每次排名变化只有最多 \(1\) 位，所以，就能用单块总共 \(\mathcal O(l^2)\) 的时间计算这种选手的贡献。

下一块需要的变量只有在本块 \(\pm 1\) 操作之后新的每一位选手的能力值，这个很明显可以直接做一遍所有操作得到。

此处 \(n,V\) 同阶，单块复杂度即为 \(\mathcal O(n+l^2\log n)\)，取 \(l=\sqrt q\) 得到总复杂度为 \(\mathcal O((n+q)\sqrt q\log n)\)。

这道题也引出了操作分块中拆贡献的思想。在这道题里面我们经过一通对选手的情况的讨论，干了拆贡献的工作，再在操作分块中算贡献，最后合并拆出去的贡献，~~然后搞得麻烦得要死~~才解决了这道题。

因为这玩意太难写了，代码暂时先咕着有空再更。CF 上的提交记录也没什么好东西，除了 \(\color{black}\textsf{j}\color{red}\textsf{iangly}\) 的神仙在线做法剩下的基本全是指令集，唯一一篇洛谷题解是指令集，~~好像最优解都是指令集~~。这份代码可读性还算比较好，在我补上这里的代码之前可以先将就用着。

小结

上面我们讲的操作分块主要分为以下步骤：

获取一些初始信息
计算块中的操作对答案的贡献（一般是枚举询问和前面的操作 \(\mathcal O(B^2)\) 暴力）
计算块前的操作对答案的贡献（可能是一种全局数据结构，也可能是扫一遍前面所有的操作或者信息）
重构或者维护信息

在计算贡献的途中需要把贡献合并。当然，也有可能是把答案拆成子贡献，在操作分块里合并子贡献，再把子贡献合并成总贡献。

如何看出题目需要采用操作分块呢？除了有一些做过就知道的 trick 以外，还有一种想法是得到两种暴力并且考虑结合他们。例如 CF342E Xenia and Tree，你可以想到一种针对询问的 \(\mathcal O(n\log n)\)（可以使用 \(\mathcal O(1)\) LCA 做到 \(\mathcal O(n)\)）枚举得到一个询问答案的暴力，也可以想到一种针对操作用 \(\mathcal O(n)\) 更新所有询问答案的 BFS 暴力，这两种暴力各有优劣，一个对于询问，一个对于操作，可以想到用操作分块结合。

还可以从操作分块的本质入手。操作分块的本质就是把块内转成一个可以直接上 \(\mathcal O(nq)\) 暴力的问题，块外相当于做一个“所有操作都在询问之前，可以随便离线”的弱化问题。同样是对于 CF342E Xenia and Tree，你发现假设所有操作都在询问之前，只需要把所有黑点都拿出来多源 BFS 跑一遍所有点的答案就行了，结合一下纯暴力和这个弱化的做法就能用操作分块解决问题。

~~这里应当出现 lxl~~：P7711 [Ynoi2077] 3dmq。这个操作和询问很容易转成点加和三维数点，能够发现贡献是好拆的，并且这两种操作都比较全局因此可以考虑操作分块。因为实在太复杂了，还没有研究具体做法，如果以后有时间会在这里加上这道题的内容的。把题挂在这里欢迎读者研究。

一道比较容易的练习题：[ABC256F] Cumulative Cumulative Cumulative Sum，单点修改，查询三次前缀和的单项。题解区可以找到我的操作分块题解。

另一道比较容易的练习题：GYM102452I Incoming Asteroids，警报器类问题可以尝试用操作分块离线解决。我们只需分块后，在每块块末检查警报器，将在这块内报警的警报器再在块内寻找一下报警的点就可以了。当然也可以使用折半警报器或 zak 警报器用 polylog 解决。读者可以继续尝试用类似操作分块的方式解决 QOJ8035. Call Me Call Me。

一道稍微有点难的练习题：CF1254D Tree Queries，其实也不是很难吧……认真想一下很容易可以通过操作分块得到一个 \(\mathcal O(B^2+\frac{q}{B}n\log n)\) 的基于 BIT 重构和长剖求 \(k\) 级祖先的做法（这篇题解可能对你有帮助），\(q,n\) 同阶于是取 \(B=\sqrt {n\log n}\) 就能得到一个 \(\mathcal O(n\sqrt{n \log n})\) 的算法。当然其实不写长剖直接倍增也能过，只是特别卡，一通卡常猛如虎才能以 \(4.5\) 秒左右的时间通过。经过卡常后比较抽象的代码和卡常之前比较形象的代码都提供给大家。

[APIO2019] 桥梁：贡献不删除

这是一种在写法和外观上和上面所有各种操作分块都有所不同的操作分块，~~果然 APIO 是 trick 制造机吗~~。我们上面所做的事情其实都是预先算好每个询问的块前贡献，在询问的时候直接拿出块前贡献就完事了。但是有的操作分块，询问可能不只是某个单点，可能还有附加的权值等等，这种情况我们没办法直接全部预先处理出来块前的贡献，也不能每个询问都扫一遍前面的所有操作。有没有什么办法可以干掉这个附加的权值呢？

我们考虑“每个询问都扫一遍前面的所有操作”这个方向。每个询问都扫一遍是不是有点太浪费了？因为有了权值，所以有一些操作可能对某个询问是无效的！~~不然权值的意义是什么~~

（\(\text{upd:}\) 当然这里可能有点以偏概全。但是在这种操作分块中，权值必须能够使得一些操作对某个询问无效，否则无法使用这种操作分块，因为重算块前贡献被定死在了每次 \(\mathcal O(n)\)，复杂度等于甚至大于暴力。）

然而即便是这样，如果只扫那些对这个询问有影响的操作，在这道题里面渐进复杂度完全没有任何变化。权值能够使一些操作对询问无效，并不代表总是可以使一些操作对询问无效。

我们再往下想，我们已经只想考虑那些只对这个询问有影响的操作了，能不能快速得到这些操作的贡献呢？还是说，我可不可以维护它们，让我在计算这个询问的时候这些操作正在某种数据结构中，我可以直接考虑呢？

前者比较难办，我们考虑后者。然后你就发现，假设我确实存在这样一种数据结构，那我在算完这个询问之后，我要清空掉整个数据结构，然后把影响下一个询问的操作的贡献又加入这个数据结构。你发现这个清空数据结构又加回去的操作也太憨了，我可以把这次的给留下来，这样我下次只有加，不用撤销或者清空了。放宽一点，我允许一些撤销和清空，但是只要我能保证每个操作的贡献都加入数据结构常数次，或者次数比较少，我的复杂度就是对的啊！

那怎么减少撤销和清空的次数呢？我只要想办法尽量让影响可以被继承下去就好了。举个例子，如果某个操作同时对询问 \(q_1,q_2\) 做贡献，但不对 \(q_3\) 做贡献，那我为了减少撤销的量，我给询问排个序，搞成 \(q_3,q_1,q_2\)，这样我的影响加入之后就不会再被撤销了。换句话说，其实就是对于每一个操作，存在一个单调性：后算的询问总是受这个操作影响，先算的询问总不受这个操作影响。

当然也可以反过来，一开始所有操作的贡献都在数据结构里，我想减少加入的量，让每个操作撤销一次或者很少的次数，让先算的询问总是受这个操作影响，后算的询问总是不受这个操作影响也是可以的。

需要注意，这种操作分块不一定必须只撤销或者加入一次，\(\log\) 级别之类比较少的次数都是可以的。

接下来回到这道题，我们发现假设存在两个询问的车的重量分别是 \(w_1,w_2(w_1>w_2)\)，那么 \(w_2\) 车可以通过的桥梁一定是严格包含 \(w_1\) 车可以通过的桥梁的。于是操作就可以继承了！我可以先将所有询问的车的重量从大到小排序，这样做之后，如果一座桥梁前面的车可以通过，后面的车也一定可以通过，一座桥在加入贡献之后，一定不会有问题了。

当然前提是要先移除那些在块内被修改重量限制的桥。

然而还有一个问题，虽然这样我避免了一座桥的贡献被撤销，但我每次处理询问的时候，还有一些桥梁是要被加入的，怎么找到这些要加入贡献的桥呢？

很容易想到，还可以把桥按照块前最终的重量限制也从大到小排个序。并维护一个指针表示目前加入的最后一座桥。当我切换下一个询问时，我直接后移指针，将重量限制大于等于询问车重量的桥加入贡献，直到下一座桥的重量限制小了或者没有桥了。这个过程和归并排序其实是比较像的。

在这道题里，答案是询问的点在仅经过重量限制大于等于车重量的桥的情况下，能够到达的点的数量，转换一下就是在图中只有重量限制大于等于车重量的桥的情况下，询问点所在连通块的大小。这个直接并查集就能轻易做到加入一座桥，并且不方便撤销任意一座桥，这也正好对应了我们这类询问分块“不撤销、少撤销”的特点（所以其实从并查集入手来想也能想到我们这种不撤销类型的操作分块，因为很难维护图的连通性）。

而剩下的在块内有修改的桥是好做的。对于每个询问，你需要考虑在它前面被修改的桥的最终重量限制，再往前是怎么改的根本不重要，直接把满足条件的桥加入并查集就好了。还有一些桥块内有修改，但不在询问前面，我们还没有把它们算进贡献当中，需要得到这些桥在块之前的最终重量限制然后再把满足条件的桥加入并查集。

然而还有一点小问题，因为块内操作的顺序被打乱了，所以块内操作加的桥不具有继承性，必须要撤销掉。不过我们加这些桥是连续的一段过程，并且这些桥的数量是块长的，我们直接用可撤销并查集暴力撤销掉就行了。你也可以理解成，我们通过破坏块内操作的继承性换来了块前操作的继承性，以保证复杂度的正确。

注意可撤销并查集不能路径压缩，只能启发式合并所以并查集复杂度是 \(\mathcal O(n\log n)\) 的。总复杂度即为 \(\mathcal O(\frac{q}{B}(m\log m+B^2\log n))\)，也就是 \(\mathcal O(\frac{qm\log m}{B}+qB\log n)\)，考虑到 \(m\) 总是大于 \(n\)，取 \(B=\sqrt m\) 时复杂度可以做到 \(\mathcal O(q\sqrt m\log m)\)，应该是最优复杂度。因为 \(q,m\) 同阶，我一开始取了 \(B=\sqrt q\) 是能过的，~~但是 LOJ 上总时间要一百多秒并且会出现有一个点差六毫秒 TLE 的情况，而且洛谷过不了，当然不影响我们在 LOJ 上用神机加持碾题~~。

此外经过测试，使用非常憨的主席树大力可持久化并查集去撤销块内桥的贡献会被卡常，~~在洛谷上只能获得八分的好成绩~~，我尽力调整块长使得主席树的常数得到平衡，然而事实是最快也只能做到（这是 \(n\approx 3\times 10^4\) 的数据）：

我在本地偶尔能做到 \(5\) 秒左右，当然还是不可能通过这道题，这里是一发主席树的提交记录，可以看到~~在 LOJ 的超算上~~还是 TLE 得很死的。使用常数比较小的可撤销并查集再卡卡常就能过啦（用可撤销并查集跑上面的数据只需要 \(0.5\) 秒）。

我的最终代码常数比较大，但是写得应该还是很好理解的。这份代码选择了前人得出的较快的块长 \(1000\)，并且成功在洛谷的评测机上通过了。

开头已经提到，这种操作分块与我们之前说的几乎都不太相像。它的询问确实符合一般操作分块的“块前贡献+块内贡献”的模式，但在算块前贡献的时候遇到了障碍，我们需要找到块前贡献的特殊性。比如这题就需要我们注意到贡献边与询问权值必须存在的偏序关系，然后自然地想到两边排序进行一个类似双指针的操作，使得一条边的贡献不会被多次删除、插入，也就保证了并查集的正确性与复杂度。

大多数操作分块的难点其实都在于怎么复杂度正确的计算块前贡献。把这些贡献插入全局数据结构，再对询问依次查询是最常见的解决办法，但是考虑本质就会发现，导致任何复杂度接近 \(\mathcal O(n)\) 的处理方法都是可能出现的（尤其是因为操作分块的离线性导致可扩展性非常强）。比如甚至可以做带修三维偏序，每一块统计块前贡献时进行 cdq 分治，~~没关系，它当然被 cdq 套 cdq 的四维偏序爆踩了~~。

所以做操作分块题还是不要被 trick 束缚，操作分块并不是很强劲的算法，甚至可能也无法带来很强的性质，它本质上始终只是弱化了问题，新的问题可能仍然很困难，也仍然具有多样性。