[gym 102428] Fabricating Sculptures

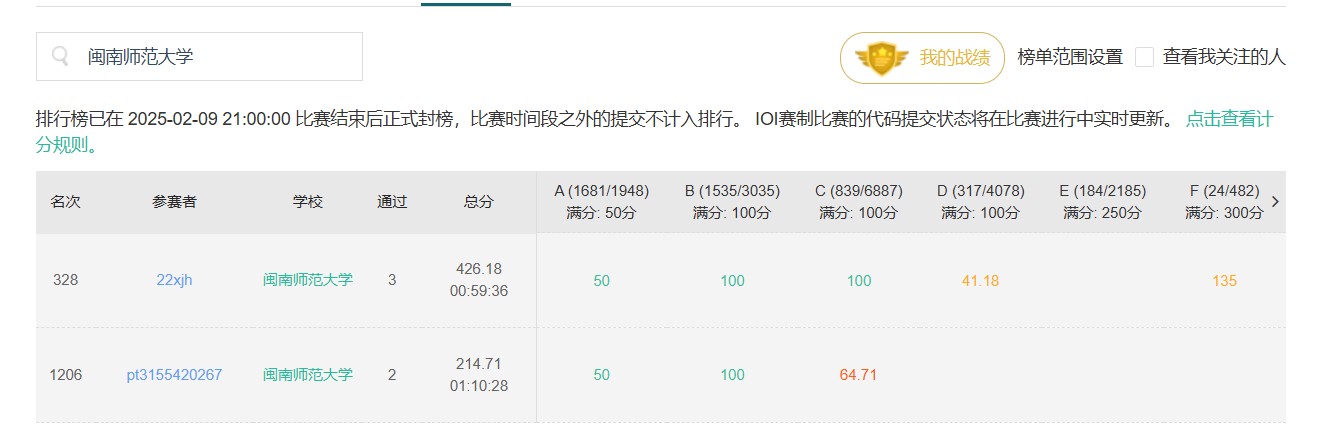
前言

现在补题是不是不太好

思路

转化题意

给定列数 \(S\) , 方块数 \(B\) , 求一种摆放方式, 使得每一列的方块数 \(a_i\) 满足 \(a_i \geq 1\) 且 \(a_i\) 呈非严格单峰

观察单峰函数的性质, 发现如果按行处理, 就是单调不增的
更一般的, 每一行放置的方块数非严格小于上一行放置的方块数且必须连续

那么计数 \(\rm{dp}\) 就简单了, 令 \(f_{i, j, k}\) 表示考虑到第 \(i\) 行 \((\)从上往下\()\) , 当前行放了多少列, 总共用了多少个方块
转移就是上一行的方案数, 每种情况在这一行的基础上往下增加 \(k\) 个方块

\[f_{i, j, k} \gets \sum_{l = 0}^{j - 1} f_{i - 1, j - l, k - j} \times (l + 1) \]

最后乘以 \(k + 1\) 表示可以在上一行的基础上滑动长度为 \(l + 1\) 的距离:

不难发现可以滚一维

进一步的, 你发现其时间复杂度为 \(\mathcal{O} (B^3S)\) , 需要优化

这样形式的柿子, 完全可以提前处理出 \(sum_{k - j}\) 表示 \(\displaystyle \sum\limits_{l = 0}^{j - 1} f_{i - 1, j - l, k - j} \times (l + 1)\)
不难发现每次复杂度变为 \(\mathcal{O} (b^2S)\) , 更新 \(sum\) 只是 \(\mathcal{O} (1)\) 的事

总结

转化成要求非严格单峰非常聪明, 因此才想到按层处理而非按列处理
注意思路走不通时, 考虑换一个方向

这道题特别的地方在于, 虽然每个 \(f\) 在更新时要乘以 \(l + 1\) , 但是事实上每个 \(f\) 仅仅对应唯一的 \(k - j\) , 对应更新寄了