重做 CF906E Reverses

• 不是，JJ 怎么退役了，悲。
• 嗯，先有

\[dp_{r}=\min_{l=1}^r[s(l,r)\text{是回文串，且长度不为 2}]dp_{l-1}+1 \]

• 总复杂度就 \(n^2\)，考虑优化
• 然后有引理说，一个字符串的所有 border 构成 \(\log n\) 个等差数列
• 我们考虑什么样的点能够转移到 \(dp_i\)

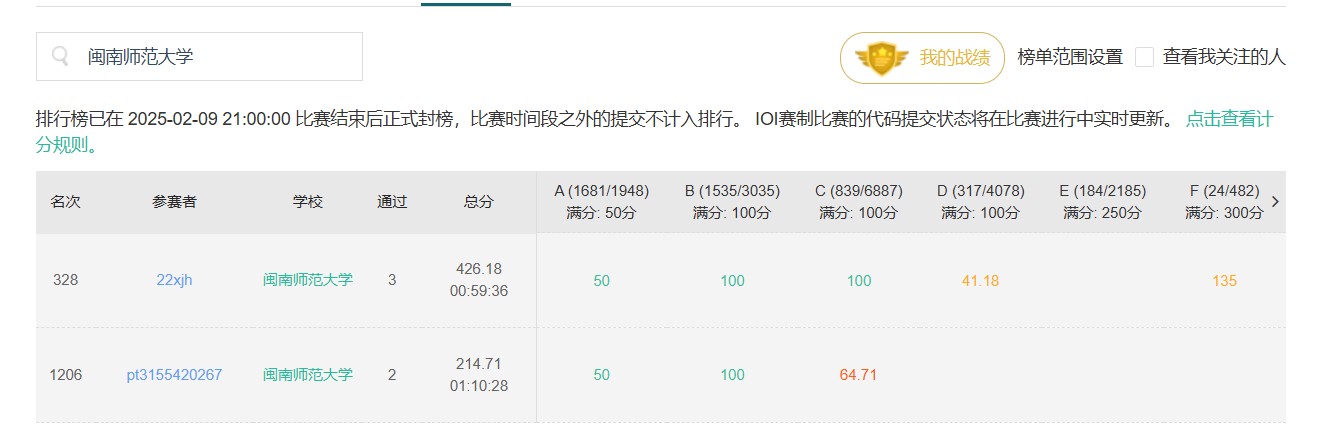
• 尝试借助 \(log\) 段，成段转移，具体的，正如上图，右侧所示，我们把每一段的 \(dp\) 值的最大值存到蓝色点，即段的最长节点，嗯，对，紫色存到蓝色里。至于为什么是这样，之后解释。
• 由于回文自动机只记录回文串，并不记录回文串的位置，所以我们考虑 log 段上的一段，在加了若干个字符的变化，如图。

• 当某一时刻，我们加了一段绿色的段，而在回文自动机上有大量重复的节点。首先我们有 红色括号里的等于紫色括号里的。所以我们粉色框所代表的上一个转移点，与紫色括号的转移点是相同的。
• 紫色线条表示的是两个段字符串相等（不是 好像没啥用）
• 之后注意，我们把什么样的算作一段，蓝色块开头，带着一堆紫色块。
• 所以与之前的转移点一一对应，少的不是最底下的蓝色块（我卡在这半天）。而是上面的紫色块。蓝色算作下一段的开头。所以我们补上的是 \(i-diff-slink\) 的位置

• 之后，感性理解一件事情，log 段中，每一段的开头在原串中开头在回文自动机中存的值一定不是位置 \(x\) 而是紧接着的前一个位置 \(y\)
• 而次小串 \(x'\) 上一次出现的位置是 \(x''\) 而不是 \(y'\)。所以我们取之前的 \(x''\) 在回文自动机里的值来更新当前位置 \(x\) 是没有问题的，因为必定是紧接着的前一个。也是为什么把总贡献存到最大位置的原因，因为可以从小逐步更新，保证继承的一定是前一段。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 500050;
char s1[N], s2[N], s[N << 1];
struct Node { int trans[26], fail, len, diff, slink; }tr[N << 1]; int idx = 1;
int Fail(int x, int i)
{while (s[i] != s[i - tr[x].len - 1])x = tr[x].fail;return x;
}
int f[N << 1], g[N << 1], ans[N << 1];
void insert(int i)
{static int edp = 1;int pos = Fail(edp, i);if (!tr[pos].trans[s[i] - 'a']){idx++;tr[idx].fail = tr[Fail(tr[pos].fail, i)].trans[s[i] - 'a'];tr[pos].trans[s[i] - 'a'] = idx;tr[idx].len = tr[pos].len + 2;tr[idx].diff = tr[idx].len - tr[tr[idx].fail].len;tr[idx].slink = (tr[idx].diff ^ tr[tr[idx].fail].diff) ? tr[idx].fail : tr[tr[idx].fail].slink;//printf("New: %d %d %d %d\n", tr[idx].fail, tr[idx].len, tr[idx].diff, tr[idx].slink);}edp = tr[pos].trans[s[i] - 'a'];if (i % 2 == 0 && s[i] == s[i - 1] && f[i] > f[i - 2])f[i] = f[i - 2], ans[i] = i - 2;for (int k = edp; k; k = tr[k].slink){g[k] = i - tr[tr[k].slink].len - tr[k].diff;if (tr[tr[k].fail].diff == tr[k].diff && f[g[k]] > f[g[tr[k].fail]])g[k] = g[tr[k].fail];if (i % 2 == 0 && f[g[k]] + 1 < f[i]) f[i] = f[g[k]] + 1, ans[i] = g[k];}
}
int main()
{memset(f, 0x3f, sizeof f);tr[0].fail = 1; tr[1].len = -1;scanf("%s%s", s1 + 1, s2 + 1);int n = strlen(s1 + 1);for (int i = 1; i <= n; i++)s[(i << 1) - 1] = s1[i], s[i << 1] = s2[i];n = n << 1; s[n + 1] = '\0';f[0] = 0;for (int i = 1; i <= n; i++)insert(i);if (f[n] > 1e9)puts("-1");else{printf("%d\n", f[n]);for (int i = n; i >= 1; i = ans[i])if (i - ans[i] != 2)printf("%d %d\n", ans[i] / 2 + 1, i / 2);}return 0;
}