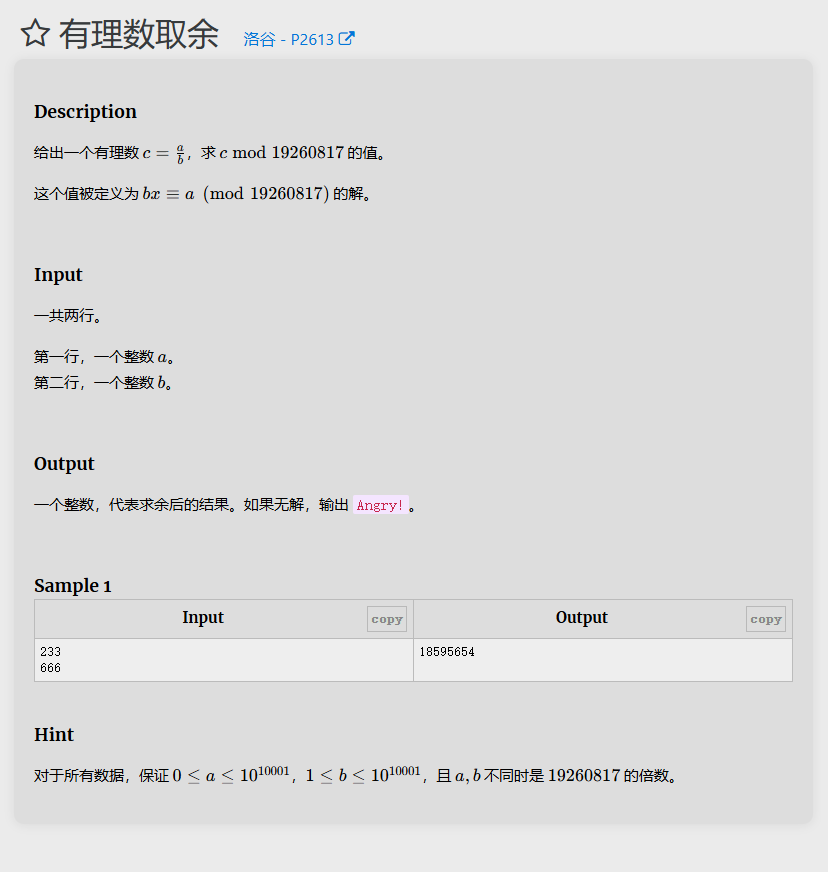
题目1
代码
#include<bits/stdc++.h>#define endl '\n'using namespace std;#define int long longint power(int a,int b,int p)
{int tar=1;while(b){if(b&1)tar=(tar*a)%p;a=(1ll*a*a)%p;b>>=1;}return tar;
}int read(int p)
{int tar=0;string s;cin>>s;for(int i=0; i<s.size(); i++)tar=(tar*10+s[i]-'0')%p;return tar;
}const int p=19260817;
int a,b;
signed main()
{// freopen("test.in","r",stdin);// freopen("test.out","w",stdout);/* Code */a=read(p);b=read(p);if(b==0)cout<<"Angry!"<<endl;elsecout<<(a*power(b,p-2,p))%p<<endl;// fclose(stdin);// fclose(stdout);return 0;
}解题思路
该代码实现了一个模意义下的快速幂运算,以及一个模意义下的整数读取函数。
power 函数使用了快速幂算法,通过不断平方和取模来高效地计算 a 的 b 次幂对 p 取模的结果。
read 函数用于读取一个字符串表示的整数,并将其对 p 取模。
在 main 函数中,首先读取两个整数 a 和 b,然后判断 b 是否为 0,如果是,则输出 "Angry!",否则计算 a 乘以 b 的逆元(即 b 模 p 的乘法逆元),并输出结果。
题目2

代码
#include<cstdio>
int t,l,r;
int main(){scanf("%d",&t);while(t--){scanf("%d%d",&l,&r);if(r==1&&l==1)puts("1");else printf("%d\n",r-l);}
}
解题思路
该代码的目的是计算从 l 到 r 范围内所有整数的差的绝对值,除了 l 和 r 都为 1 的情况。
在 main 函数中,首先读取整数 t,表示测试用例的数量。然后使用一个循环来处理每个测试用例。
对于每个测试用例,读取 l 和 r,并检查是否 l 和 r 都为 1。如果是,则输出 1,否则输出 r-l。
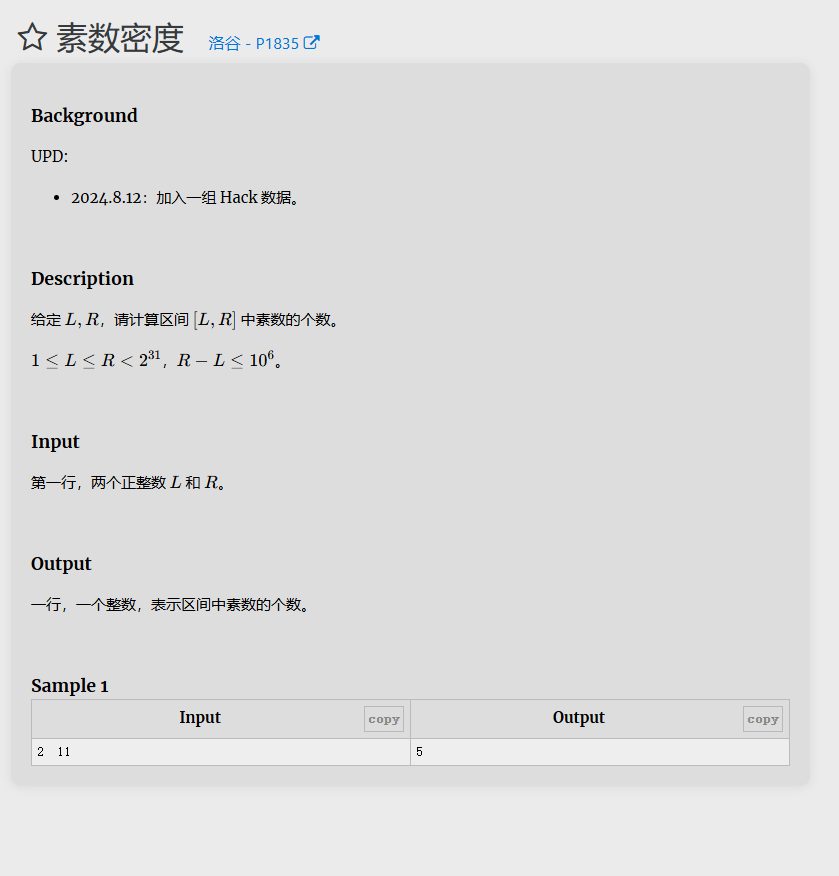
题目3
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 10;int primes[N];//存储所有素数
bool vis[N],a[N];//vis存储i是否被筛掉
//数组a记录偏移后的数据是不是合数,1:合数;0:质数。a[i]表示l+i是不是合数, 有一个偏移量l
ll l,r;
int cnt; void get_primes()
{cnt = 0;for(int i = 2; i <= 50000; i++){if(!vis[i]) primes[cnt++] = i;for(int j = 0; primes[j] <= 50000 / i; j++){vis[primes[j] * i] = true;if(i % primes[j] == 0) break;}}
}ll read()
{ll s=0,f=1;char ch=getchar();while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}while (ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}return s*f;
}int main() {l = read(),r = read();l = l == 1 ? 2 : l;get_primes();for(int i = 0; i < cnt; i++){ll st = max(2ll,(l-1) / primes[i] + 1) * primes[i];for(ll j = st; j <= r; j += primes[i]) a[j - l] = true;}//区间范围,因为我们无法完全映射所有的区间,只能采用类似于偏移的办法对某段区间整体偏移l进行描述。int ans = 0;for (ll i = l; i <= r; i++) if (!a[i - l])ans++;printf("%d", ans);return 0;
}
解题思路
该代码使用了埃拉托斯特尼筛法来找出给定区间 [l, r] 内的所有素数。
get_primes 函数初始化了一个素数数组 primes 和一个布尔数组 vis,用于标记每个数是否为素数。然后使用筛法找出所有素数。
在 main 函数中,首先读取 l 和 r,并确保 l 不为 1。然后调用 get_primes 函数来获取素数。
接着,使用另一个循环来标记区间 [l, r] 内的所有合数。对于每个素数 p,计算其在区间内的最小倍数,并将这些倍数标记为合数。
最后,遍历区间内的所有数,统计素数的数量并输出。
题目4

代码
#include<iostream>
using namespace std;
int x, y;
int main() {cin >> x >> y;if ((y%x) != 0) {cout << 0 << endl;}else {int q = y / x;int begin = 2;int ans = 0;while (q > 1) {if ((q%begin) == 0) {ans++;while ((q%begin) == 0) {q /= begin;}}begin++;}cout << (1 << ans) << endl;}return 0;
}解题思路
该代码的目的是找出一个数 x 的所有因子,并计算这些因子的幂集的大小。
在 main 函数中,首先读取 x 和 y,然后检查 y 是否能被 x 整除。如果不能,输出 0。
如果 y 能被 x 整除,计算 q = y / x,并初始化一个变量 begin 为 2。
使用一个循环来找出 q 的所有质因子。对于每个质因子,将其幂次加 1,并更新 ans。
最后,输出 2 的 ans 次幂,即因子幂集的大小。
题目5

代码
# include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+30;
int cnt[maxn], cnt2[maxn], a[maxn];
int main()
{int n, m;scanf("%d%d",&n,&m);for(int i=0; i<n; ++i){scanf("%d",&a[i]);if(a[i] <= m) ++cnt[a[i]];}for(int i=1; i<=m; ++i)for(int j=i; j<=m; j+=i)cnt2[j] += cnt[i];int ans = 0, id = 1;for(int i=1; i<=m; ++i)if(cnt2[i] > ans) ans = cnt2[i], id = i;printf("%d %d\n",id, ans);for(int i=0; i<n; ++i)if(id % a[i] == 0)printf("%d ",i+1);return 0;
}
解题思路
该代码的目的是找出一个数组中所有元素的最大公约数,并输出这个最大公约数以及它在数组中出现的次数。
在 main 函数中,首先读取 n 和 m,表示数组的大小和最大公约数的上限。
然后读取数组 a,并统计每个数出现的次数。
使用两个嵌套循环来计算每个数的倍数出现的次数,并更新最大公约数和出现次数。
最后,输出最大公约数和它在数组中出现的次数,并输出数组中所有能被最大公约数整除的元素的下标。
题目6

代码
#include<cstdio>
#include<algorithm>
using namespace std;
int mark[400001],a[100001];
int main(){int T,n,cntp,ans;for(register int i=2;i<=400000;++i) if(!mark[i]) for(register int j=(i<<1);j<=400000;j+=i) if(!mark[j]) mark[j]=i;//当时不会写欧拉筛,不过埃式筛同样可以胜任功能:Dscanf("%d",&T);while(T--){scanf("%d",&n),cntp=0;for(register int i=0;i<n;++i){scanf("%d",a+i);if(!mark[a[i]]) ++cntp,ans=a[i];}if(cntp>1) ans=-1;else{if(!cntp) ans=2;for(register int i=0;i<n;++i){if(ans^a[i]&&!(a[i]&1)&&(ans<<1)>a[i]){// printf("ans=%d a[i]=%d 0\n",ans,a[i]);ans=-1;break;}if(ans^a[i]&&(a[i]&1)&&a[i]-mark[a[i]]<(ans<<1)){// printf("ans=%d a[i]=%d 1\n",ans,a[i]);ans=-1;break;}}}printf("%d\n",ans);}return 0;
}
解题思路
该代码的目的是找出一个数组中所有元素的最大公约数,并输出这个最大公约数以及它在数组中出现的次数。
在 main 函数中,首先读取 n 和 m,表示数组的大小和最大公约数的上限。
然后读取数组 a,并统计每个数出现的次数。
使用两个嵌套循环来计算每个数的倍数出现的次数,并更新最大公约数和出现次数。
最后,输出最大公约数和它在数组中出现的次数,并输出数组中所有能被最大公约数整除的元素的下标。