P10219 [省选联考 2024] 虫洞 题解
前三个条件说明对于每种编号构成的子图都是形如若干个环,于是这启发我们对于每种颜色分别处理。考虑现在已经处理了编号为 \(1\sim i-1\) 的边,考虑加入编号为 \(i\) 的边,看什么条件下会合法。
不难发现合法的添加有两种:
-
在一个连通块 \(G=(V,E)\) 中加边。加边方式形如一个循环移位(即一个大环)。并且可以发现当一个点的连边被确定后,整个连通块的加边方案就确定了。所以方案数为 \(|V|\)。
-
在从连通块 \(G_1=(V_1,E_1)\) 向连通块 \(G_2=(V_2,E_2)\) 连边。为了满足第四个条件,这两个连通块应该是同构的(同构是指可以对两个联通块中的点进行重标号使得这两个连通块相同,显然一个必要条件为 \(|V_1|=|V_2|\land |E_1|=|E_2|\))。同理,方案数为 \(|V_1|\)。
由此我们可以发现两个性质:
-
对于任意连通块,它是强连通的。
-
如果两个连通块一开始不同构,那么以后他们不可能在同构。
所以在一开始可以将同构的连通块放在一起单独处理。发现转移的代价仅与连通块点数有关,这启示我们忽略其连通块具体构造而仅记录其点数进行处理。
设 \(f_{i,j}\) 表示将 \(i\) 个有 \(j\) 个点的连通块添加 \(K\) 种边的方案数。假设我们将同构的联通块放在一起形成若干组 \((G,|V|,cnt)\),则答案为 \(\prod f_{cnt,|V|}\)。
现在考虑如何求 \(f\)。
由于 \(f\) 的图中个连通块最后不一定合并成一个连通块,用一般图计数的思路,枚举第 \(n\) 个点在的连通块,化为处理连通图计数问题。
设 \(dp_{k,i,j}\) 表示添加了 \(k\) 种边,有 \(i\) 个含 \(j\) 个点的连通块,并最终合并成一个连通块的方案数,枚举第 \(i\) 个连通块所在的那个连通块,有转移:
现在考虑如何求 \(dp_{}\)。
枚举合并为几个连通块,有转移 \(dp_{k,i,j}=\sum_{x|i}dp_{k-1,x,\frac {ij}x}g_{i,x}res\)
其中 \(g_{i,j}\) 表示将 \(i\) 个点分为 \(j\) 个圆排列的方案数。考虑每次选出 \(\frac ij\) 个点进行圆排列的过程,方案数为 \(\frac{i!}{\frac ij(i-\frac ij)!}\times \frac{(i-\frac ij)!}{\frac ij(i-2\frac ij)}\times \cdots=\frac{i!}{(\frac ij)^j}\) 由于圆排列之间是无序的,再除以 \(j!\) 最终方案数为 \(\frac{i!}{j!(\frac ij)^j}\)。
\(res\) 表示一次连边合并为 \(x\) 块,且两两同构的方案数。对于第 \(1\) 块里面的 \(\frac jx\) 可以随便连边,即 \(j^{\frac ix}\) 种,对于剩下的 \(x-1\) 块,前 \(\frac ix-1\) 可以随便连,最后一个必定可以使得整个图同构(画图可以理解),即 \(j^{(\frac ix-1)(x-1)}\) 种。两者乘起来为 \(j^{i-x+1}\) 种。
于是:
设 \(h_{k,i,j}=\frac{dp_{k,i,j}}{j^{i}}\),整理可得 \(h_{k,i,j}=j\sum_{x|i}h_{k-1,x,j\times \frac {i}x}\frac{i!}{x!(\frac ix)^x}\),发现这次转移 \(h_{k,i,j}\) 相比 \(h_{k,i,1}\) 仅是多乘了一个 \(j\) ,而其第三维所有可以到的状态也是 \(\frac ix\) 与 \(j\times \frac ix\) 即乘了一个 \(j\) 的区别,于是可以发现性质:\(h_{k,i,j}=j^{k-1}h_{k,i,1}\),进一步可得:
设 \(q_{i,j}=dp_{i,j,1}\),则有:
设 \(p_{i,j}=\frac{q_{i,j}}{(j-1)!j^{i-1}}\),则有:
????????将 \(p_{i,j}\) 设作\(\frac{q_{i,j}}{(j-1)!j^{i}}\),列出方程\(p_{i,j}=\frac 1j\sum_{x|j}p_{i-1,x}\) 能否卷积?可以,但卷积式子竟然不变



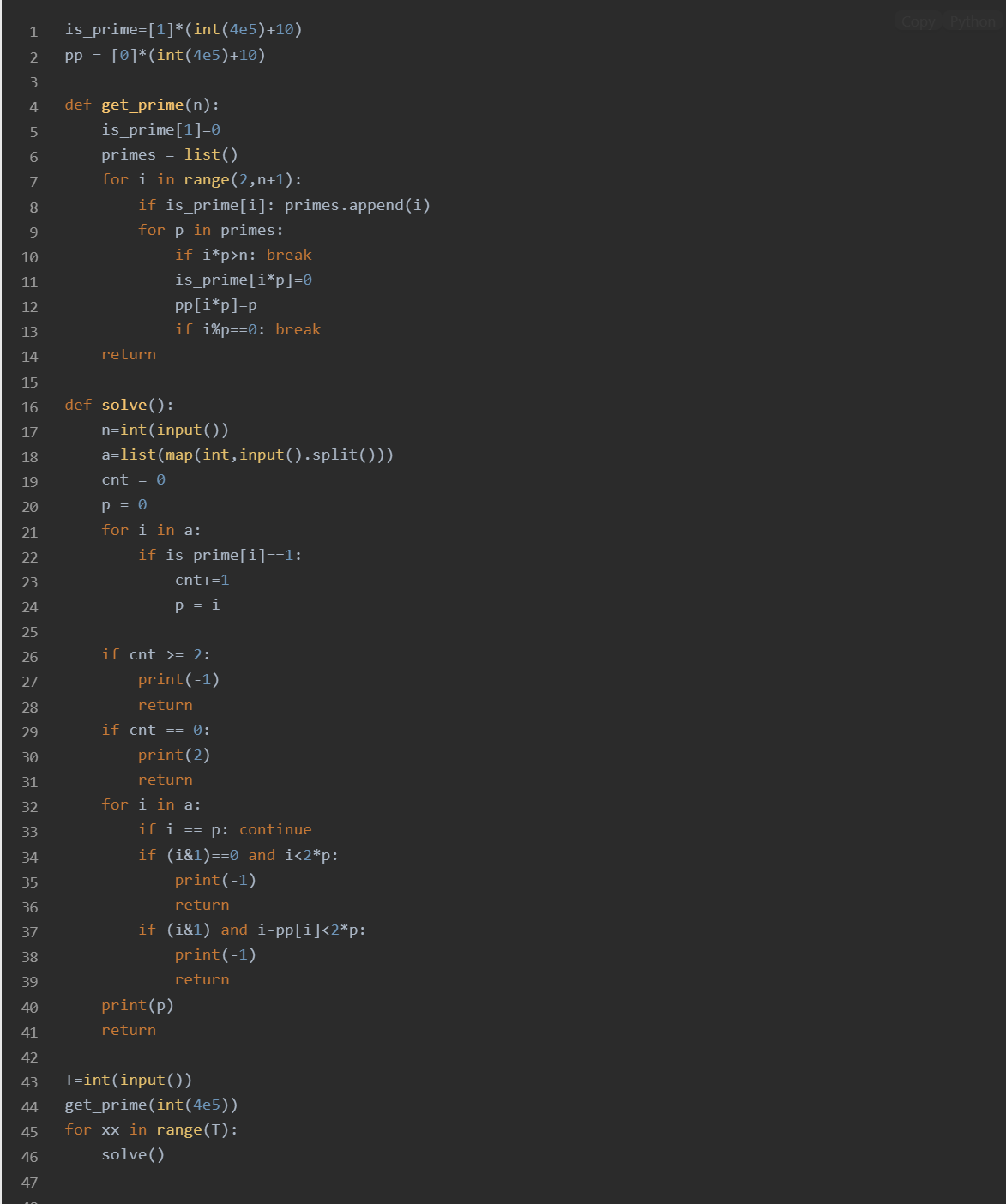

![P1314 [NOIP 2011 提高组] 聪明的质监员(前缀和)](https://img2024.cnblogs.com/blog/3599636/202502/3599636-20250210204754315-1131463956.png)