Luogu P1600 NOIP2016提高组 天天爱跑步 题解 [ 紫 ] [ 线段树合并 ] [ 树上差分 ]

天天爱跑步：这题主要难点还是想到根据 lca 分成两边，分讨算贡献。

思路

首先看到树上路径，很容易就能想到树上差分计算每个跑步的人的贡献。

那么一个人的贡献改如何计算呢？我们考虑某个观察员他在 \(w\) 秒到底能观察到谁，显然是能观察到路线经过他且到他的距离为 \(w\) 的人。

因此，我们就可以根据路径上每个点到起点的距离来计算贡献。

而由于起点和终点的 lca 两边的点的距离计算方式不相同，所以需要进行分类讨论：

当路径未经过 lca 时

这时候观察员 \(x\) 能观察到人的条件是 \(dep_s-dep_x=w_x\)，把有关观察员的变量全部丢到一边，得到 \(dep_s=dep_x+w_x\)。

当路径经过 lca 时

这时候观察员 \(x\) 能观察到人的条件是 \(dep_s-dep_{lca}+dep_x-dep_{lca}=w_x\)，把有关观察员的变量全部丢到一边，得到 \(dep_x-w_x=2\times dep_{lca}-dep_s\)。

于是，我们就可以开桶记录下每个值对应的贡献，查询的时候答案就是 \(dep_x+w_x\) 的贡献与 \(dep_x-w_x\) 的和。同时注意特判 \(w_x=0\) 的情况，此时直接将两者的贡献相加会导致贡献多算一倍。

这个桶我们可以用动态开点线段树实现，然后做树上前缀和求答案的时候直接线段树合并即可。

注意这个线段树会存负数下标，且树上差分的时候要先在 lca 处减掉未经过 lca 的贡献，在 lca 的父亲处再减掉经过 lca 的贡献，不然会导致未经过 lca 的贡献被减两次或者经过 lca 的贡献被减两次。

时间复杂度 \(O(n\log n)\)，因为树上差分一个操作要修改四次，所以空间记得开四倍。

代码

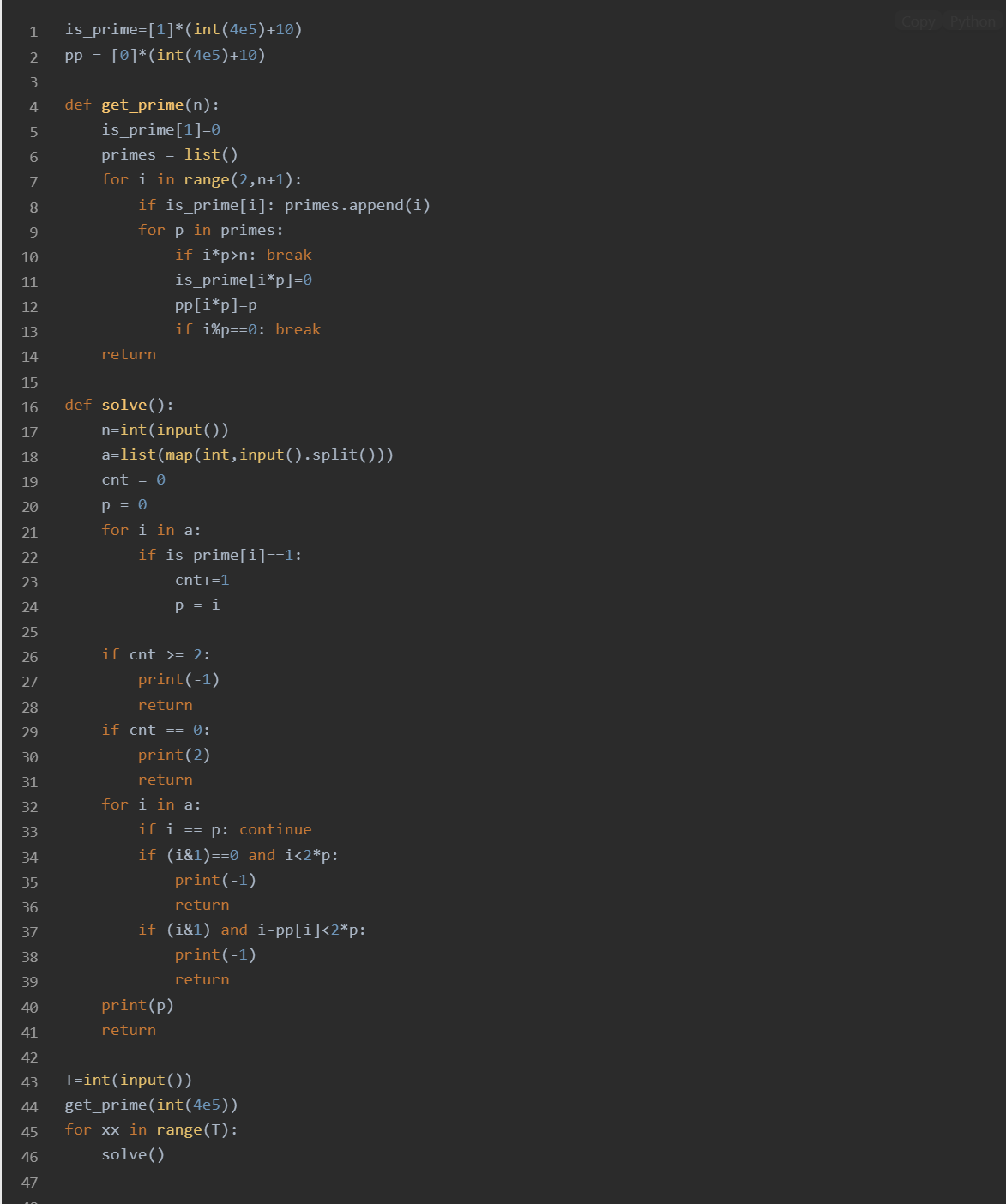
#include <bits/stdc++.h>
#define fi first
#define se second
#define eb(x) emplace_back(x)
#define pb(x) push_back(x)
#define lc(x) (tr[x].ls)
#define rc(x) (tr[x].rs)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
using pi=pair<int,int>;
const int N=300005;
int n,m,w[N],fa[N],top[N],dep[N],sz[N],son[N],ans[N];
vector<int>g[N];
struct Node{int ls,rs,v;
};
struct Segtree{Node tr[80*N];int root[N],tot=0;void update(int &u,int ln,int rn,int x,int k){if(u==0)u=++tot;tr[u].v+=k;if(ln==rn)return;int mid=(ln+rn)>>1;if(x<=mid)update(lc(u),ln,mid,x,k);else update(rc(u),mid+1,rn,x,k);}int merge(int x,int y){if(x==0||y==0)return x+y;tr[x].v+=tr[y].v;tr[x].ls=merge(lc(x),lc(y));tr[x].rs=merge(rc(x),rc(y));return x;}int query(int u,int ln,int rn,int x){if(ln==rn)return tr[u].v;int mid=(ln+rn)>>1;if(x<=mid)return query(lc(u),ln,mid,x);else return query(rc(u),mid+1,rn,x);}
}tr1;
void dfs1(int u,int f)
{dep[u]=dep[f]+1;fa[u]=f;sz[u]=1;for(auto v:g[u]){if(v==f)continue;dfs1(v,u);sz[u]+=sz[v];if(sz[son[u]]<sz[v])son[u]=v;}
}
void dfs2(int u,int tp)
{top[u]=tp;if(son[u]==0)return;dfs2(son[u],tp);for(auto v:g[u]){if(v==fa[u]||v==son[u])continue;dfs2(v,v);}
}
int getlca(int u,int v)
{while(top[u]!=top[v]){if(dep[top[u]]<dep[top[v]])swap(u,v);u=fa[top[u]];}if(dep[u]<dep[v])swap(u,v);return v;
}
void dfs3(int u,int f)
{for(auto v:g[u]){if(v==f)continue;dfs3(v,u);tr1.root[u]=tr1.merge(tr1.root[u],tr1.root[v]);}ans[u]=tr1.query(tr1.root[u],-N,N,dep[u]+w[u]);if(w[u])ans[u]+=tr1.query(tr1.root[u],-N,N,dep[u]-w[u]);
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<n;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}dfs1(1,0);dfs2(1,1);for(int i=1;i<=n;i++)cin>>w[i];while(m--){int s,t;cin>>s>>t;int lca=getlca(s,t);int flca=fa[lca];tr1.update(tr1.root[s],-N,N,dep[s],1);tr1.update(tr1.root[t],-N,N,2*dep[lca]-dep[s],1);tr1.update(tr1.root[lca],-N,N,dep[s],-1);tr1.update(tr1.root[flca],-N,N,2*dep[lca]-dep[s],-1);}dfs3(1,0);for(int i=1;i<=n;i++)cout<<ans[i]<<" ";return 0;
}