上一讲中我们介绍了对极几何的相关知识,在这一讲开头我们先回顾一下平行图像平面的对极几何。
平行图像平面的对极几何(Parallel image planes)

在这种情况下,对应点的极线是水平的,光心连线与图像平面的交点(极点)在无穷远处,并且在这种平行配置下,同一个三维点在两个图像平面上投影点的 y 坐标是相等的,这些特殊的性质对我们恢复结构很有帮助。
图像校正(Rectification)

如图所示,图像校正也就是让两幅图像平行,校正前的两幅图像,其中物体的对应关系较为复杂,极线(图中虚线)并不平行。这是从两个不同视角拍摄的同一场景,能看到物体的相对位置和角度存在差异,而校正后的图像此时极线变得平行,图像中的物体仿佛在同一平面上对齐。这通过应用单应性变换(Homogra-phy,图中用 H 表示)实现,它对图像进行了几何变换,将图像平面调整到平行状态。
这种做法也给我们带来了许多的好处:
\(\bullet\) 使对应问题变得更容易:在立体视觉中,寻找两幅图像中的对应点是关键任务,平行图像中对应点位于同一水平极线上,只需在水平方向搜索,大幅简化了匹配过程。
\(\bullet\) 使三角测量变得容易:三角测量用于从两个或多个视角的图像来计算三维点的位置,平行图像的规则几何关系让基于视差的三角测量计算更简便。
\(\bullet\) 支持图像插值方案:图像插值是根据已知像素值估计未知像素值,平行图像的规律性为设计有效的插值算法提供了便利,有助于提高图像分辨率或填补图像缺失部分等操作。
深度计算(Computing depth)
深度计算是上述方法的一个特别经典的应用。

-
P:三维空间中的一个点。
-
O 和 O':两个相机的光心,它们之间的距离为基线(baseline),用 B 表示。
-
u 和 u':点P在两个相机成像平面上的投影点的横坐标。
-
f:相机的焦距。
-
z:点P到相机光心的深度距离。
-
公式 $ u - u'=\frac{B\cdot f}{z} = \text{disparity} $。其中, $ u - u' $ 表示视差(disparity),它是同一个点在两个相机图像平面上投影点的横坐标之差。
-
视差与深度成反比,也就是说,物体离相机越远(深度 $ z $ 越大),视差越小;物体离相机越近(深度 $ z $ 越小),视差越大。
通过测量同一点在两个不同视角图像中的视差,并结合已知的相机焦距和基线长度,就可以计算出该点在三维空间中的深度。
对应问题(Correspondence problem)
本节课的重点是对应问题:给定三维空间中的一个点,找出它在左右图像中的对应观测点(也称为双目融合问题)。对应问题是立体视觉中的关键问题。其核心在于如何准确地匹配三维空间中的同一个点在不同视角(这里是左右两个相机视角)图像上的投影点。解决这个问题对于后续的深度计算、三维重建等任务至关重要,因为只有确定了对应点,才能基于视差原理计算出点的深度信息。
正如前文所述,当我们对图像进行校正后,这个问题将变得非常简单。
解决这类问题有三种方法:
-
A Cooperative Model (Marr and Poggio, 1976):合作模型(马尔和波焦,1976 年)。这是一种早期用于解决对应问题的模型,由 Marr 和 Poggio 在 1976 年提出。
-
Correlation Methods (1970--):相关方法(始于 1970 年)。这类方法通过计算图像块之间的相关性来寻找对应点,是 20 世纪 70 年代开始应用于解决对应问题的一类经典方法。
-
Multi - Scale Edge Matching (Marr, Poggio and Grimson, 1979 - 81):多尺度边缘匹配(马尔、波焦和格里姆森,1979 - 1981 年)。该方法由 Marr、Poggio 和 Grimson 在 1979 - 1981 年间提出,通过在不同尺度上匹配图像的边缘信息来解决对应问题。
本文将详细介绍第二种方法。

假设我们的每一个点都有一个特征值,为了在右图中寻找左图中的点的对应点,我们需要找到一个点使得它与左图中的点的特征值最为接近,实际上,这个问题其实是一个相关性匹配的问题。
具体的操作步骤如图所示,图中不同颜色表示图像点具有不同的特征值,首先我们需要在图像 1 中以点 \(\bar{p}=(\bar{u}, \bar{v})\) 为中心选取一个窗口 \(W\),然后将窗口 \(W\) 内的像素信息或特征信息按一定顺序排列成向量形式。接着在图像 2 中沿 \(v = \bar{v}\) 滑动窗口 \(W'\) ,并对每个位置构建向量 \(w'\),最后对图像 2 中窗口 \(W'\) 滑动到的每个 \(u\) 位置,计算向量 \(w\) 和 \(w'\) 的点积,保留最大值,该最大值对应的位置即为图像 1 中点 \(\bar{p}\) 在图像 2 中的可能对应点。
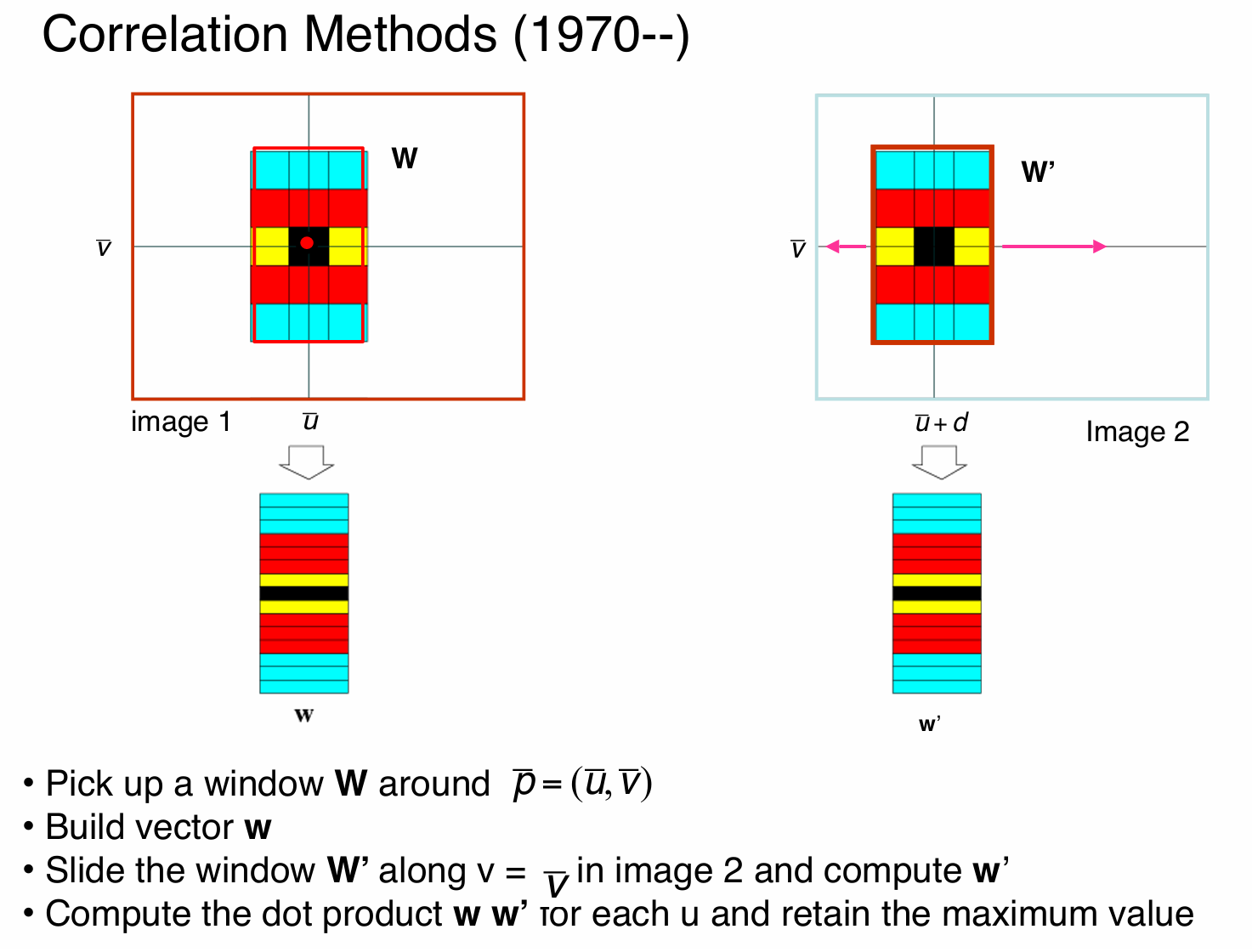
但是这种做法也存在一些问题,比如两幅图像由于亮度或者曝光的变化,两张图像中对应区域(窗口)的像素强度值的统计特性(均值和方差)也会发生改变,这种变化可能会对相关方法产生影响,导致匹配错误或性能下降。
为了解决该问题,人们对算法进行了改进,如图所示:
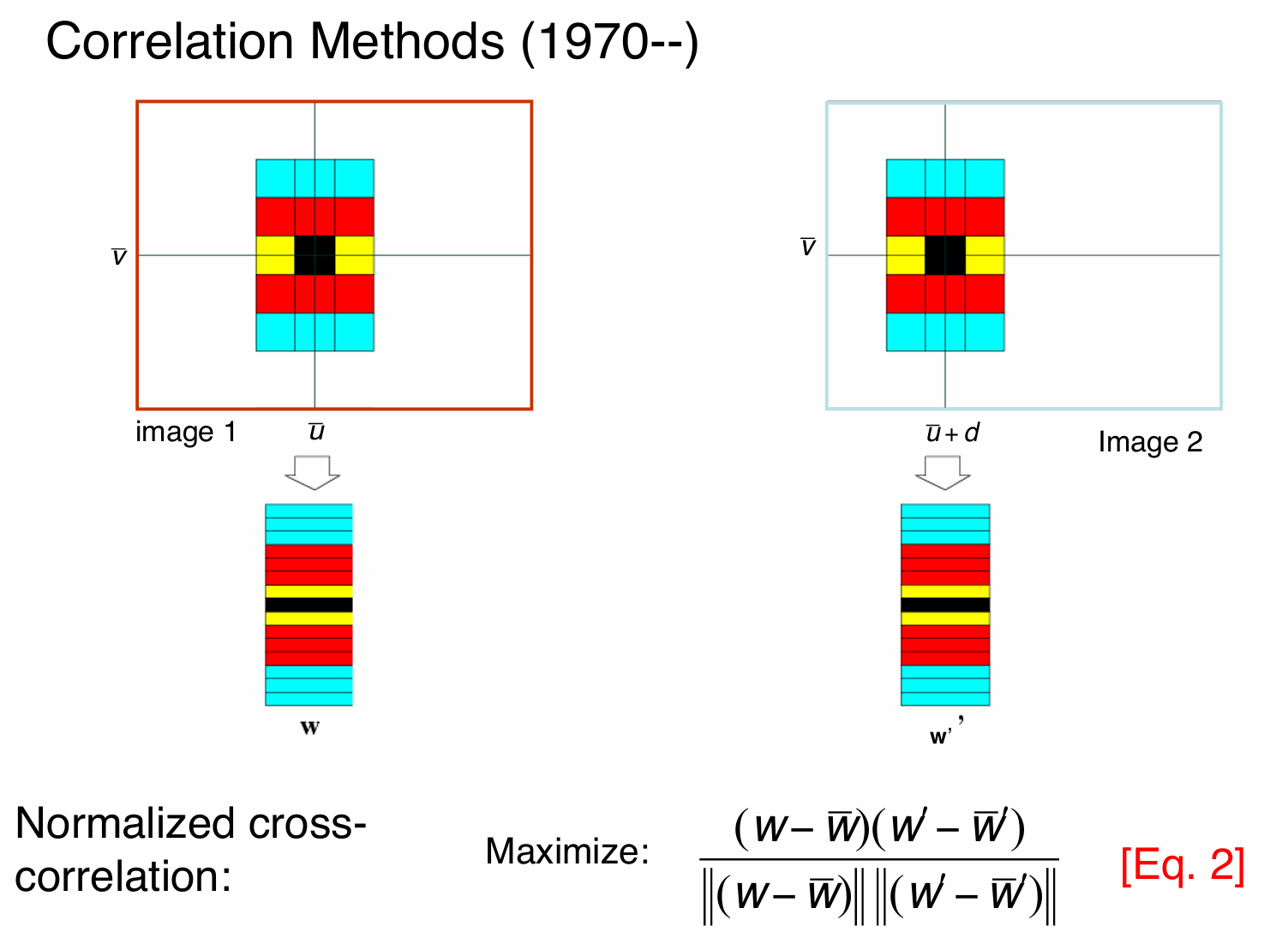
我们采用归一化互相关的方法,通过最大化归一化互相关的计算结果来寻找最佳匹配,即最大化:
\(
\frac{(W - \bar{W})(W' - \bar{W}')}{\|(W - \bar{W})\|\|(W' - \bar{W}')\|}
\)
其中,\(W\) 和 \(W'\) 分别是图像 1 和图像 2 中的窗口,\(\bar{W}\) 和 \(\bar{W}'\) 分别是它们的均值。
该公式用于计算两个窗口之间的归一化互相关值。通过最大化这个值,可以确定图像 1 中的点在图像 2 中的对应点。这种方法相比简单的相关方法,对光照变化等因素具有更强的鲁棒性,因为它对窗口内的像素值进行了归一化处理。
对于上述方法,窗口大小的选择对于结果有着很大的影响,选取小的窗口能够保留图像中的细微特征,但由于覆盖范围小,也容易受到局部噪声影响。选取大的窗口能够得到更平滑的视差图,在计算视差等任务中,大窗口能使结果更平滑,并且不易受噪声影响,对局部噪声有一定的平均抑制作用。因此窗口大小的选择是一个权衡细节和噪声的过程,需根据具体需求进行调整。
对应问题中存在的问题
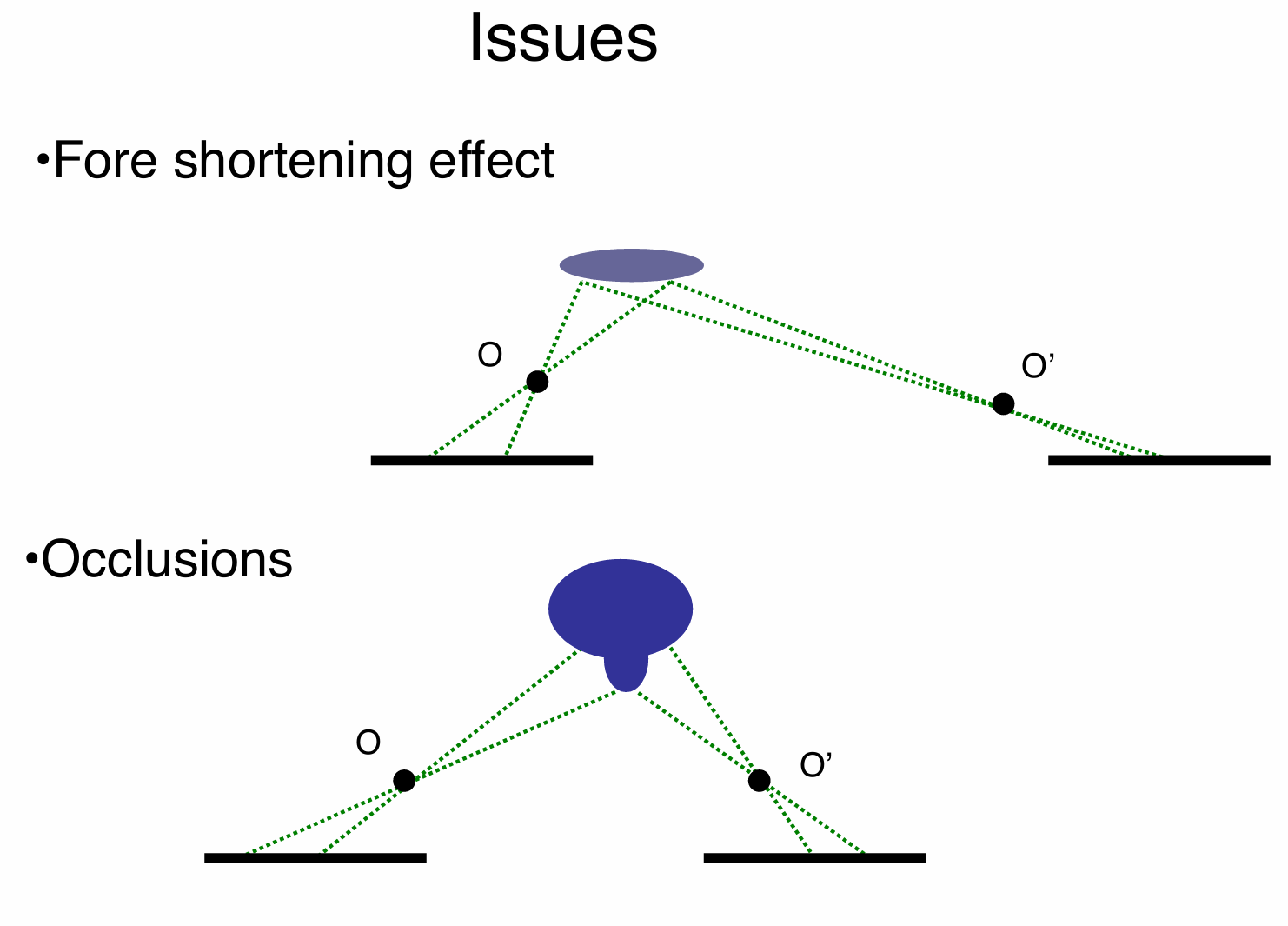
- 透视缩短效应(Fore shortening effect)
有一个倾斜的物体(用紫色椭圆表示),由于物体的倾斜角度,在两个相机成像平面上的投影会出现透视缩短现象,即物体在图像中的尺寸和形状会因视角不同而发生变化,这会给立体匹配带来困难。
- 遮挡(Occlusions)
存在一个遮挡物(用蓝色不规则图形表示),它阻挡了部分场景在相机中的成像。对于被遮挡的区域,一个相机能看到,但另一个相机可能看不到,导致在立体匹配时难以找到对应的点。
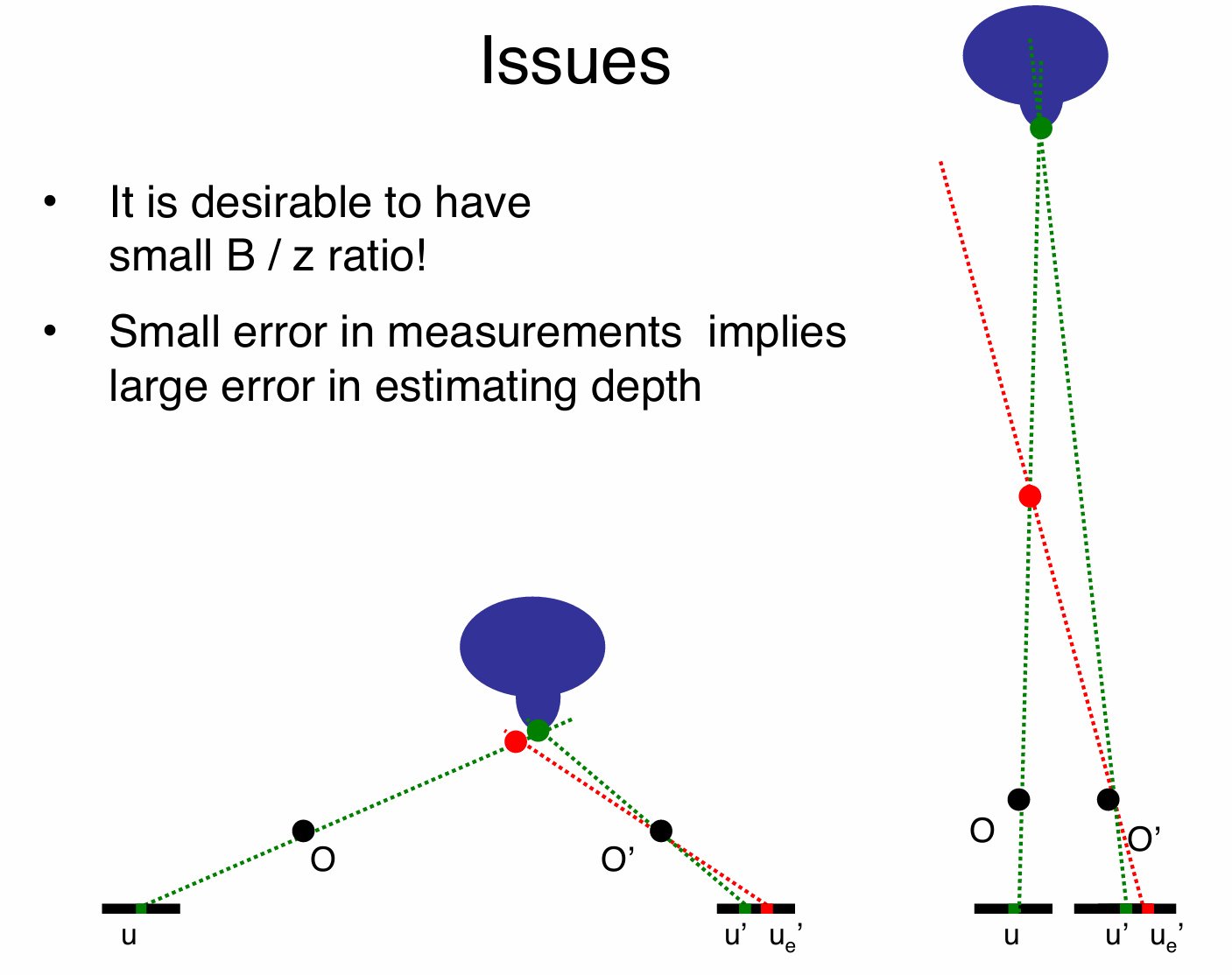
在立体深度估计中,我们希望有较小的 B/z 比值。其中 B 通常代表两个相机光心之间的基线距离(baseline),z 代表物体到相机的深度距离。较小的 B/z 比值有利于某些深度估计任务。同时在深度估计过程中,测量的微小偏差可能会导致深度计算结果出现较大的误差。正如上图所示,可以看到,由于测量误差(成像点从 $ u' $ 变为 $ u_{e}' $ ),在估计物体(蓝色部分)的深度时会产生较大偏差(绿色点和红色点在深度位置上的差异)。这些问题反映了在立体视觉深度估计中,精确测量和合适的系统参数(如 B/z 比值)对于获得准确深度信息的重要性。

在两幅图像中存在着同质区域,具有相似的视觉特征。在匹配过程中,由于同质区域的相似性,可能会导致误匹配(mismatch)。即在进行立体匹配时,难以准确区分这些区域中的点,从而产生错误的对应关系。

如果图像中具有重复出现的纹理或结构,这些重复图案会给匹配算法带来挑战。由于图案相似,算法难以准确区分不同位置的相同图案,可能导致误匹配,即无法正确找到两幅图像中对应的点。
上述问题都是当前对应问题中难以解决的问题,解决的思路是应用非局部约束来帮助强化对应关系,可以引入非局部的约束条件,利用图像中更广泛区域的信息来辅助确定对应点,提高匹配的准确性和鲁棒性。
课件中也给出了一些比较常见的非局部约束条件:
-
Uniqueness(唯一性):对于一幅图像中的任何一个点,在另一幅图像中最多应该有一个匹配点。这一约束确保了匹配的唯一性,避免一个点对应多个点的模糊匹配情况。
-
Ordering(顺序性):对应点在两个视图中应该具有相同的顺序。例如,在左图像中从左到右的一系列点,在右图像中的对应点也应保持相同的从左到右的顺序,这有助于在匹配过程中利用点的顺序关系来验证匹配的正确性。
-
Smoothness(平滑性):视差通常是 x 的平滑函数(遮挡边界除外)。意味着在场景中,除了在遮挡边界处,相邻点的视差值变化应该是平滑的,不会出现剧烈的跳变。这一约束可以帮助在匹配过程中对相邻点的视差进行合理的推断和约束。
这些非局部约束条件常用于辅助计算机视觉算法在处理对应问题时,更准确地建立图像之间的点对应关系,提高匹配的精度和可靠性。
以上就是本节课的全部内容,如有问题,请指正。