一、微分
用求导来得到微分,也就是函数的变化量。
一阶导数:求一阶导数,之前在校时,大部分人接触它,主要是为了求极值。也就是另f`(x)=0的时候,这个x代入后的f(x)就是极值。实际上,求一阶导数,几何意义就是求变化率,所以,对于路程求时间的导数,就是速度,对于一个曲线,求x的导数,就是斜率。当f`(x)=0的时候,可以求驻点,驻点,可以理解为,在此处,函数的切线,是与x轴平行的,所以和x平行,对于二次函数来说,它可能是最高点,也可能是最低点,如果不是二次函数或者是个不规律的函数,它可能既不是最大值也不是最小值(拐点)。所以驻点,可能是极值点(最大值,最小值),也可能是拐点;
二阶导数:二阶导数的存在,主要意义就是进一步确定,刚刚那个驻点,是极值(极大值还是极小值?),还是拐点。f`(x)=0时,当f``(x)>0,代表从左向右,从负变成正了,所以就是最小值,这是个凹函数;当f``(x)<0,代表从左向右,从正变成负了,所以就是最大值,这是个凸函数;如果f``(x)=0,代表是个拐点,就是这个点两侧,凹凸性发生了变化,有深入研究需求的话,就还要继续分析。
引申:拐点,在测试工作的质量分析中,有很常见的应用。比如我们平时对bug趋势图分析,会需要观察拐点出现的个数和位置,以此来推算整个研发过程的健康性。比如拐点数目理论上应该和每个迭代包的数目匹配(出现在每一个新的迭代包发行的时间点),每个迭代包bug的发现趋势,应该是先上升(凹函数)然后趋于平和,最终下降(凸函数),这个变化的点,就是拐点。每个迭代包都应该是这样的一个bug发现趋势。进一步,会根据拐点出现的早晚,分析产品的测试情况是否健康,比如,拐点出现太早,刚上升就下降了,这代表质量真得好,或者测试方法、工具出现问题,早早就测不出来了。后者的可能性通常是更大的。如果修正了测试方法、工具,极大概率会立刻迎来一个拐点,就是bug再次迅速上升了;或者拐点出现太晚,说明质量太差了,也可能是测试同学测high了,提了太多建议性bug,这种也一定要干预。如果是质量问题,就要研发经理赶紧注意督促代码质量,是测试问题,测试代表也要尽快了解和干预,否则就不要结项了。
二、积分
分为定积分和不定积分。
不定积分:其实就是反向求导,把f`(x)求出来f(x)的过程。对应上面一阶求导的一些物理意义,你可以理解为,根据速度,我求一下距离;
定积分:几何意义,可以理解为,就是函数在某个区间内,和x轴(如果是基于x求导)围成的面积。其中,F(x)其实是f(x)原函数。因此解定积分使用的牛顿-莱布尼茨公式,也可以很明确地说明微分和积分的关系。对f(x)反向求导,就得到了原函数F(x),然后在[a,b]这个区间里,函数和x轴围成的面积,就是积分。
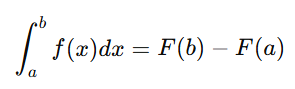
记录一道题,帮助日后快速回忆: