AC截图:

1、自然数的拆分问题
数据范围很小,直接dfs暴力枚举就行。
#include <iostream>
using namespace std;int n;
int arr[10];void dfs(int x, int sum , int start)
{if (sum > n){return;}if (sum == n && x != 2){for (int i = 1 ; i <= x-1 ; i++){if (i <= x-2){cout << arr[i] << "+";}else{cout << arr[i];}}cout << endl;return;}for (int i = start ; i <= n ; i++){arr[x] = i;dfs(x+1,sum+i,i);}
}int main()
{cin >> n;dfs(1,0,1);
}
2、填涂颜色
本题关键在于找到闭合圈。首先找到第一个1出现的行,下一行第一个1后的0即闭合圈首个元素。将该元素加入队列bfs即可覆盖整个闭合圈。
#include <iostream>
#include <queue>
using namespace std;int g[40][40];
bool st[40][40];
int n;
int dx[] = {1,0,-1,0};
int dy[] = {0,1,0,-1};
typedef pair<int,int> PII;void bfs(int x , int y)
{queue<PII> q;q.push({x,y});st[x][y] = true;while (!q.empty()){PII t = q.front();q.pop();for (int i = 0 ; i <= 3 ; i++){int a = t.first + dx[i];int b = t.second + dy[i];if (a < 1 || b < 1 || a > n || b > n) continue;if (st[a][b] == true) continue;if (g[a][b] == 1) continue;st[a][b] = true;q.push({a,b});}}
}int main()
{cin >> n;bool flag1 = false;bool flag2 = false;int x1,y1,x2,y2;for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= n ; j++){cin >> g[i][j];if (flag1 == false && g[i][j] == 1){x1 = i;y1 = j;flag1 = true;}if (flag1 == true && flag2 == false && g[i][j] == 0 && i > x1 && j >= y1){flag2 = true;x2 = i;y2 = j;}}}bfs(x2,y2);for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= n ; j++){if (st[i][j] == false){cout << g[i][j] << " ";}else{cout << 2 << " ";}}cout << endl;}return 0;
}
3、显示图像
从黑点出发找到最近的白点比较麻烦。正难则反,将所有白点加入队列bfs,一定能保证白点首次经过黑点时是最近距离。
#include <iostream>
#include <string>
#include <vector>
#include <cstring>
#include <math.h>
#include <queue>
using namespace std;typedef pair<int,int> PII;
const int N = 3e4;
string g[N];
vector<int> ans[N];
queue<PII> q;
int dx[] = {1,0,-1,0};
int dy[] = {0,1,0,-1};
int n,m;int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;for (int i = 1 ; i <= n ; i++){string str;cin >> str;str = "0" + str;g[i] = str;}for (int i = 1 ; i <= n ; i++){ans[i].push_back(0);for (int j = 1 ; j <= m ; j++){if (g[i][j] == '0') ans[i].push_back(-1);else{ans[i].push_back(0);q.push({i,j});}}}while (!q.empty()){PII t = q.front();q.pop();for (int i = 0 ; i <= 3 ; i++){int x0 = t.first + dx[i];int y0 = t.second + dy[i];if (x0 < 1 || y0 < 1 || x0 > n || y0 > m) continue;if (ans[x0][y0] != -1) continue;ans[x0][y0] = ans[t.first][t.second] + 1;q.push({x0,y0});}}for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= m ; j++){cout << ans[i][j] << " ";}cout << endl;}
}
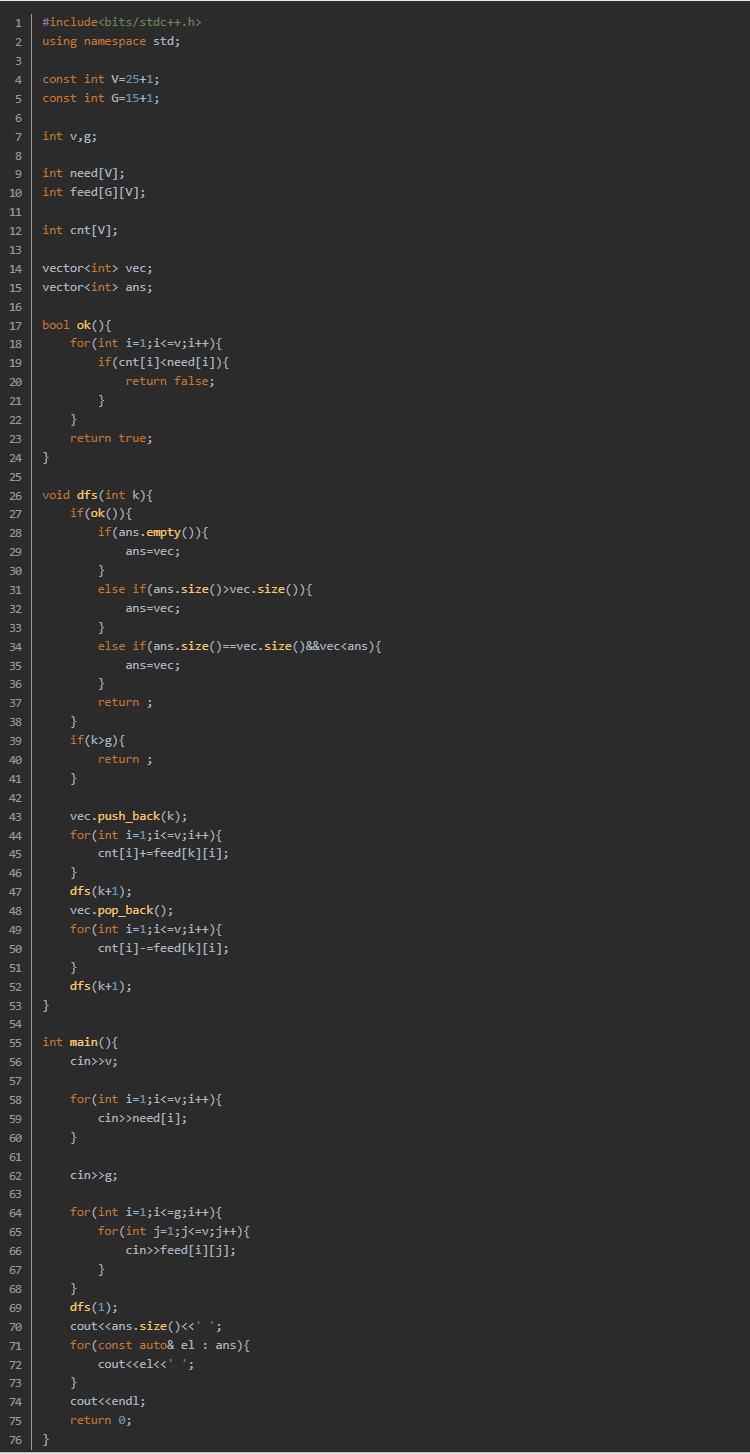
4、健康的荷斯坦奶牛
数据范围并不大,可以直接枚举所有情况。需要注意的是,若当前选择饲料数大于等于先前选择的最优解时,直接剪枝。并且由于从1开始进行01枚举,一定能保证最终方案满足字典序最小。
#include <iostream>
using namespace std;const int N = 30;
int v[N],v1[N]; //所需
int res[N],now[N];
int g[N][N];
int n,m;
int ans = 2e9;void dfs(int x , int cnt)
{if (cnt >= ans) return;if (x > m){for (int i = 1 ; i <= n ; i++){v1[i] = 0;for (int j = 1 ; j <= cnt ; j++){int pos = now[j];v1[i] += g[pos][i];}if (v1[i] < v[i]) return;}for (int i = 1 ; i <= cnt ; i++) res[i] = now[i];ans = min(ans,cnt);return;}now[cnt+1] = x;dfs(x+1,cnt+1);dfs(x+1,cnt);
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n;for (int i = 1 ; i <= n ; i++) cin >> v[i];cin >> m;for (int i = 1 ; i <= m ; i++){for (int j = 1 ; j <= n ; j++){cin >> g[i][j];}}dfs(1,0);cout << ans << " ";for (int i = 1 ; i <= ans ; i++){cout << res[i] << " ";}return 0;
}
5、GRZ-Ridges and Valleys
从一个点开始bfs,找到所有与其高度相等的位置,类似并查集的思想,将它们都指向父节点,构成一个集合。再判断每个集合周围元素是否满足山峰或山谷条件。需要特判当整个图高度都相等的情况。
#include <iostream>
#include <queue>
using namespace std;typedef pair<int,int> PII;
const int N = 1010;
int g[N][N];
int pre[N][N];
int dx[] = {-1,0,1,1,1,0,-1,-1};
int dy[] = {1,1,1,0,-1,-1,-1,0};
queue<PII> q;
int n,ans1,ans2,cnt;void bfs(int x , int y)
{q.push({x,y});pre[x][y] = cnt;bool flag1 = false; //更低bool flag2 = false; //更高while (!q.empty()){PII t = q.front();q.pop();for (int i = 0 ; i <= 7 ; i++){int x0 = t.first + dx[i];int y0 = t.second + dy[i];if (x0 < 1 || y0 < 1 || x0 > n || y0 > n) continue;if (pre[x0][y0] == pre[x][y]) continue;if (g[x0][y0] == g[t.first][t.second]){pre[x0][y0] = cnt;q.push({x0,y0});}else if (g[x0][y0] > g[t.first][t.second]) flag2 = true;else flag1 = true;}}if (flag1 && !flag2) ans1++;if (flag2 && !flag1) ans2++;return;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n;bool flag = true; //全部相同int f = 0;for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= n ; j++){cin >> g[i][j];if (flag){if (i == 1 && j == 1) f = g[i][j];else{if (g[i][j] != f) flag = false;}}}}if (flag){cout << 1 << " " << 1 << endl;return 0;}for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= n ; j++){if (!pre[i][j]){cnt++;bfs(i,j);}}}cout << ans1 << " " << ans2 << endl;
}
6、八皇后
本题要求每行每列只有一个棋子很好处理,难点在于对角线。利用主副对角线索引的性质,可以用一个数表示一条对角线。易知,主对角线上x-y为定值,副对角线上x+y为定值。用该定值表示一条对角线即可。剩下的就是dfs枚举每个合法的位置。
#include <iostream>
using namespace std;int cnt = 0;
int n;
int arr[20];
bool st[20]; // 每列状态
bool diag1[40]; // 主对角线
bool diag2[40]; // 副对角线void dfs(int x) {if (x > n) {cnt++;if (cnt <= 3) {for (int i = 1; i <= n; i++) {cout << arr[i] << " ";}cout << endl;}return;}for (int i = 1; i <= n; i++) {if (!st[i] && !diag1[x - i + n] && !diag2[x + i]) {arr[x] = i;st[i] = true;diag1[x - i + n] = true; // 主对角线diag2[x + i] = true; // 副对角线dfs(x + 1);st[i] = false;diag1[x - i + n] = false;diag2[x + i] = false;}}
}int main() {cin >> n;dfs(1);cout << cnt << endl;return 0;
}