ACM寒假集训第五次专题任务
一、自然数的拆分问题
题目:
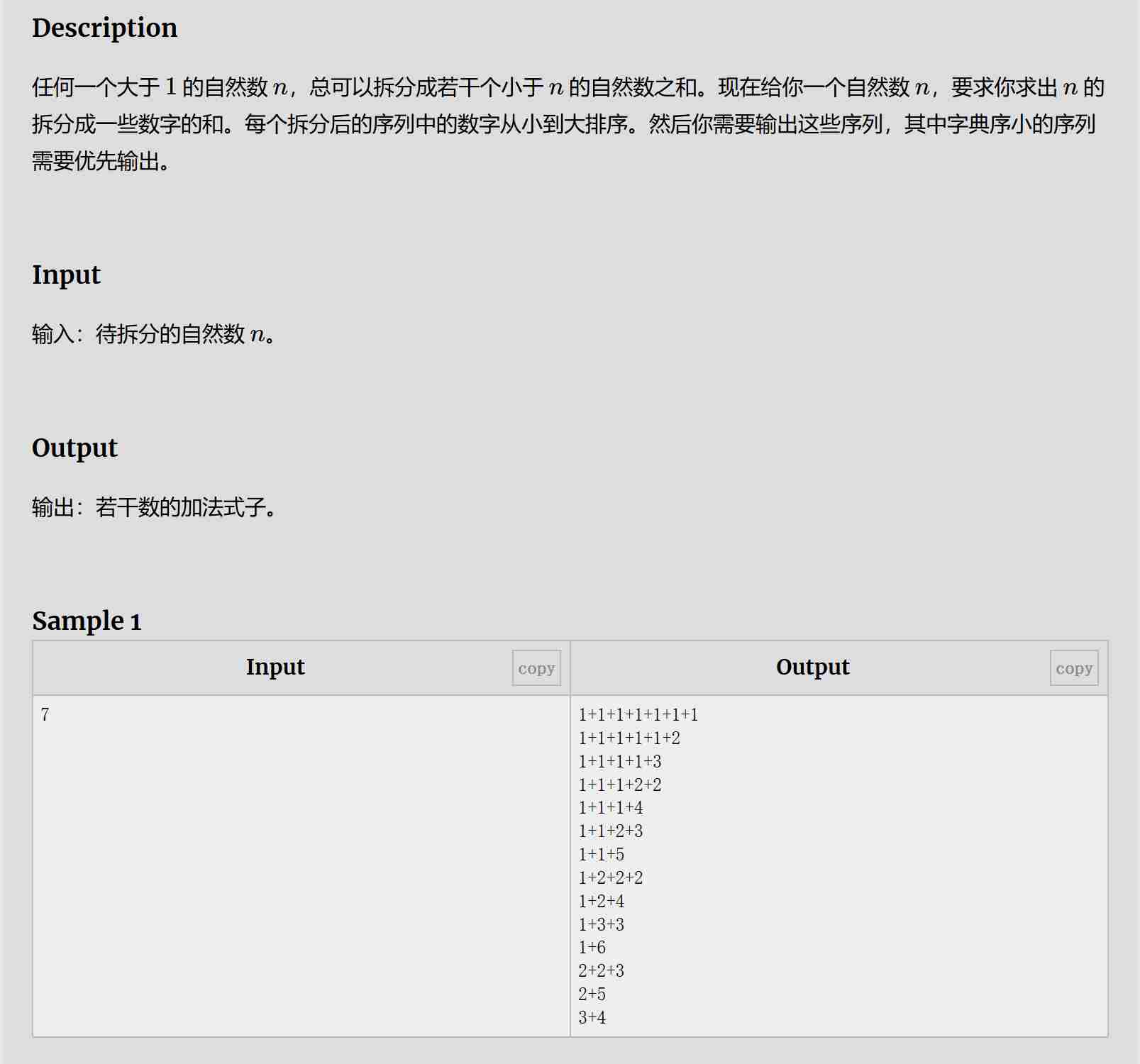

解题思路:
使用了深度优先搜索,通过he判断何时输出,c标记长度控制输出,qs标记起始位置从小到大拆分。
AC代码:
#include<iostream>
using namespace std;
int n,a[10],ans;
void dfs(int he,int c,int qs)
{if(he==n){for(int i=1;i<=c-2;i++){cout<<a[i]<<'+';}cout<<a[c-1]<<endl;return;}else if(he>n){return;}for(int i=qs;i<n;i++){a[c]=i;dfs(he+i,c+1,i);}
}
int main()
{cin>>n;dfs(0,1,1);return 0;
}
二、填涂颜色
题目:
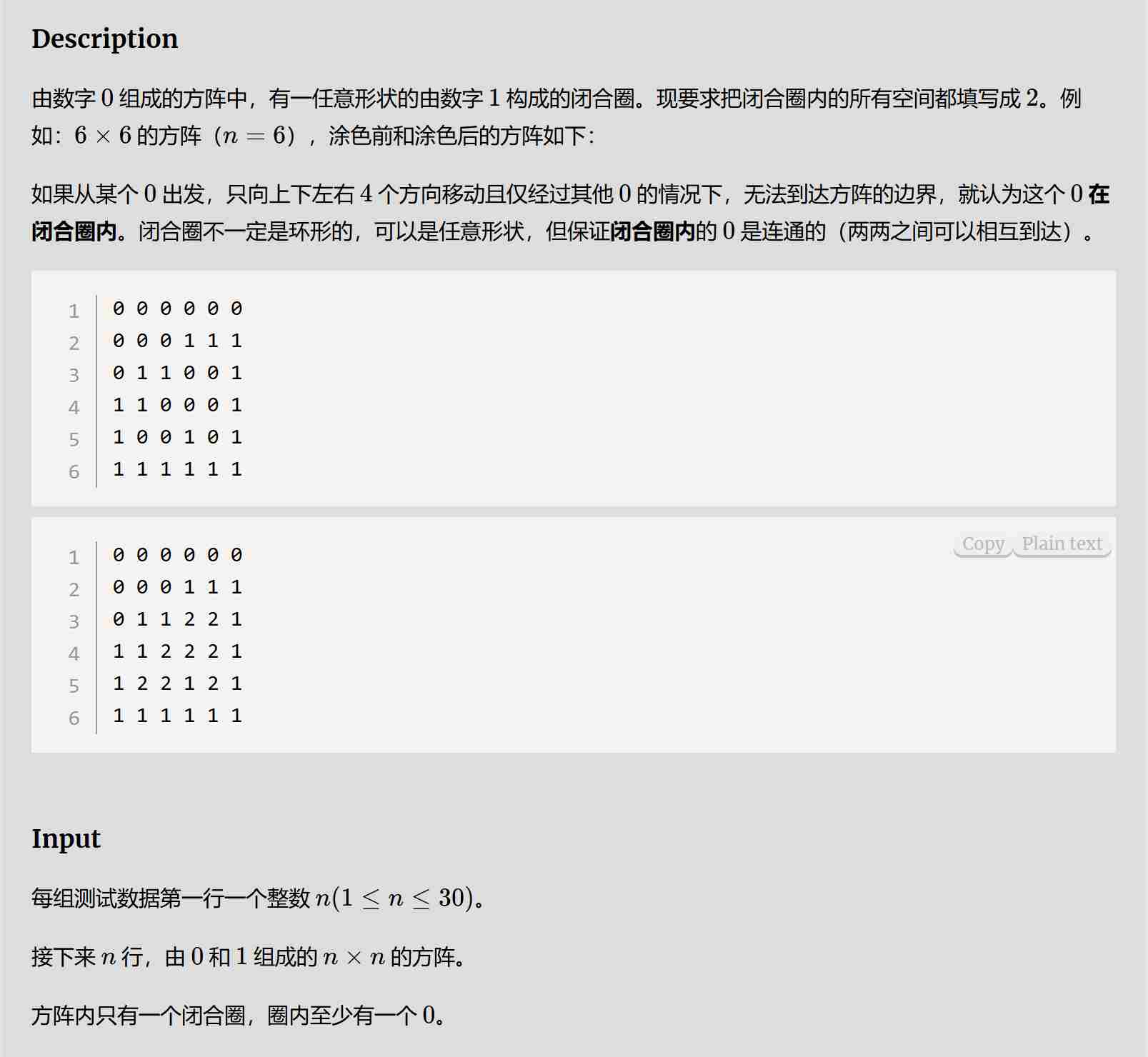
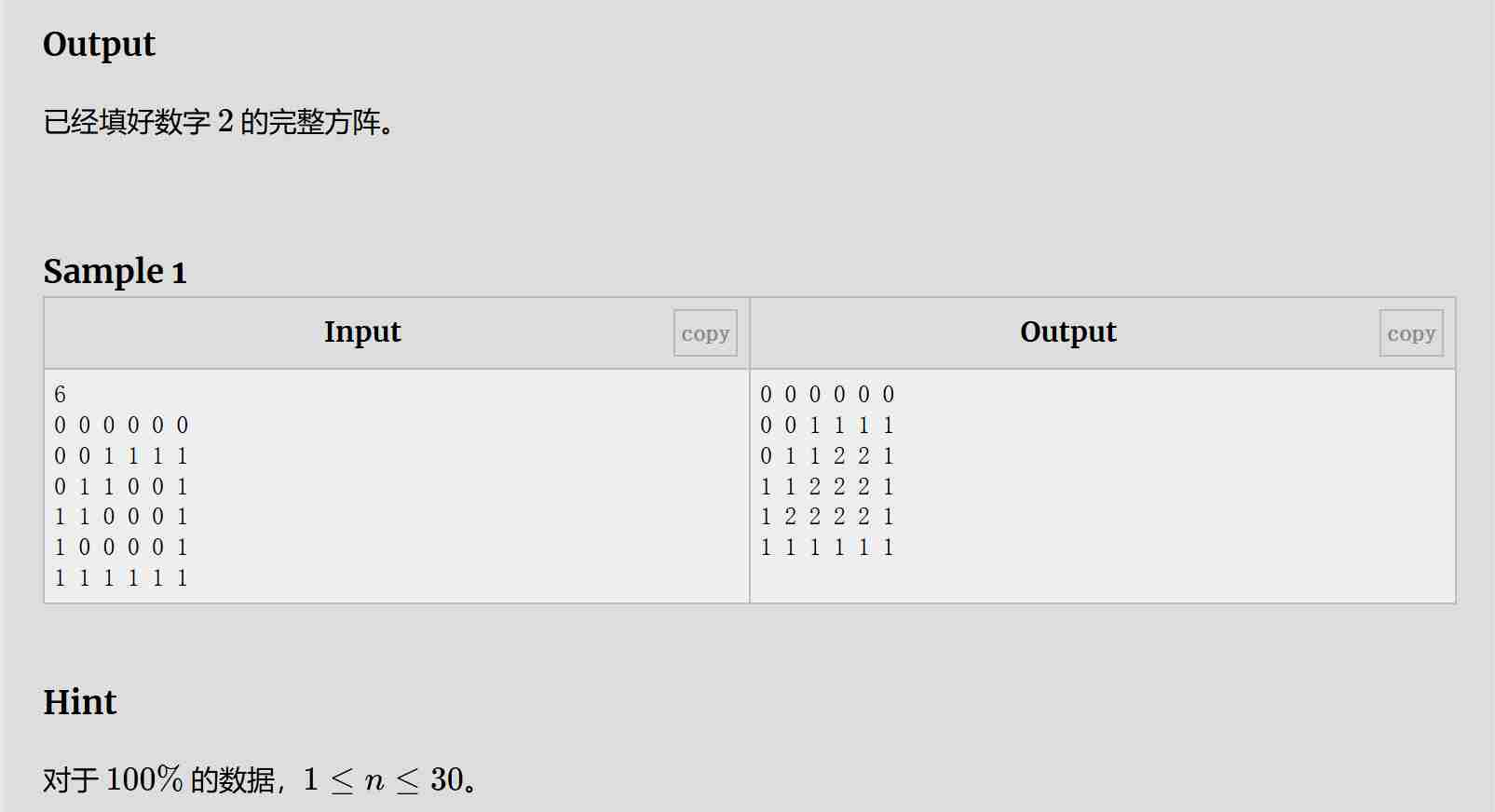
解题思路:
使用了深度优先搜索,将所有边界的0标记成3,再将未被标记的0标记为2,从左上角开始一遍(覆盖与上边界、左边界接触的0),再右下角一遍(覆盖与下边界、右边界接触的0)。
AC代码:
#include<iostream>
#include<cstring>
using namespace std;
int n;
char a[35][35],b[35][35];
void dfs(int x,int y)
{if(a[x][y]=='1'){return;}else if((a[x+1][y]=='3'||a[x-1][y]=='3'||a[x][y+1]=='3'||a[x][y-1]=='3')&&(a[x][y]=='0'||a[x][y]=='2')){a[x][y]='3';return;}else if(a[x][y]=='0'){a[x][y]='2';dfs(x+1,y);dfs(x-1,y);dfs(x,y+1);dfs(x,y-1);}
}
int main()
{cin>>n;memset(a,'3',sizeof(a));for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];b[i][j]=a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dfs(i,j);}}for(int i=n;i>=1;i--){for(int j=n;j>=1;j--){dfs(i,j);if(a[i][j]=='2'){b[i][j]='2';}}}for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){cout<<b[i][j]<<" ";}cout<<endl;}return 0;
}
三、显示图像
题目:

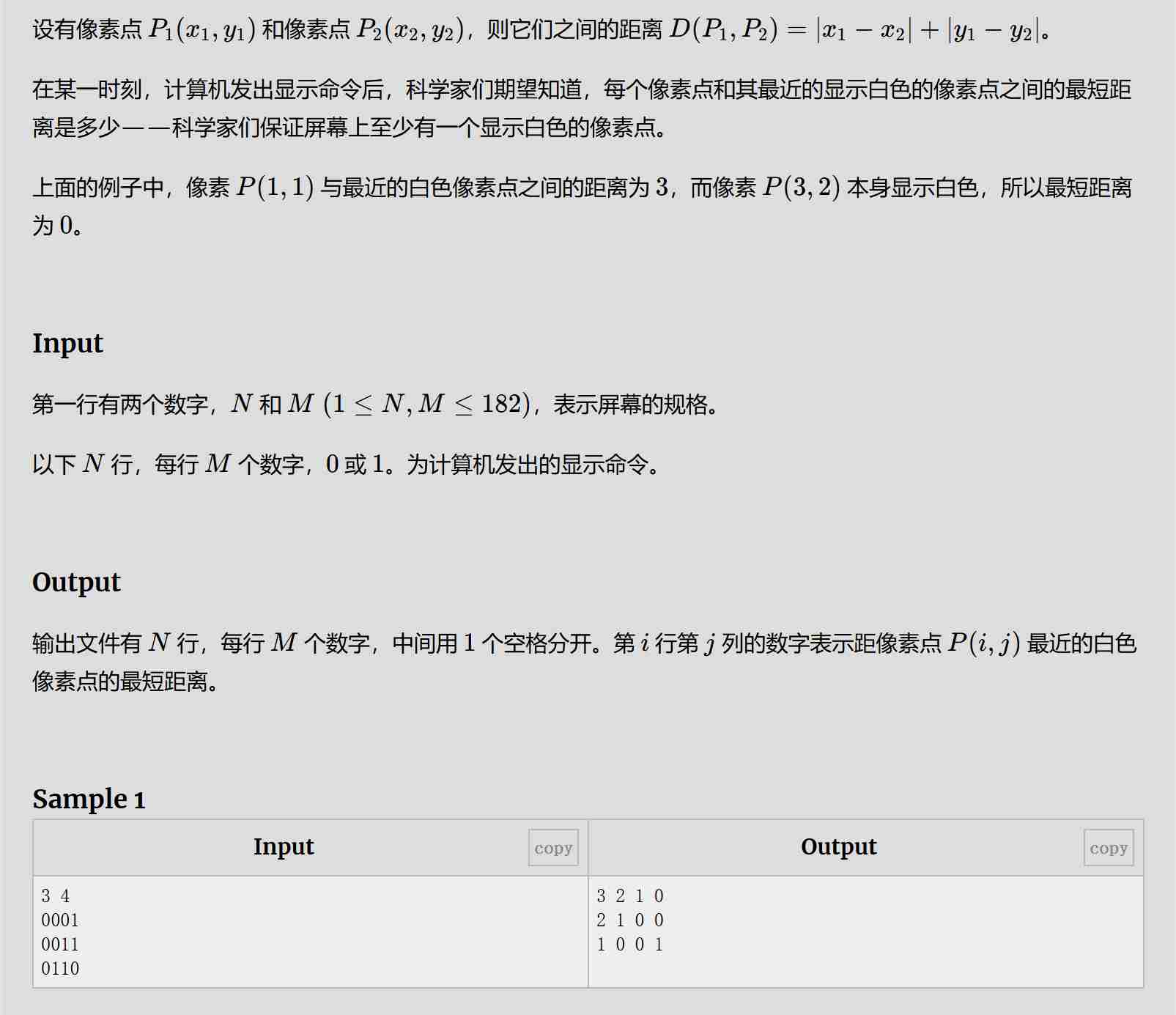

解题思路:
先把所有值为1的点距离设为0,再将其位置依次进队,依次扩展没有计算过距离的点,每次拓展都队头后移,那么队头到1点的距离+1就是拓展的点的距离。
AC代码:
#include<iostream>
#include<cstring>
using namespace std;
int n,m,f[200][200],d[200][200];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
struct node{int x,y;
}a[40000];
int tail,head;
int main()
{cin>>n>>m;memset(f,1,sizeof(f));for(int i=1;i<=n;i++){string s;cin>>s;for(int j=0;j<s.size();j++){if(s[j]=='0'){f[i][j+1]=0;}else{d[i][j+1]=0;f[i][j+1]=1;a[++tail].x=i;a[tail].y=j+1;}}}for(head=1;head<=tail;head++){for(int i=0;i<=3;i++){int xx=a[head].x+dx[i],yy=a[head].y+dy[i];if(!f[xx][yy]){d[xx][yy]=d[a[head].x][a[head].y]+1;f[xx][yy]=1;a[++tail].x=xx;a[tail].y=yy;}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<d[i][j]<<' ';}cout<<endl;}return 0;
}
四、健康的荷斯坦奶牛 Healthy Holsteins
题目:

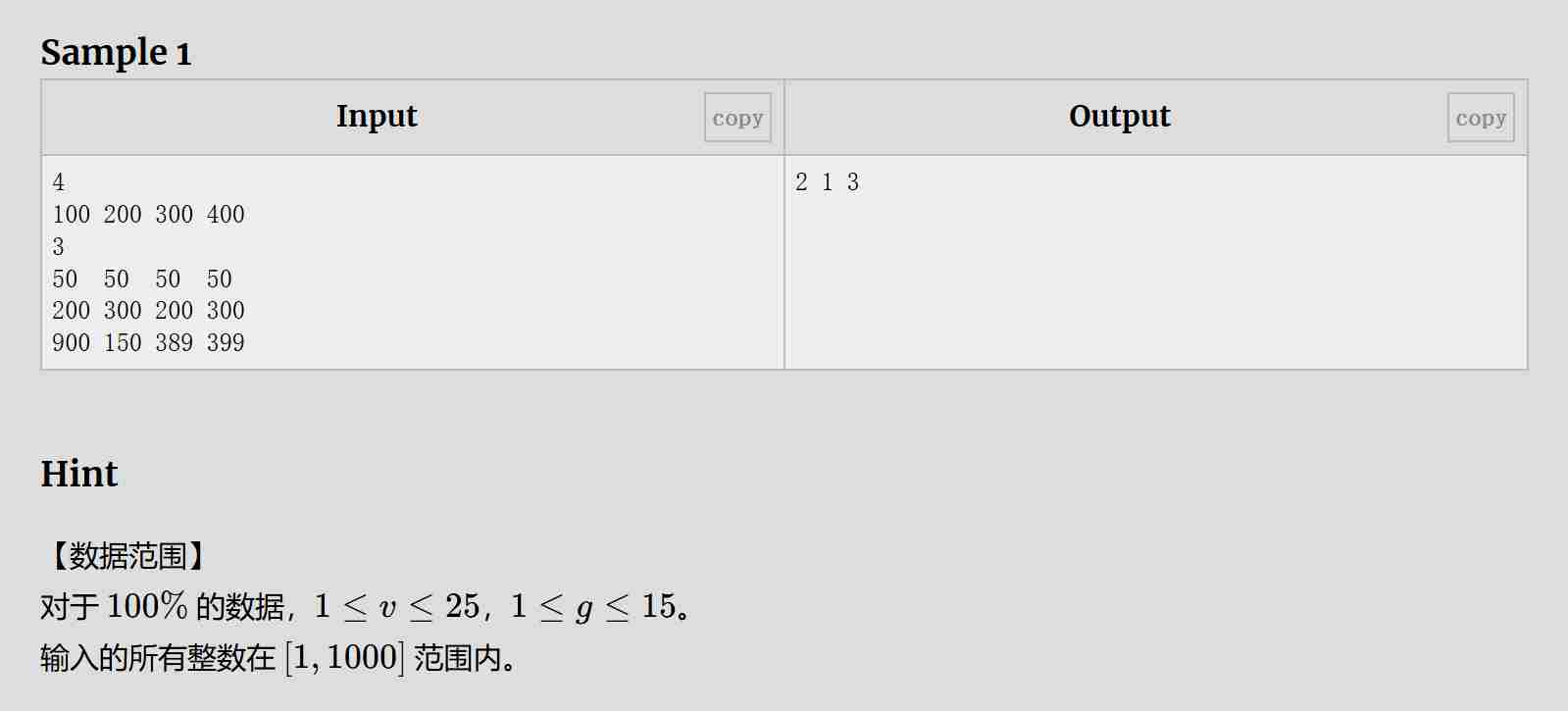
解题思路:
将不同种类维他命相加得出最少种类(深度优先搜索),再判断字典序。
AC代码:
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
vector<int> vec;
vector<int> ans;
const int V=30;
const int G=20;
int v,g;
int need[V];
int feed[G][V];
int cnt[V];
bool ok()
{for(int i=1;i<=v;i++){if(cnt[i]<need[i])return false;}return true;
}
void dfs(int k)
{if(ok()){if(ans.empty()){ans=vec;}else if(ans.size()>vec.size()){ans=vec;}else if(ans.size()==vec.size()&&vec<ans){ans=vec;}return;}if(k>g){return;}vec.push_back(k);for(int i=1;i<=v;i++){cnt[i]+=feed[k][i];}dfs(k+1);vec.pop_back();for(int i=1;i<=v;i++){cnt[i]-=feed[k][i];}dfs(k+1);
}
int main()
{cin>>v;for(int i=1;i<=v;i++){cin>>need[i];}cin>>g;for(int i=1;i<=g;i++){for(int j=1;j<=v;j++){cin>>feed[i][j];}}dfs(1);cout<<ans.size()<<' ';for(const auto& el:ans){cout<<el<<' ';}return 0;
}
五、GRZ-Ridges and Valleys
题目:

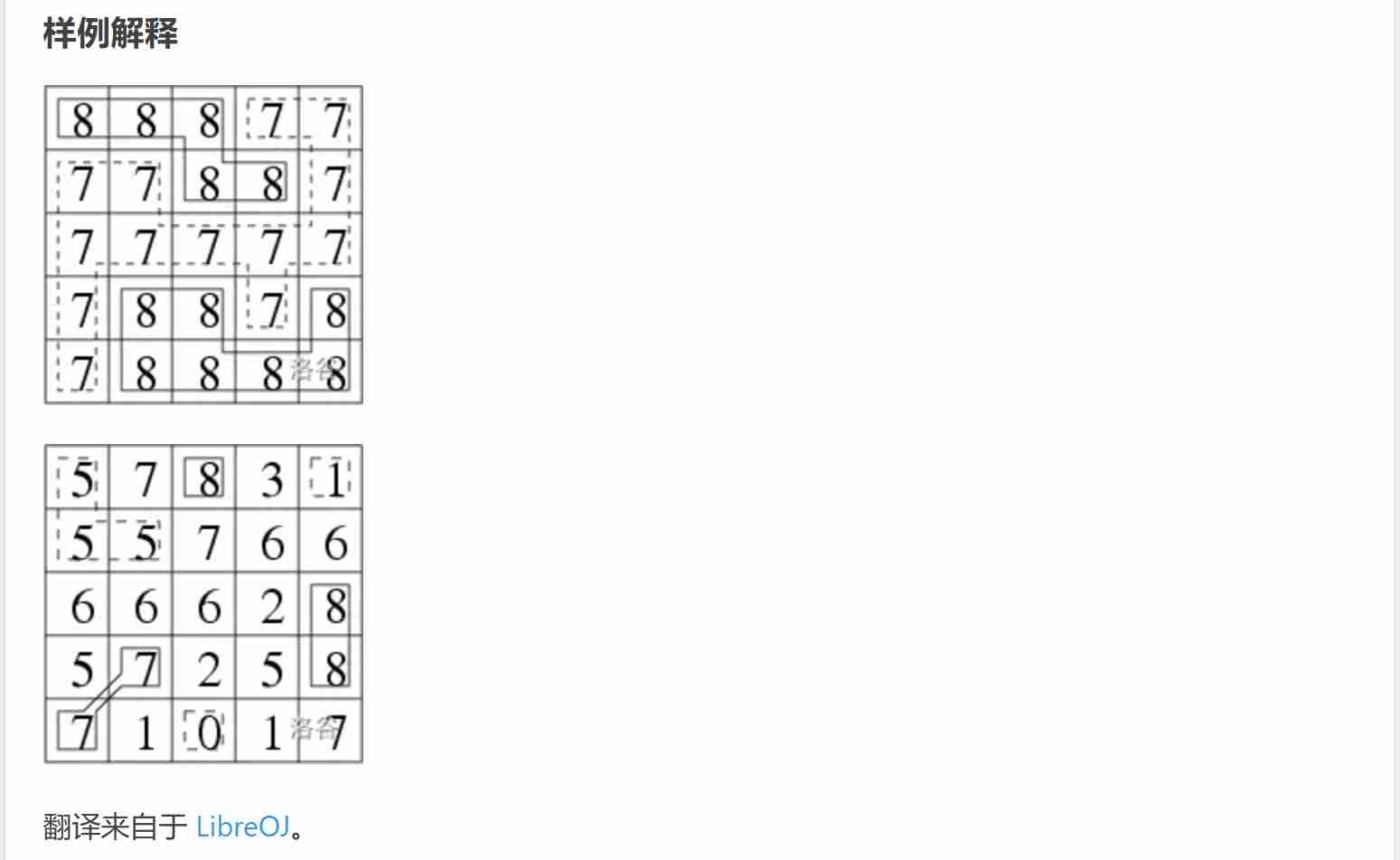
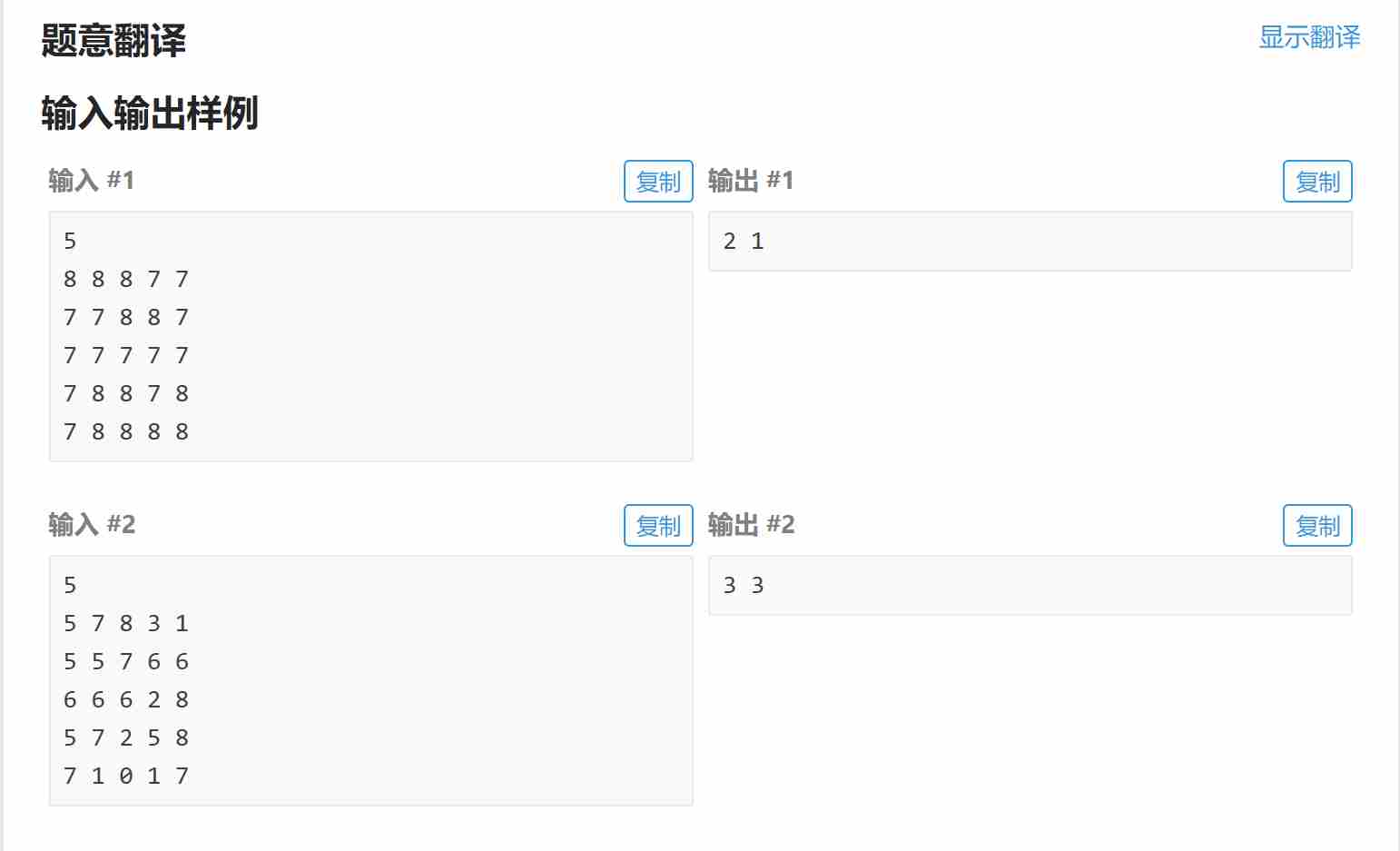
解题思路:
依次搜索连通块周围数字与连通块中数字的大小关系,先假设既是山峰又是山谷,再排除,最后输出结果。
AC代码:
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n;
int dx[]={0,1,0,-1,1,1,-1,-1};
int dy[]={1,0,-1,0,1,-1,1,-1};
int a[1009][1009];
int rcount,vcount;
bool vis[1009][1009];
bool available(int x,int y)
{return x>=1&&x<=n&&y>=1&&y<=n;
}
void bfs(int sx,int sy)
{bool isr=true;bool isv=true;queue<pair<int,int>>Q;vis[sx][sy]=true;Q.push({sx,sy});while(!Q.empty()){int x=Q.front().first;int y=Q.front().second;Q.pop();for(int i=0;i<8;i++){int nx=x+dx[i];int ny=y+dy[i];if(available(nx,ny)){if(a[nx][ny]==a[x][y]&&!vis[nx][ny]){vis[nx][ny]=true;Q.push({nx,ny});}if(a[nx][ny]<a[x][y]){isv=false;}if(a[nx][ny]>a[x][y]){isr=false;}}}}if(isr){rcount++;}if(isv){vcount++;}
}
int main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(!vis[i][j]){bfs(i,j);}}}cout<<rcount<<' '<<vcount;return 0;
}
六、八皇后 Checker Challenge
题目:

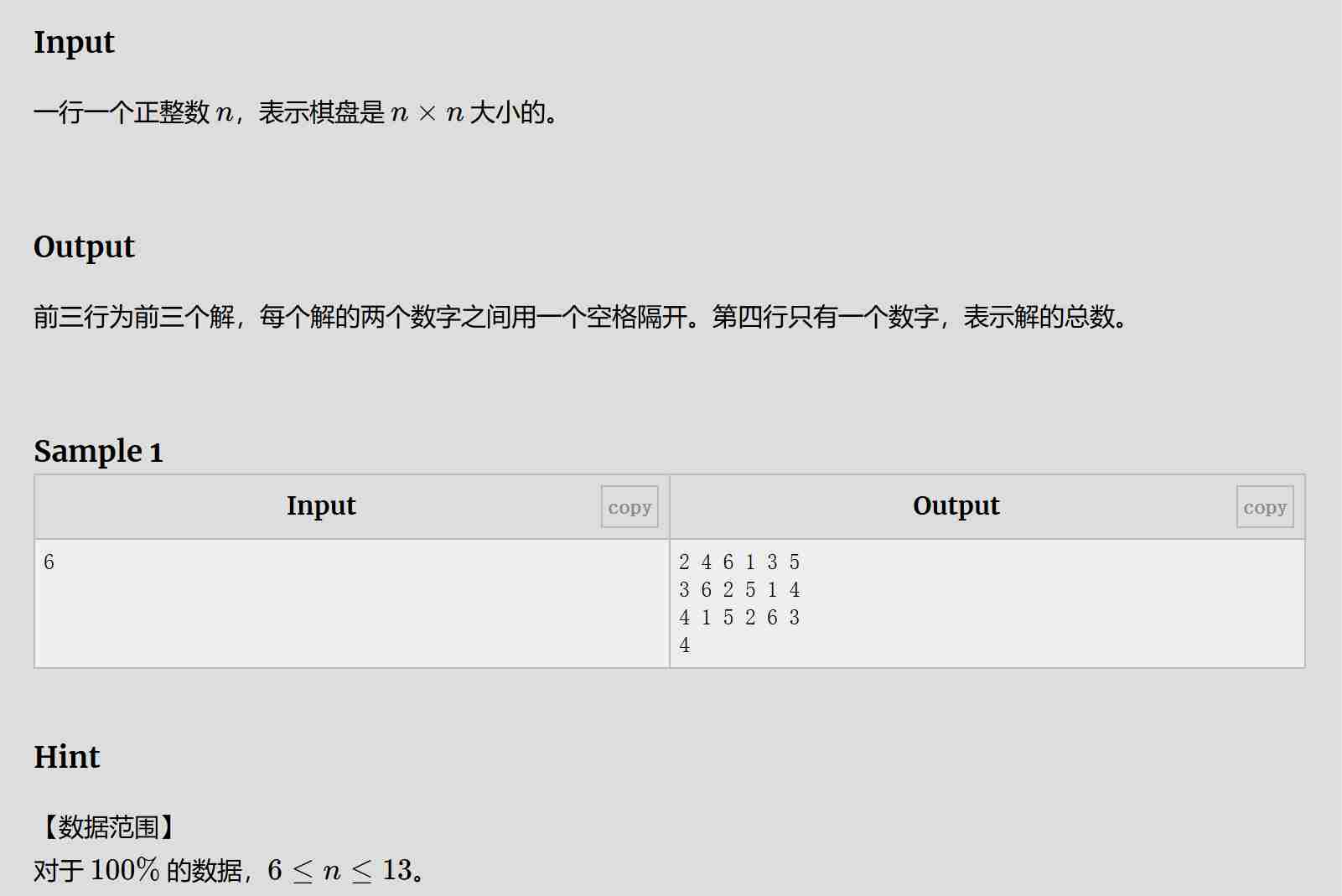
解题思路:
从第一行开始,用行、列、对角线、副对角线进行限制,并对所在行、列、对角线、副对角线进行标记,被标记的行、列、对角线、副对角线不再放棋子。
AC代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=15;
int n,y[N],d1[2*N],d2[2*N];
vector<int>v;
vector<vector<int>>ans;
void dfs(int i)
{if(i>n){ans.push_back(v);return;}for(int j=1;j<=n;j++){if(y[j]==0&&d1[i-j+n]==0&&d2[i+j]==0){y[j]++;d1[i-j+n]++;d2[i+j]++;v.push_back(j);dfs(i+1);v.pop_back();y[j]--;d1[i-j+n]--;d2[i+j]--;}}
}
int main()
{cin>>n;dfs(1);sort(ans.begin(),ans.end());for(int i=0;i<3;i++){for(const auto& el:ans[i]){cout<<el<<' ';}cout<<endl;}cout<<ans.size();return 0;
}
学习总结
深度优先搜索(DFS)与 广度优先搜索(BFS)
图形理解:图的深度优先遍历/深度优先搜索和图的广度优先遍历/广度优先搜索
运用和代码实现:动画演示什么是深搜和广搜 怎么入门搜索算法 这个视频告诉你
对比
| 特性 | 深度优先搜索(DFS) |
广度优先搜索(BFS) |
|---|---|---|
| 实现方式 | 递归或栈 | 队列 |
| 空间复杂度 | 较小 | 较大 |
| 适用问题 | 找到所有可能解、需要回溯的问题 | 最短路径、最短距离问题 |
| 搜索顺序 | 深入一条路径到底,然后回溯 | 逐层扩展,先访问所有相邻节点 |