2.1用二进制数表示计算机信息的原因
IC的所有引脚,只有直流电压0V或5V 两个状态。也就是说,IC的一个引脚,只能表示两个状态。
计算机处理信息的最小单位——位,就相当于二进制中的一位。位的英文bit是二进制数位(binary digit)的缩写。
二进制数的位数一般是8位、16位、32位……也就是8的倍数,这是因为计算机所处理的信息的基本单位是8位二进制数。
8位二进制数被称为一个字节。字节是最基本的信息计量单位。位是最小单位,字节是基本单位。内存和磁盘都使用字节单位来存储和读写数据,使用位单位则无法读写数据。因此,字节是信息的基本单位。(1字节=8位)
用字节单位处理数据时,如果数字小于存储数据的字节数(=二进制数的位数),那么高位上就用0填补。
2.2什么是二进制数

十进制数39的各个数位的数值,并不只是简单的3和9,这点大家应该都知道。3表示的是3×10=30,9表示的是9×1=9。这里和各个数位的数值相乘的10和1,就是位权。数字的位数不同,位权也不同。第1位(最右边的一位)是10的0次幂 (=1),第2位是10的1次幂(=10),第3位是10的2次幂(=100)
构成数值的各数位的数值和位权相乘后再相加的结果。
基数:数值的表现方法,进位计数制中各数位上可能有的数值的个数。
位权的思考方式也同样适用于二进制数。即第1位是2的0次幂(=1),第2位是2的1次幂(=2),第3位是2的2次幂(=4), ……,第8位是2的7次幂(=128)。
“〇〇的××次幂”表示位权,其中,十进制数的情况下〇〇部分为10,二进制数的情况下则为2。这个称为基数 。十进制数是以10为基数的计数方法,二进制数则是以2为基数的计数方法。
“〇〇的××次幂”中的××,在任何进制数中都是“数的位数-1”。即第1位是1- 1=0次幂,第2位是2- 1=1次幂,第3位是3-1=2次幂。
2.3移位运算和乘除运算的关系
移位运算:指的是将二进制数值的各数位进行左右移位(shift=移位)的运算。移位有左移(向高位方向)和右移(向低位方向)两种。在一次运算中,可以进行多个数位的移位操作。
<<这个运算符表示左移,右移时使用>>运算符。<<运算符和>>运算符的左侧是被移位的值,右侧表示要移位的位数。
左移后空出来的低位要进行补0操作。不过,这一规则只适用于左移运算。
移位操作使最高位或最低位溢出的数字,直接丢弃就可以了。

十进制数左移后会变成原来的10倍、100倍、1000倍……同样,二进制数左移后就会变成原来的2倍、4倍、8倍……反之,二进制数右移后则会变成原来的1/2、1/4、1/8……
2.4便于计算机处理的“补数”
二进制数中表示负数值时,一般会把最高位作为符号来使用,因此我们把这个最高位称为符号位。符号位是0时表示正数,符号位是1时表示负数。
为了获得补数,我们需要将二进制数的各数位的数值全部取反 ,然后再将结果加1。例如,用8位二进制数表示- 1时,只需求得1,也就是00000001的补数即可。具体来说,就是将各数位的0取反成1, 1取反成0,然后再将取反的结果加1,最后就转化成了11111111
取反:把二进制数各数位的0变成1,1变成0。
补数求解的变换方法就是“取反+ 1”。
将二进制数的值取反后加1的结果,和原来的值相加,结果为0。
2.5逻辑右移和算数右移的区别
右移有移位后在最高位补0和补1两种情况。当二进制数的值表示图形模式而非数值时,移位后需要在最高位补0。类似于霓虹灯往右滚动的效果。这就称为逻辑右移。
将二进制数作为带符号的数值进行运算时,移位后要在最高位填充移位前符号位的值(0或1)。这就称为算术右移。
如果数值是用补数表示的负数值,那么右移后在空出来的最高位补1,就可以正确地实现1/2、1/4、1/8等的数值运算。如果是正数,只需在最高位补0即可。
以8位二进制数为例,符号扩充就是指在保持值不变的前提下将其转换成16位和32位的二进制数。
2.6掌握逻辑运算的窍门
算术运算:是指加减乘除四则运算。
逻辑运算:是指对二进制数各数字位的0和1分别进行处理的运算,包括逻辑非(NOT运算)、逻辑与(AND运算)、逻辑或(OR运算)和逻辑异或(XOR运算 )四种。
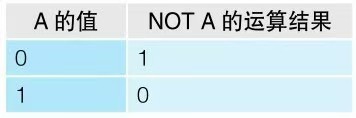
逻辑非:指的是0变成1、1变成0的取反操作。
逻辑与:指的是“两个都是1”时,运算结果为1,其他情况下运算结果都为0的运算。
逻辑或:指的是“至少有一方是1”时,运算结果为1,其他情况下运算结果都是0的运算。
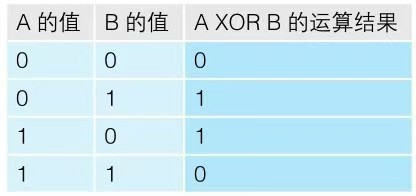
逻辑异或:指的是排斥相同数值的运算。“两个数值不同”,也就是说,当“其中一方是1,另一方是0”时运算结果是1,其他情况下结果都是0。不管是几位的二进制数,在进行逻辑运算时,都是对相对应的各数位分别进行运算。
【真值表】如果将二进制数的0作为假(false)、1作为真(true)来考虑


第二章笔记
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/883435.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
基金年结、结账、关账和开账
基金年结、结账、关账和开账是基金公司年底财务工作中的重要环节,不仅涉及资产、负债、所有者权益等七大要素的核算,还需要进行全面的账务处理和数据校验。本文将详细解读基金年结的背景、目的、概念以及具体流程,帮助大家深入了解这一复杂而关键的财务操作过程。其实年结不…
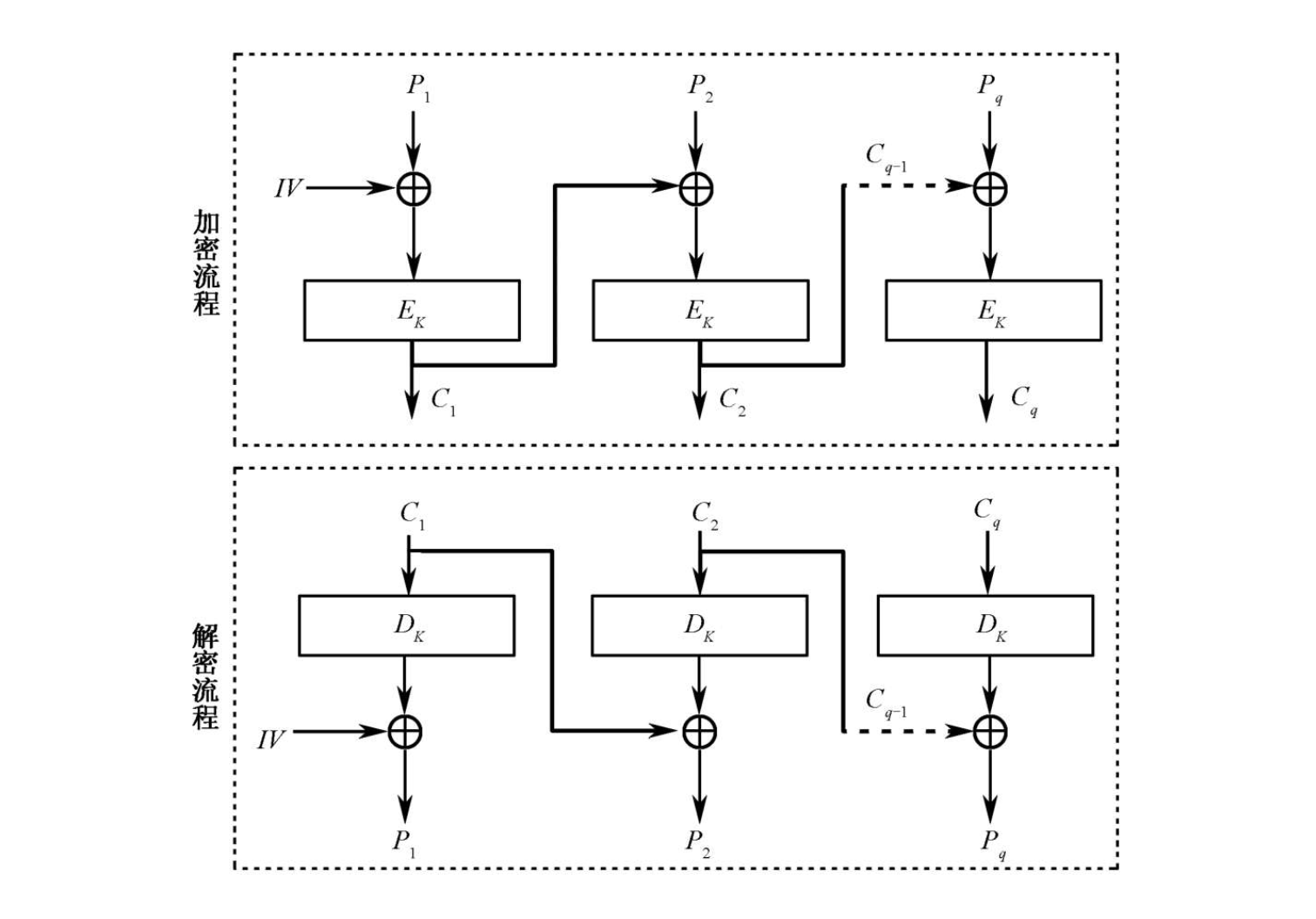
分组密码工作模式-CBC
CBC全称密文分组链接工作模式:是分组密码算法的一种工作模式,其特征是将当前的明文分组与前一密文分组进行异或运算后再进行加密得到当前的密文分组。
在CBC模式下,每个明文分组在加密之前,先与反馈至输入端的前一组密文分组按位异或后,再送至加密模块进行加密。其中,IV是…
基于AutoEncode自编码器的端到端无线通信系统matlab误码率仿真
1.算法仿真效果
matlab2022a仿真结果如下(完整代码运行后无水印):仿真操作步骤可参考程序配套的操作视频。2.算法涉及理论知识概要自编码器是一种特殊的神经网络结构,主要由编码器(Encoder)和解码器(Decoder)两部分组成。自编码器的目标是最小化重构误差,常用的重构误…
2-EasyARM i.MX287A开发板 imx-uboot 主线移植
https://github.com/nxp-imx/linux-imx
这里我们使用 lf-6.1.55-2.2.2 分支开始
首先通过硬件原理图找出 ZLG imx287 和 官方开发板 mx28evk 的差异调试串口
mx28evkZLG287这里可以看到官方板用的GPIO3_16/17作为调试串口,ZLG287 GPIO3_16/17被用作I2C,没有接口引出,DUART使…
国内服务器docker设置代理【2024年12月】在debian12上测试通过
搬运up主凌冰Koori使用export https_proxy这类环境变量已经失效了。现在可以编辑下面的文件:/etc/docker/daemon.json可能对你来说会提示是新文件,不用管。加入以下配置:{“proxies”: {“http-proxy”: “socks5://127.0.0.1:2080”,“https-proxy”: “socks5://127.0.0.1…
Communication Efficient Large-Scale Training with Adams Convergence Speed
目录概1-bit Adam1-bit SGD代码Seide F., Fu H., Droppo J., Li G. and Yu D. 1-bit stochastic gradient descent and its application to data-parallel distributed training of speed dnns. 2014.Tang H., Gan S., Awan A. A., Rajbhandari S., Li C., Lian X., Liu J., Zh…
基于粒子群算法的网络最优节点部署优化matlab仿真
1.程序功能描述基于粒子群算法的网络最优节点部署优化,实现WSN网络的节点覆盖最大化。
2.测试软件版本以及运行结果展示MATLAB2022A版本运行
3.核心程序%使用PSO优化剩余WSN节点位置以覆盖洞
Numv = 2*(N);
func = @(x)fobjs(x,Rmax,area);
Vmin = zeros(Numv,1);…
边坡智能监测识别摄像头
边坡智能监测识别摄像头具备24小时不间断的视频监控能力,可以随时捕捉到边坡的动态变化,并记录所有视频数据。通过深度学习模型,该设备可以自动识别不同类型的异常现象,包括土体位移、裂缝扩展等,大幅提升检测准确率。一旦发现异常情况,系统会立即向相关人员发送警报信息…
AI滴漏监测识别摄像机
AI滴漏监测识别摄像机具备24小时不间断的视频监控能力,可以随时查看现场情况,并记录所有视频数据。一旦检测到液体泄漏,系统会立即向管理人员发送警报信息,以便迅速采取措施进行处理。AI滴漏监测识别摄像机设计坚固,可以在各种复杂环境中稳定工作,包括极端温度、高湿度等…
Fastjson反序列化漏洞原理与漏洞复现
根据这位大佬文章学习
https://blog.csdn.net/Bossfrank/article/details/130100893
Fastjson反序列化
一:json是啥
json是一种格式json全称是JavaScript object notation。即JavaScript对象标记法,使用键值对进行信息的存储。点击查看代码
{"name":"BossFran…