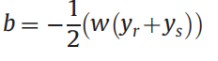2025.2.14鲜花

推歌

（看fengwu博客时候看见的）
《堕》
星河挂在天上 保护璀璨月亮
而你在我心中宛如月光
为你痴为你狂 为你笑为你闯
为你悲为你伤 为你扬
她是踏碎星河落入我梦境的幻想
环遍星系为你寻找的力量
神明给我在最难熬的时光
留下唯一的星光
堕入日月星辉之中梦的信仰
踏碎黎明星照映出的模样
铭憬银河最闪耀的地方
眷恋唯一的星光就是你
海面上风和浪 故事反复发烫
而我在黑暗中就是烈阳
我已痴我已狂 我已疯我伪装
我已悲我已伤 我已扬
她是踏碎星河落入我梦境的幻想
环遍星系为你寻找的力量
神明给我在最难熬的时光
留下唯一的星光
堕入日月星辉之中梦的信仰
踏碎黎明星照映出的模样
铭憬银河最闪耀的地方
眷恋唯一的星光就是你

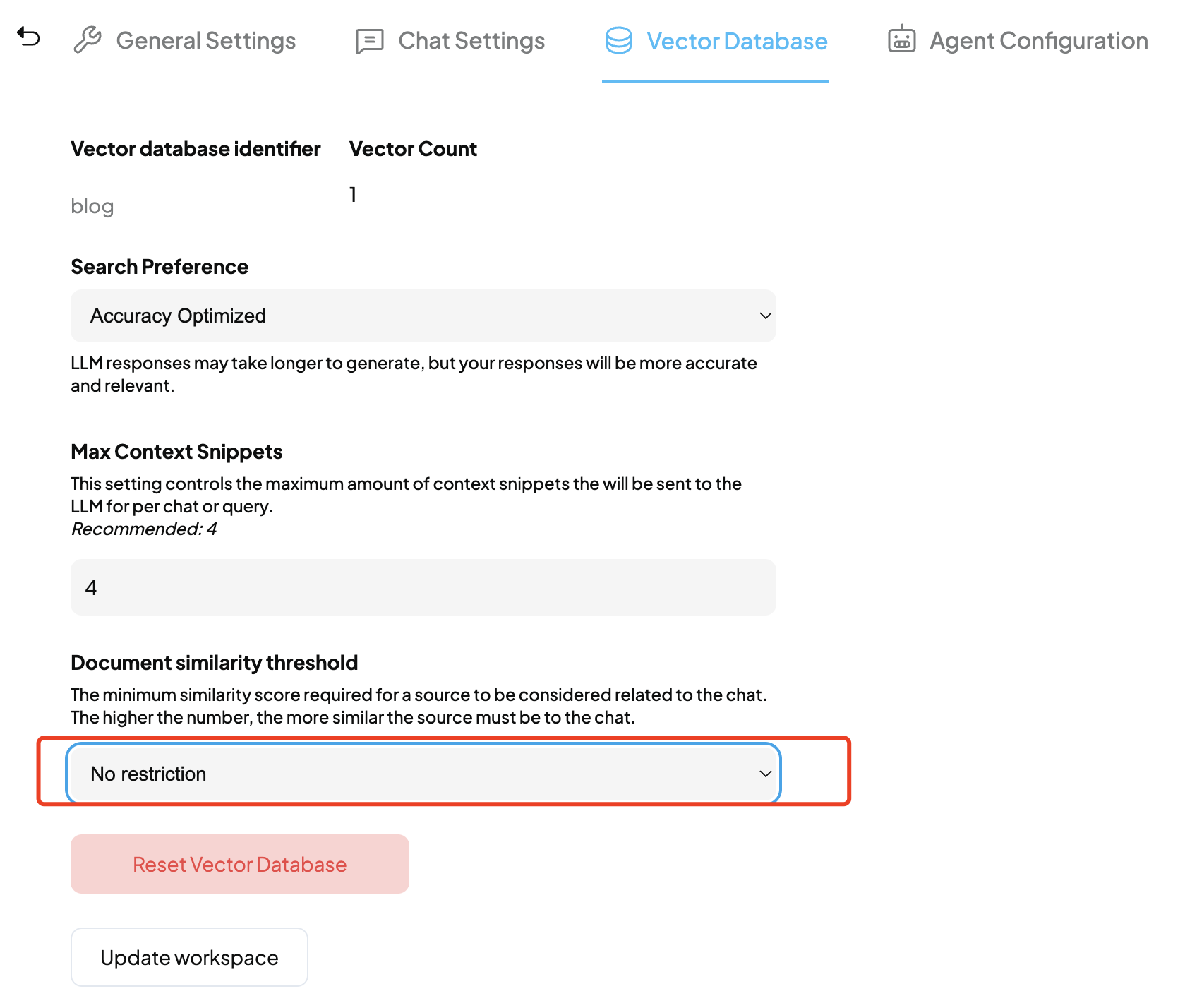
付公主的背包，用 \(ln\) 将卷积转为加法的 trick，link。

对于一个体积为 \(V\) 的物品，直接构建生成函数 \(A(x) = \sum\limits_{i=0}^{\infty}[i\bmod V=0]x^i\)，那么最后答案显然为所有的生成函数卷积，但是这样复杂度就是 \(O(nm\log n)\) 的，无法接受。

考虑一个生成函数的封闭形式，对于一个体积为 \(V\) 的物品，显然其生成函数 \(A(x)=\frac{1}{1-x^V}\)。考虑将乘法变成指数上的加减，即取 \(ln\)，但是不是对整个式子取 \(ln\)，而是分母 \(1-x^V\)。

因为这个式子取 \(ln\) 非常特殊，具体的，\(ln(1-x^V)=-\sum\limits_{i\ge 1}\frac{x^{Vi}}{i}\)。

证明

设 \(F(x)=1-x^V\)。

\[\begin{aligned}ln(F(x))&=G(x)\\\frac{F^{\prime}(x)}{F(x)}&=G^{\prime}(x)\quad(\text{两边同时求导，左侧链式法则})\\\frac{-Vx^{V-1}}{1-x^V}&=G^{\prime}(x)\\-\sum_{i\ge 0}Vx^{V-1+Vi}&=G^{\prime}(x)\quad(\text{将左边看成 $a\times \frac{1}{1-x^V}$})\\-\sum_{i\ge 0}\frac{Vx^{V+Vi}}{V+Vi}&=G(x)\\-\sum_{i\ge 1}\frac{x^{Vi}}{i}&=G(x) \end{aligned}\]

然后就是多项式 \(ln\)，经典调和级数将系数相加，然后求 \(exp\)，最后求逆即可，AC Link。

拓展题：P3784 [SDOI2017] 遗忘的集合（我还没写）

p