Float Double 浮点数 IEEE754 二进制表示法

news/2025/2/15 8:54:59/文章来源:https://www.cnblogs.com/zhangyukof/p/18716493

转载请标明原文地址:https://segmentfault.com/a/1190000041768195

Float二进制表示法

IEEE754标准中规定，单精度浮点数float占4字节32位
Sign(符号1位)|Exponent(指数8位 偏移127)|Mantissa(尾数23位)

Sign(符号)：表示浮点数的正负(大于等于0为0，小于0为1)
Exponent(指数)：表示浮点数的指数(类似科学计数法的指数部分)
Mantissa(尾数)：表示有效数字(类似科学计数法的有效数字)
以下内容简称这3部分分别为S、E、M

S、E、M 这3部分是怎么确定的呢？

比如11.25 表示成十进制的科学计数法: 1.125x101
符号是+，指数是1，有效数字是1.125

IEEE754是先把小数转成二进制，用二进制的科学计数法表示该小数。
还是以11.25为例:
S为0 (因为11.25不为负数)
把浮点数的整数部分和小数部分分别转成二进制，再拼到一起。

整数部分转二进制：

整数部分I为11，转成二进制为:1011
转换方法：整数除以2取余 余数倒序排列(除到整数部分为0)

11 ÷ 2 = 5 ··· 15 ÷ 2 = 2 ··· 12 ÷ 2 = 1 ··· 01 ÷ 2 = 0 ··· 1

小数部分转二进制：

小数部分F为0.25，转成二进制为:.01
转换方法：小数乘以2取整 整数正序排列(乘到小数部分为0，即余数为0)

0.25 x 2 = 0 ··· 0.5
0.5  x 2 = 1 ··· 0

整数和小数拼到一起：

IF = 1011.01

以二进制科学计数法表达：

IF = 1.01101x23

指数部分E：

E = 3， IEEE754规定这个值要加偏移值127
E = 3 + 127 = 130 转成二进制为:10000010
转换方法：整数除以2取余 余数倒序排列(除到整数部分为0)

130 ÷ 2 = 65 ··· 0 65 ÷ 2 = 32 ··· 132 ÷ 2 = 16 ··· 016 ÷ 2 =  8 ··· 08 ÷ 2 =  4 ··· 04 ÷ 2 =  2 ··· 02 ÷ 2 =  1 ··· 01 ÷ 2 =  0 ··· 1

尾数部分M：

M = 101101
由于二进制的科学计数法首位一定为1, 1可以省略不写，尾数部分就变成了01101
M = 01101

S、E、M三部分拼到一起：

0 | 10000010 | 01101 (后面补0够23位)
0 | 10000010 | 0110100 00000000 00000000

11.25转成float二进制最终结果就是：
0 10000010 0110100 00000000 00000000
用《在线浮点数转换工具》验证一下，结果正确。
float_11.25

二进制转Float

二进制11000000110110000000000000000000转Float怎么转呢?

还是先把二进制分为S、E、M三部分，分别转换后计算最终结果。

S(1位)|E(8位)|M(23位) 即
1 | 10000001 | 1011000 00000000 00000000
符号S: 1(值大于等于0时 S为0 值小于0时 S为1)
指数E：10000001
尾数M：1011000 00000000 00000000

指数E转整数：

E = 1000 0001 转整数
转换方法：从低位到高位 按位转成10进制相加

1x2⁷ + 0x2⁶ + 0x2⁵ + 0x2⁴ + 0x2³ + 0x2² + 0x2¹ + 1x2⁰ =
128  + 0    + 0    + 0    + 0    + 0    + 0    + 1    = 129

减去127(转二进制之前加了指数偏移量127 还原时需要减回来)
E = 129 - 127 = 2

尾数M转小数:

M = 1011
首位补1(为了节省空间 转换时去掉了首位的1 还原时需要补回来)
M = 11011
有效数字 科学计数法
M = 1.1011 x 22
M = 110.11
整数部分 I = 110 小数部分 F = .11

整数部分I转10进制:

I = 110 转成10进制为:6

1x2² + 1x2¹ + 0x2⁰ =
4    + 2    + 0    = 6

I = 6

F = .11 转为float为0.75

1x(½)¹ + 1x(½)² =
1/2    + 1/4    =
0.5    + 0.25   = 0.75

整数和小数部分拼接到一起:
6 + 0.75 = 6.75

加上符号位:
S = 1 (负数 符号为-)
float = -6.75

11000000110110000000000000000000 转成十进制最终结果就是 -6.75
用《在线浮点数转换工具》验证一下，结果正确。
float__6.75

Float特殊值

IEEE754规定了3个特殊值NaN、Infinity、-Infinity
分别代表:非数字(Not a number)、正无穷、负无穷
这个三个特殊值在转换时需要特殊处理

特殊值转换规则：

当指数E全部为1时为特殊值

1.尾数M全部为0

(1)符号位S为0时 值为正无穷Infinity

float_Infinity

(2)符号位S为1时 值为负无穷-Infinity

2.尾数M不全部为0

不管符号位S是0还是1 值均为NaN

float_NaN

float_NaN_2

Float序列化代码

private byte[] bytes = new byte[4];// float转字节数组
private void WriteFloat(float value) {int v = 0;unsafe { v = *(int*)&value; }bytes[0] = (byte)v;bytes[1] = (byte)(v >> 8);bytes[2] = (byte)(v >> 16);bytes[3] = (byte)(v >> 24);
}// 从字节数组中读取float
private float ReadFloat() {uint v = (uint)(bytes[0] | bytes[1] << 8 | bytes[2] << 16 | bytes[3] << 24);float value = float.NaN;unsafe { value = *(float*)&v; }return value;
}private void Test() {WriteFloat(1.23f);float v = ReadFloat();Trace.WriteLine(v);
}

Double二进制表示法

IEEE754标准中规定，双精度浮点数double占8字节64位
S、E、M三部分分别为:
S(1位)|E(11位 偏移1023)|M(52位)

以9.625为例：

S = 0 (正数)

整数部分转二进制：

整数部分 I = 9 转二进制为:1001
转换方法：整数除以2取余 余数倒序排列(除到整数部分为0)

 9 ÷ 2 = 4 ··· 1 4 ÷ 2 = 2 ··· 02 ÷ 2 = 1 ··· 01 ÷ 2 = 0 ··· 1

小数部分转二进制：

小数部分F为0.625，转成二进制为:.101
转换方法：小数乘以2取整 整数正序排列(乘到小数部分为0，即余数为0)

 0.625 x 2 = 1 ··· 0.250.25  x 2 = 0 ··· 0.50.5   x 2 = 1 ··· 0

整数和小数拼到一起：

IF = 1001.101

以二进制科学计数法表达：

IF = 1.001101 x 23

指数部分E：

E = 3, 加上偏移值1023
E = 1026 转成二进制为:10000000 010

转换方法：整数除以2取余 余数倒序排列(除到整数部分为0)

1026 ÷ 2 = 513 ··· 0513 ÷ 2 = 256 ··· 1256 ÷ 2 = 128 ··· 0128 ÷ 2 =  64 ··· 064 ÷ 2 =  32 ··· 032 ÷ 2 =  16 ··· 016 ÷ 2 =   8 ··· 08 ÷ 2 =   4 ··· 04 ÷ 2 =   2 ··· 02 ÷ 2 =   1 ··· 01 ÷ 2 =   0 ··· 1

尾数部分M：

M = 1001101
由于二进制的科学计数法首位一定为1, 1可以省略不写，尾数部分就变成了001101
M = 001101

S、E、M三部分拼到一起：

S(1位)|E(11位 偏移1023)|M(52位)
0 | 10000000 010 | 0011010... (后面补0够52位)

9.625转成double二进制最终结果就是 0 10000000010 0011010···
用《在线浮点数转换工具》验证一下，结果正确。
double_9.625

二进制转Double

二进制110000000101100100010···转double怎么转呢?
还是先把二进制分为S、E、M三部分，分别转换后计算最终结果。

1 | 10000000101 | 100100010···
S = 1 是负数 符号为-
E = 10000000101
M = 100100010···

指数E转整数：

E = 1000 0000 101 转整数
转换方法为:从低位到高位 按位转成10进制相加

1x2¹⁰ + 0x2⁹ + 0x2⁸ + 0x2⁷ + 0x2⁶ + 0x2⁵ + 0x2⁴ + 0x2³ + 1x2² + 0x2¹ + 1x2⁰ =
1024  + 0    + 0    + 0    + 0    + 0    + 0    + 0    + 4    + 0    + 1    = 1029

减去1023(转二进制之前加了指数偏移值1023 还原时需要减回来)
E = 1029 - 1023 = 6

尾数M转小数:

M = 1001 0001
首位补1(为了节省空间 转换时去掉了首位的1 还原时需要补回来)
M = 1100 1000 1
有效数字 科学计数法
M = 1.10010001 x 26
M = 1100100.01
整数部分 I = 1100100 小数部分 F = .01

整数部分I转10进制:

I = 1100100 转成10进制为:100
转换方法为:从低位到高位 按位转成10进制相加

1x2⁶ + 1x2⁵ + 0x2⁴ + 0x2³ + 1x2² + 0x2¹ + 0x2⁰ =
64   + 32   + 0    + 0    + 4    + 0    + 0    = 100

I = 100

小数部分F转10进制:
F = 01 转成10进制为：0.25

0x(½)¹ + 1x(½)² =
0      + 1/4    =
0      + 0.25    = 0.25

F = 0.25

整数和小数部分拼接到一起:
100 + 0.25 = 100.25

加上符号位:
S = 1 (负数 符号为-)
double = -100.25

二进制110000000101100100010··· 转成十进制最终结果就是 -100.25
用《在线浮点数转换工具》验证一下，结果正确。
double__1.0025e2

Double特殊值

IEEE754规定了3个特殊值NaN、Infinity、-Infinity
分别代表:非数字(Not a number)、正无穷、负无穷
这个三个特殊值在转换时需要特殊处理
double_特殊值

特殊值转换规则：

当指数E全部为1时为特殊值

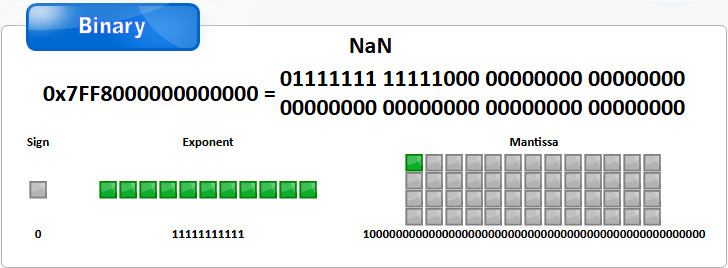
1.尾数M全部为0

(1)符号位S为0时 值为正无穷Infinity

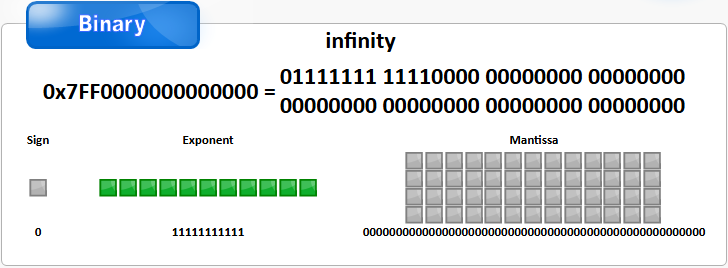
double_Infinity

(2)符号位S为1时 值为负无穷-Infinity

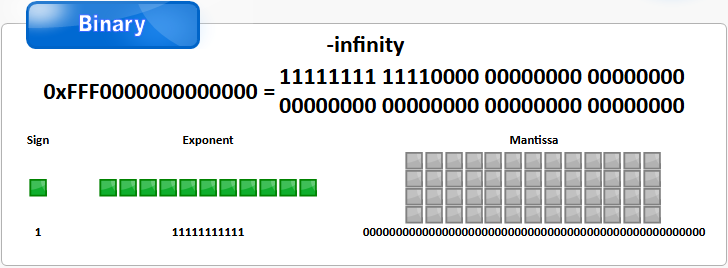
double__Infinity

1.尾数M不全部为0

不管符号位S是0还是1 值均为NaN

double_NaN

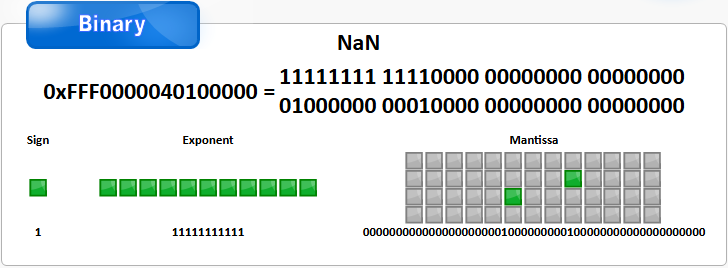
double_NaN_2

Double序列化代码

private byte[] bytes = new byte[8];private void WriteDouble(double value) {long v = 0;unsafe { v = *(long*)&value; }bytes[0] = (byte)v;bytes[1] = (byte)(v >> 8);bytes[2] = (byte)(v >> 16);bytes[3] = (byte)(v >> 24);bytes[4] = (byte)(v >> 32);bytes[5] = (byte)(v >> 40);bytes[6] = (byte)(v >> 48);bytes[7] = (byte)(v >> 56);
}public double ReadDouble() {int low = bytes[0] | bytes[1] << 8 | bytes[2] << 16 | bytes[3] << 24;int high = bytes[4] | bytes[5] << 8 | bytes[6] << 16 | bytes[7] << 24;long v = (uint)low | (long)high << 32;double value = double.NaN;unsafe { value = *(double*)&v; }return value;
}private void DoubleTest() {WriteDouble(-1.23456d);double v = ReadDouble();Trace.WriteLine(v);
}

总结：

Float转换规则

Sign(符号1位)|Exponent(指数8位 偏移值127)|Mantissa(尾数23位)

Double转换规则

Sign(符号1位)|Exponent(指数11位 偏移值1023)|Mantissa(尾数52位)

特殊值####

NaN、Infinity、-Infinity

if (指数E全部为1) {// 特殊值if (M == 0) {// 判断符号位if (S == 0) {// Infinity			} else {// -Infinity}} else {// NaN}
} else {// 正常值
}

IEEE754浮点数常见问题

1.有效数字位数限制

Float单精度浮点数大约6位有效数字
Double双精度浮点数大约15位有效数字
也就是说从左侧第一个不0的数字开始，Float能保证6位有效数字，再往后就不保证有效了
比如123.456f、0.123456f有效，12345.12345f(赋值后等于12345.123)、123456.1234f(赋值后等于123456.125)不能保证有效
Double能保证15位有效数字，再往后就不保证有效了
具体细节可以查看官方文档：C# 浮点数精度

2.尾数无限循环问题

由于浮点数转换为二进制时，某些数据比如0.1 小数部分乘2以后不能完全乘尽(0.2、0.4、0.8、0.6、0.2、0.4、0.8、0.6... 无限循环) 所以小数会出现丢失精度的情况，不能完全准确的表达这些乘不尽的情况，所以遇到类似精度丢失，数据变大了一点点，变小了一点点的问题，知道是这个原理导致的问题，既不是你写错了，也不是计算机出bug了，完全是转换规则的问题。float类型换成double提高精度依然会有该问题。想解决精度丢失的问题，可以把数字的小数部分当成整数计算 比如a=1.1 b=1.3 计算a+b 可以这样(Math.Round(a10) + Math.Round(b10)) / 10 注意数字别溢出最大范围

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/884126.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

五分钟搞定！Linux平台上用Ansible自动化部署SQL Server AlwaysOn集群

五分钟搞定！Linux平台上用Ansible自动化部署SQL Server AlwaysOn集群

五分钟搞定！Linux平台上用Ansible自动化部署SQL Server AlwaysOn集群前言 以下内容是由红帽官方博客整理而成，使用Ansible在Linux平台上自动化部署SQL Server AlwaysOn集群不熟悉整个流程的朋友可以先看之前的部署文章，手动部署一遍 从DNS配置到Pacemaker部署：一步步教你在…
阅读更多...
Wireshark的部署（学习笔记）

Wireshark的部署（学习笔记）

〇、大纲 1、远程数据包捕获 2、集线器环境下数据包捕获 3、交换机环境下数据包捕获 4、本地流量的捕获 5、虚拟机流量的捕获 一、远程数据包捕获 情形：需要异地管理分析服务器流量，有服务器控制权。方案：使用WinPcap下的Rpcap运行在目标服务器上，向远程控制机传回流量。服…
阅读更多...
递归总能够被彻底去除

递归总能够被彻底去除

阅读更多...
LeetCode 第24题：两两交换链表中的节点

LeetCode 第24题：两两交换链表中的节点

LeetCode 第24题：两两交换链表中的节点 题目描述 给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。 难度 中等 题目链接 https://leetcode.cn/problems/swap-nodes-in-pairs/ 示例 示…
阅读更多...
LeetCode 第25题：K 个一组翻转链表

LeetCode 第25题：K 个一组翻转链表

LeetCode 第25题：K 个一组翻转链表 题目描述 给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。 k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。 不能只是单纯的改变节点内部的值，…
阅读更多...
HJ25 数据分类处理

HJ25 数据分类处理

题目:我的答案: #include <iostream> #include <string> #include <vector> #include <set> #include <map>using namespace std;bool match(const int R, const string &I) {if (I.find(to_string(R)) != std::string::npos){return true;}…
阅读更多...
Java Web - 后端

Java Web - 后端

Java Web 后端的基础知识: Maven, Spring Boot, MySQL, JDBC, MyBatisJava Web - 后端 Maven 基于项目对象模型 (POM) 的概念, 通过一小段描述信息来管理项目的构建 官网各种插件以构建生命周期/阶段依赖管理模型从仓库中查找 jar包仓库: 存储资源, 管理 jar包本地仓库: 自己计…
阅读更多...
汇编语言笔记_1

汇编语言笔记_1

汇编语言学习笔记（一）1.基础知识 汇编语言是直接在硬件上工作的语言，本章重在了解硬件系统结构 1.1 机器语言 CPU（中央处理单元）是一种微处理器，功能是执行机器指令每一种微处理器由于硬件设计和内部结构的不同，有自己的机器指令集，也就是机器语言由于机器码晦涩难懂和…
阅读更多...
其他语法结构

其他语法结构

阅读更多...
基于FPGA的图像双线性插值算法verilog实现,包括tb测试文件和MATLAB辅助验证

基于FPGA的图像双线性插值算法verilog实现,包括tb测试文件和MATLAB辅助验证

1.算法运行效果图预览 (完整程序运行后无水印)这里实现的是256*256双线性插值到512*512的系统模块局部放大：将数据导入到matlab，得到插值效果图：2.算法运行软件版本 matlab2022avivado2019.23.部分核心程序 （完整版代码包含详细中文注释和操作步骤视频）`timescale 1ns / 1…
阅读更多...
Windows Teminal 自定义标题

Windows Teminal 自定义标题

背景与痛点场景： 开发环境，用命令行开了好几个微服务，窗口标题都是一样的，不好分清哪个窗口是哪个服务的了。所有窗口默认显示相同的标题（如"C:\Windows\System32\cmd.exe dotnet run"）。窗口多了，切换也不方便。 解决方案： 使用Windows Teminal 来运行命令启…
阅读更多...
前端开发day2

前端开发day2

前端开发day2 今日概要：案例应用（利用之前所学知识） CSS知识点 模板 + CSS + 构建页面1.CSS案例 1.1 内容回顾HTML标签 固定格式，记住标签长什么样子，例如： h/div/span/a/img/ul/li/table/input/formCSS样式引用CSS：标签、头部、文件 .xx{... }<div class=xx xx>&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023