B-树
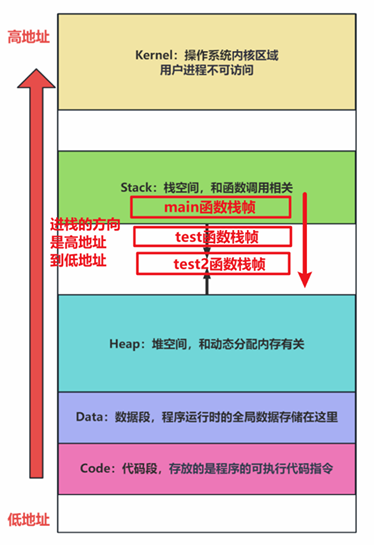
B-树(B树或B_树),这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树(B树是一颗多路平衡查找树)
它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。下图是 B-树的简化图。
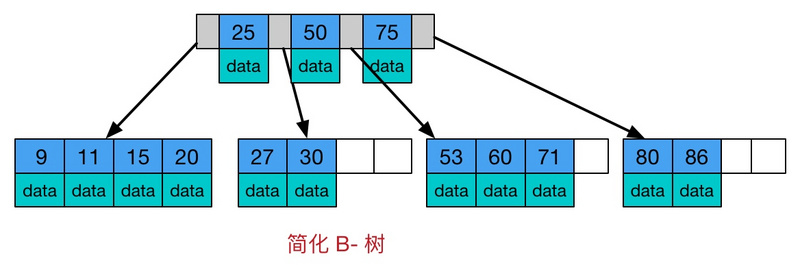
B-树有如下特点
- 所有键值分布在整颗树中(索引值和具体data都在每个节点里);
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束(最好情况O(1)就能找到数据);
- 在关键字全集内做一次查找,性能逼近二分查找;
B树由来
定义:B-树是一类树,包括B-树、B+树、B*树等,是一棵自平衡的搜索树,它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。
B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
定义只需要知道B-树允许每个节点有更多的子节点即可(多叉树)。子节点数量一般在上千,具体数量依赖外部存储器的特性。
先来看看为什么会出现B-树这类数据结构。
传统用来搜索的平衡二叉树有很多,如 AVL 树,红黑树等。这些树在一般情况下查询性能非常好,但当数据非常大的时候它们就无能为力了。原因当数据量非常大时,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能?减少磁盘 IO 次数,像 AVL 树,红黑树这类平衡二叉树从设计上无法“迎合”磁盘。
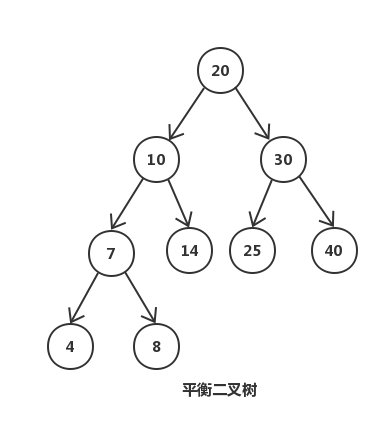
上图是一颗简单的平衡二叉树,平衡二叉树是通过旋转来保持平衡的,而旋转是对整棵树的操作,若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n(底数为2),这样逻辑上很近的节点实际可能非常远,无法很好的利用磁盘预读(局部性原理),所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。
空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问。
参考