【每日一题】20250216

【每日一题】

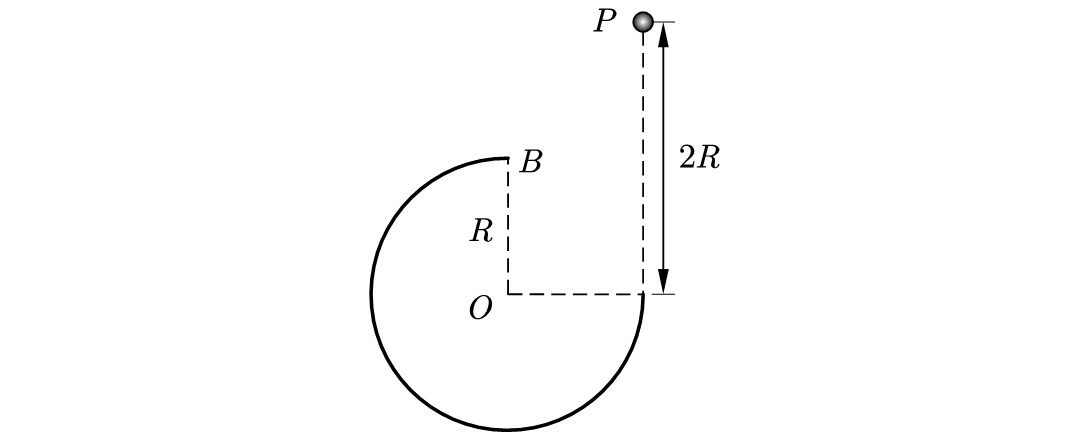
1. （多选）如图所示，在竖直半面内有一半径为 \(R\) 的圆弧轨道．半径 \(OA\) 木平、\(OB\) 竖直，一个质量为 \(m\) 的小球自 \(A\) 的正上方 \(P\) 点由静止开始自由下落，小球沿轨道到达最高点 \(B\) 时恰好对轨道设有压力．已知 \(AP=2R\)，重力加速度 \(g\)，则小球从 \(P\) 到 \(B\) 的运动过程中
   A. 重力做功 \(2mgR\)
   B. 机械能减少 \(mgR\)
   C. 合外力做功 \(mgR\)
   D. 克服摩擦力做功 \(\displaystyle \frac12mg R\)
   E. 若该圆弧轨道光滑，则小球在轨道最低端的压力最大
   F. 若该圆弧轨道光滑，则小球在轨道最低端的压力为 \(mg\)
   G. 若该圆弧轨道光滑，则小球可能无法到达轨道最高点
   

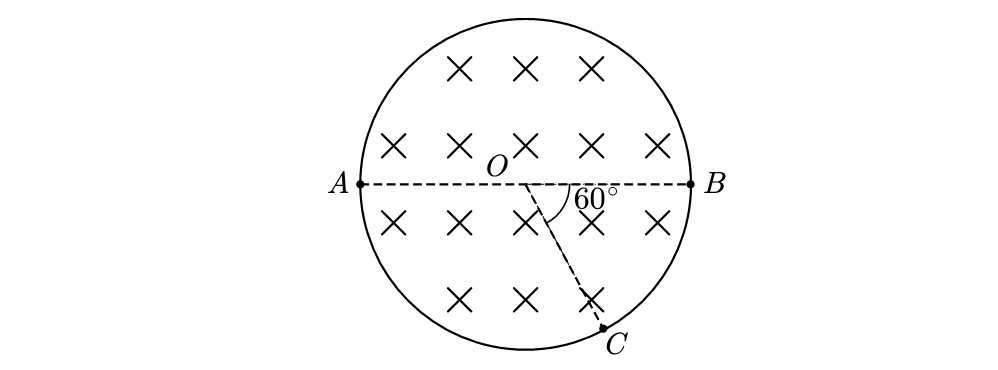
2. 如图所示，圆形区域内有垂直于纸面向里的匀强磁场，带电粒子以速度 \(v\) 从 \(A\) 点沿直径 \(AOB\) 方向射入磁场，经过 \(\Delta t\) 时间从 \(C\) 点射出磁场，\(OC\) 与 \(OB\) 成 \(60^{\circ}\)角。现将带电粒子的速度变为 \(\displaystyle \frac v3\)，仍从 \(A\) 点沿原方向射入磁场，不计重力，则粒子在磁场中的运动时间变为
   A. $\displaystyle \frac13 \Delta t $
   B. $\displaystyle \frac12 \Delta t $
   C. $2 \Delta t $
   D. $3 \Delta t $
   

[试题来源：]

---

【每日一言】

人生就是这样，不经历鲜血淋漓的疼痛，就不会明白那些曾经让我们厌烦的说教其实是受用一生的信条。 -《深海里的星星》独木舟

---

【学生撰写过程】

---

【答案】

---

未完待续~
2025-02-16 11:48:21 星期日