PyTorch 学习笔记：二分类神经网络实例

PyTorch 学习笔记：二分类神经网络实例

作者：BohengWebb

以下是菜鸟教程提供的一个二分类经典案例（有改动）：

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as pltn_samples = 100
data = torch.randn(n_samples, 2)
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()class SimpleNN(nn.Module): def __init__(self):super(SimpleNN, self).__init__()self.fc1 = nn.Linear(2, 4)self.fc2 = nn.Linear(4, 4)self.fc3 = nn.Linear(4, 1)self.sigmoid = nn.Sigmoid()def forward(self, x):x = torch.relu(self.fc1(x))x = torch.relu(self.fc2(x))x = self.sigmoid(self.fc3(x))return xmodel = SimpleNN()criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.05)epochs = 50000
for epoch in range(epochs):outputs = model(data)loss = criterion(outputs, labels)optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 10 == 0:print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')def plot_decision_boundary(model, data):x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)predictions = model(grid).detach().numpy().reshape(xx.shape)plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')plt.title("Decision Boundary")plt.show()plot_decision_boundary(model, data)

该案例主要分为五个大块：生成训练集，定义前馈神经网络，定义损失函数和优化器，训练，预测测试集。

写在前面

文件最开头引入了在该实例中需要用到的包：

import torch # 导入PyTorch模块
import torch.nn as nn #导入PyTorch.nn模块
import torch.optim as optim # 导入PyTorch中的optim模块
import matplotlib.pyplot as plt # 绘图工具Matplotlib

• import torch：导入PyTorch模块

• import torch.nn as nn：导入PyTorch.nn模块，以构建神经网络

• import torch.optim as optim ：导入PyTorch中的optim模块

  optim模块提供了各种优化算法，如SGD（随机梯度下降）、Adam等，这些优化算法用于在训练神经网络时更新网络的权重参数，以最小化损失函数

• import matplotlib.pyplot as plt ：导入绘图工具Matplotlib

以上是一些准备工作。

生成训练集

本实例中，生成训练集干了两件事：第一，随机生成训练集；第二，可视化样本点。

随机生成训练集

随机生成坐标存储在张量 data 中，再给这些坐标作上对应的标签（红/蓝）并存储在张量 lables 中。

n_samples = 100 # 设置随机数据的数量
data = torch.randn(n_samples, 2)  # 生成 100 个二维数据点
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)  # 点在圆内为1，圆外为0

• n_samples = 100：设置随机数据的数量为100个

• data = torch.randn(n_samples, 2) ：生成 100 个二维数据点

  这里运用torch.randn()方法创建了一个服从正态分布的随机张量data。这个张量中的数据均值为 0，标准差为 1，共有2列、100行（随机数据的数量）

下面这行代码比较重要。

labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)：这行代码的目的是为每个生成的二维数据点生成一个标签，用于表示该点是否位于单位圆内。点在圆内为1，圆外为0。

具体步骤如下：

• data[:, 0]**2 + data[:, 1]**2：计算每个数据点到原点的欧几里得距离的平方，即\(x_1^2 + x_2^2\)

  data[:, 0] 表示取 data 张量的第一列（即所有数据点的第一个特征值）

  data[:, 1] 表示取 data 张量的第二列（即所有数据点的第二个特征值）

• < 1：判断每个数据点的欧几里得距离平方是否小于1。如果小于1，则该点位于单位圆内，结果为True；否则位于单位圆外，结果为False

• .float()：将布尔值True和False转换为浮点数1.0和0.0，以便在后续的机器学习任务中使用

• .unsqueeze(1)：在第1维（Python中索引从0开始，所以这里的1实际上是第二维）增加一个维度，将标签的形状从(100,)变为(100, 1)

  这是因为在许多机器学习框架中，标签通常需要是一个二维张量，其中第二维表示标签的维度。在二分类问题中，这个维度通常为 1

  关于为什么最后要加上这个unsequeeze(1)，因为要遵从二分类问题处理的习惯。

  （其实到现在也不太理解为什么）

可视化样本点

plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm') # 绘制散点图plt.title("Generated Data") # 图表标题
plt.xlabel("Feature 1") # x轴的含义
plt.ylabel("Feature 2") # y轴的含义
plt.show() # 显示图表

这里比较重要的就是第一行代码：

plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm') ：用于绘制散点图

此处涉及到plt.scatter()方法的参数：plt.scatter(x坐标,y坐标,c=点的颜色,cmap=使用colormap的名字)

• c=labels.squeeze()：这个参数用于指定每个点的颜色

  由于labels 是一个二维张量，其中每个元素表示对应数据点的标签（0 或 1），所以就用squeeze() 来去除 labels 张量中维度为 1 的维度，使其变回一维张量（刚刚unsequeeze(1)人为加了一个维度，现在再还原回去）

  最终，c的取值要么0，要么1。这样，每个点的颜色就由其对应的标签决定。

• cmap='coolwarm'：这个参数用于指定颜色映射（colormap）

  coolwarm 是 Matplotlib 中的一个预定义颜色映射，它将数值映射到从蓝色到红色的颜色范围。在这个例子中，标签为 0 的点将被映射到蓝色，标签为 1 的点将被映射到红色。

  0蓝1红这个映射规则是由coolwarm这个库决定的

常用的colormap如下：

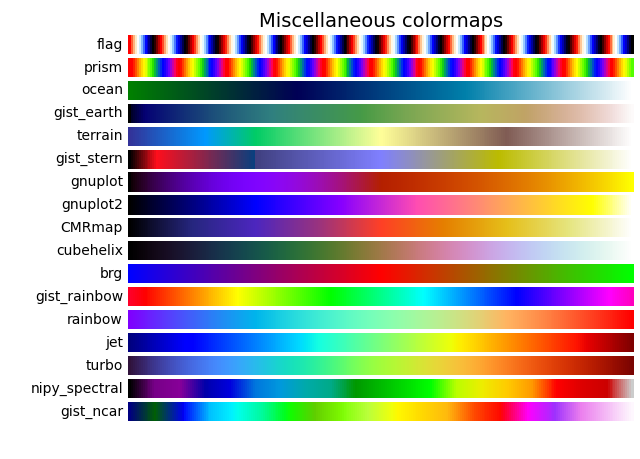
通过这一步，我们可以直观地查看到我们的样本点并生成图像。

定义前馈神经网络

定义前馈神经网络这一过程的代码大体分为两部分：定义神经网络的层；描述前向传播的过程。不过在编写定义前馈神经网络的代码之前，首先需要思考该如何设计这个神经网络，以达成我们所需要的二分类目标。

设计神经网络的层

我们前面提到，样本点都在一个圆内。在分类问题中，机器只会画直线、平面等简单几何图形，反映到代数层面就是——机器只能列出一个一次方程，机器只能确定方程中变量的参数。那么很显然，简单的几何图形——例如直线，无论如何都无法用一条直线将图形切成一边全红、一边全蓝的局面。但是，我们可以把图形投影到更高的维度，在更高的维度上进行拉伸和扭曲，从而用一个高维的面来切开两类样本点。

这里所说的拉伸，是指定义矩阵 \(\mathbf W_{fcx}\) 与向量 \(\mathbf b_{fcx}\) ，使得数据组可以进行线性变换以及位移；这里所说的扭曲，是指利用预定义的一系列激活函数（这类函数通常是非线性的）来把空间扭曲，继而分出相应的点。人工智能中所说的“学习”，很大程度上指的是运用反复的训练与纠错，得到最接近完美答案的矩阵 \(\mathbf W_{fcx}\) 与向量 \(\mathbf b_{fcx}\)。

常用的激活函数有：阶跃函数（Step Function）、ReLU（线性整流函数）、\(\sigma\)（Sigmoid函数）、tanh（双曲正切函数）、softmax 函数。softmax 函数通常用于多分类问题最后的输出。

\[s(x)=\begin{cases}0 & ,x<0\\1 & ,x\geq0 \end{cases} \]

\[{\rm ReLU}(x)=\begin{cases}0 & ,x\leq0\\x & ,x>0 \end{cases} \]

\[\sigma(x)=\frac{1}{1+e^{-x}} \]

\[\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \]

\[{\rm softmax}(x_i)=\frac{e^{x_i/T}}{\displaystyle\sum_{n=0}^{N-1}e^{x_n/T}} \]

为了分开处于圆圈中的点，我们需要将二维的平面经过矩阵乘法升维到更高的维度（如三维空间、四维空间……），然后在高维空间中利用激活函数将平面的中心坍缩下陷，于是我们就可以进行切割、继而分类了。

第一个过程（fc1）

经测试，升维到三维固然可以区分开，但不够稳定，故此处我们考虑升到四维。

升到四维后，我们采用 ReLU 作为激活函数。ReLU 函数的优点是，它的输出范围较大，不像 Sigmoid 会大幅压缩值域；并且 ReLU 函数不涉及到指数函数，这对后续的梯度下降可以降低算力成本，更有利于机器进行学习。有趣的是，有一种说法认为，基于 ReLU 函数运算过程——以0为阈值，低于0处于“未激活”，不允许通过，高于0则被“激活”，允许放行——这一过程更加贴近自然界生物神经元处理、传导电信号的过程。

我们可以将第一个过程 fc1 用公式表示为：

\[\mathbf a^{(1)}={\rm ReLU}(\mathbf W_{fc1} \mathbf a^{(0)}+\mathbf b_{fc1}) \]

公式中的 \({\rm ReLU()}\) 表示的是对向量中的每一个数取 ReLU 函数。

fc1 过程完成了从输入层（第一层）到第一个隐藏层（第二层）的映射。

第二个过程（fc2）

为了保证结果被区分得更细，我们选择再加一层，以提高正确率。但是，如果维数被升得太高、层数被涉及太多，可能会出现过拟合的问题。在这里，第二个过程其实是一个从四维到四维的过程，并没有维数的改变，仅仅是一个线性变换。

我们可以将第二个过程 fc2 用公式表示为：

\[\mathbf a^{(2)}={\rm ReLU}(\mathbf W_{fc2} \mathbf a^{(1)}+\mathbf b_{fc2}) \]

fc2 过程完成了从第一个隐藏层（第二层）到第二个隐藏层（第三层）的映射。

第三个过程（fc3）

最后，我们将结果降回一维，得到最终的结果。如果结果接近0，这个数据点就是蓝色阵营，如果结果接近1，这个数据点就是红色阵营。由此作出结论，从而达到利用模型预测的目的。

这里，我们使用 Sigmoid 函数，这是因为我们要把结果限定在一个范围之内。

我们可以将第三个过程 fc3 用公式表示为：

\[\mathbf x=\sigma(\mathbf W_{fc3} \mathbf a^{(2)}+\mathbf b_{fc3}) \]

fc3 过程完成了从第二个隐藏层（第三层）到输出层（第四层）的映射。

我们可以将我们设计出来的神经网络表示为下图。

定义神经网络的层

先说一下下面这一行：

class SimpleNN(nn.Module): 

这一行代码定义了一个类，这个类名字叫SimpleNN，而后面的“参数”表示的是类的继承。继承，意味着子类会继承父类中的属性与方法

SimpleNN作为子类是继承自nn.Module这个父类的；nn.Module是torch.nn中自带的一个类。

在PyTorch中，构建神经网络通常需要继承nn.Module类，nn.Module是所有神经网络模块的基类，你需要定义以下两个部分：

• __init__()：定义网络层

• forward()：定义数据的前向传播过程

	def __init__(self):super(SimpleNN, self).__init__()# 定义神经网络的层self.fc1 = nn.Linear(2, 4)  # 输入层有 2 个神经元（x，y），隐藏层有 4 个神经元self.fc2 = nn.Linear(4, 4)self.fc3 = nn.Linear(4, 1)  # 隐藏层输出到 1 个神经元（用于二分类）self.sigmoid = nn.Sigmoid()  # 二分类激活函数

def __init__(self):开始定义网络层

• __init__()是一个特殊方法，称为构造方法，在实例化以后，会自动调用__init__()方法。
• Python中类里的所有方法必须有一个额外的“第一个参数”名称, 按照惯例它的名称是self

super(SimpleNN, self).__init__()调用父类 nn.Module 的构造函数，确保子类 SimpleNN 能够正确地继承父类的属性和方法

• 在 Python 中，当你定义一个子类并希望在子类的构造函数中调用父类的构造函数时，可以使用 super() 函数

• super() 函数用于调用父类的方法，这里是调用父类nn.Module的构造函数

  在这个例子中，SimpleNN 是一个自定义的神经网络类，它继承自 nn.Module，通过调用 super(SimpleNN, self).__init__()，SimpleNN 类可以继承 nn.Module 的属性和方法

self.fc1 = nn.Linear(2, 4)设置线性层间关系，后面以此类推

• 这一行表示的是对于我这个结构体的fc1变量（一个参量），设置为一个线性的层间关系
• Linear表示的是“从A到B”的“到”，描述层与层中间的过程，这里是连接了从2个神经元到4个神经元的过程，做的是“连线”工作

self.sigmoid = nn.Sigmoid() 使用 Sigmoid 函数进行训练

描述前向传播的过程

	def forward(self, x):x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数x = torch.relu(self.fc2(x))x = self.sigmoid(self.fc3(x))  # 输出层使用 Sigmoid 激活函数return x

def forward(self, x):开始描述前向传播的过程。这里丢入了一个参数x，x就是我传入的样本数据或训练数据

x = torch.relu(self.fc1(x))表示使用 ReLU 函数。

关于为什么这里不用写self.x=：写self.x=只是在写入一个内参的数据，这个参数的作用域仅在这个函数内；写x=就是为了处理我的数据，即“输入层神经元”的张量

这里其实就说明了定义前向传播的过程：

1. 先获取x，丢入fc1过程，然后经历ReLU，把结果更新到x
2. 再获取x，丢入fc2过程，然后经历ReLU，把结果更新到x
3. 再获取x，丢入fc3过程，然后经历Sigmoid，把结果更新到x
4. 返回最终的x

参数x其实就是在跟踪并实时更新当前“运行到的”层中的所有数据.

实例化

# 实例化模型
model = SimpleNN()

最终，我们把神经网络进行实例化。这个实例的名字叫做 model。

我们上面写的“类”，相当于是画了一张名字叫SimpleNN()的图纸。这张图纸上清晰地展示了，通过SimpleNN()图纸造出来的神经网络，应该长什么样。但是，图纸本身不能作为一个模型去预测数据，根据图纸“造”出来的东西才能干这些事。打一个比方，对于房屋图纸，画了屋子的图纸本身不能住人，根据图纸造出来的屋子才能住人。

实例化的过程就是“造”东西，我们根据SimpleNN()图纸，“造”出来了model模型。这个model模型才是之后帮助我们预测数据的东西。

定义损失函数和优化器

# 定义损失函数和优化器
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.05)  # 使用随机梯度下降优化器

损失函数用于衡量模型的预测值与真实值之间的差异。常见的损失函数包括：

• 均方误差损失（MSELoss）：回归问题常用，计算输出与目标值的平方差。

  使用方法：criterion = nn.MSELoss()

• 交叉熵损失（CrossEntropyLoss）：分类问题常用，计算输出和真实标签之间的交叉熵。

  使用方法：criterion = nn.CrossEntropyLoss()

• BCEWithLogitsLoss：二分类问题，结合了 Sigmoid 激活和二元交叉熵损失。

  使用方法：criterion = nn.BCEWithLogitsLoss()

经测试，在本案例中，使用 BCELoss 作为损失函数时，梯度下降的速度比 MSELoss 作为损失函数时更快。

优化器负责在训练过程中更新网络的权重和偏置。常见的优化器包括：

• SGD（随机梯度下降）

  使用方法：optimizer = optim.SGD(model.parameters(), lr=0.01)

• Adam（自适应矩估计）

  使用方法：optimizer = optim.Adam(model.parameters(), lr=0.001)

• RMSprop（均方根传播）

这里的lr表示学习率，是一个人为预设的值，表示每次更新的步长。在本实例中，我们设置为0.05。

学习率的存在可以防止出现锁死局部最低点的情况。学习率会最终成为一个比例乘给梯度。

训练

在开始训练前，我们设置了训练的轮数：

epochs = 50000 # 设置训练轮数
for epoch in range(epochs):

这里的“训练”，指的是把训练集丢入模型内，将整个训练集遍历1次即为“1轮”。通常情况下，训练的轮数越高，模型的预测值与真实值之间的差异就越低，相应地就能提高预测的准确性。（这里暂不讨论过拟合的情况）

经测试，当训练轮数达到 5000 轮时，模型能初步划分出红蓝区域；当训练轮数达到 10000 轮时，模型划分区域的准确率较为可观；随后，模型的准确率缓慢上升；当训练轮数达到 50000 轮时，模型的准确率通常已经可以达到 99.90% 以上。

这里，我们设置训练轮数为 50000 轮。随后将“1轮”训练的过程写在 for 循环中，循环 50000 次。

for 循环内就是训练的主体过程。训练的主体过程分为两个大块：前向传播与反向传播。

前向传播

    # 前向传播outputs = model(data)loss = criterion(outputs, labels)

• outputs = model(data)：把所有数据丢进去，得到计算结果。

  这里的 data 就是刚刚的参数 x，模型最后算出来的结果最终返回给 outputs 对象。

• loss = criterion(outputs, labels)：把计算结果（预测值，存储在outputs中）、正确结果（真实值，存储在lables中）丢入损失函数，计算出损失（也就是错误率）。

前向传播，可以理解为“向前算”。从输入层开始，一步步算出我当前模型的计算结果，然后“核对答案”，算出“错误率”（也就是损失函数）。

反向传播

    # 反向传播optimizer.zero_grad()  # 梯度清零loss.backward()  # 反向传播计算梯度optimizer.step()  # 更新参数

• optimizer.zero_grad()：用于将模型参数的梯度清零。

  在每次进行反向传播之前，需要将之前计算的梯度清零，以避免梯度累加。

  这是因为在 PyTorch 中，梯度是累加的，即每次调用 backward() 方法时，梯度会被累加到之前的梯度上。因此，在每次迭代开始时，需要将梯度清零，以确保每次计算的梯度是当前批次数据的梯度。

• loss.backward()：用于执行反向传播，计算损失函数关于模型参数的梯度。

  backward() 方法会自动计算损失函数关于模型参数的梯度，并将这些梯度存储在模型参数的 .grad 属性中。

• optimizer.step()：用于根据计算得到的梯度更新模型参数。

  step() 方法会根据优化器的更新规则（例如学习率、动量等），根据计算得到的梯度更新模型的参数。

反向传播，可以理解为“向后算”。从输出层开始，一步步根据损失函数来修正模型、优化模型，算出优化后的模型内参数（也就是前文提到的矩阵 \(\mathbf W_{fcx}\) 与向量 \(\mathbf b_{fcx}\)）。

最后，为了让我们能直观地看出当前训练的状态，我们设定每 10 轮打印一次损失。

    # 每 10 轮打印一次损失if (epoch + 1) % 10 == 0:print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

关于这里的 epoch + 1：这是因为 for 循环中的 range() 函数是从 0 开始数数的，当 epoch 为 0 时，实际上当前的轮数为第 1 轮。所以，我们要将 epoch 加上 1。

通过这一步，我们可以直观地看出当前训练的状态。在下图所示的训练过程中，模型的最终准确率达到了 99.93%。

预测测试集

接下来这一部分菜鸟教程提供的源代码其实是在一边画图一边预测数据。大体思路如下：

1. 在一个网格图中每隔一个很小的段取一个点，最后取出很多点。这些点在图像上呈现为点阵。
2. 把这些点打包为一个张量，直接把这个张量充当测试集使用。
3. 把这些测试集丢入模型当中，计算（预测）出其中的每一个点属于红色阵营还是蓝色阵营，达到分类的目的。
4. 绘制等高线图，区分出红色阵营与蓝色阵营。
5. 将红蓝分界线作为决策边界，输出图像。

上面这一整个过程都被封装在函数plot_decision_boundary(model, data)中。

• model：训练好的模型；
• data：用于训练的数据集。

生成训练集

def plot_decision_boundary(model, data): x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1# 生成网格xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), torch.arange(y_min, y_max, 0.1), indexing='ij')grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)

前两行主要是为了找到图像的最终边界：

• Line1：计算数据集中第一个特征（即 data 张量的第一列）的最小值和最大值，并分别减去和加上 1，确保决策边界能够覆盖整个数据集；

• Line2：计算数据集中第二个特征（即 data 张量的第二列）的最小值和最大值，并分别减去和加上 1，确保决策边界能够覆盖整个数据集。

接下来开始生成网格，同时也是生成测试集。

xx 是网格的 x 坐标，yy 是网格的 y 坐标。我们使用 torch.meshgrid 函数生成一个二维网格。生成这个网格是为了定坐标点，然后描点勾线画图。

torch.meshgrid 函数的参数含义如下：

• torch.arange(x_min, x_max, 0.1)：生成从 x_min 到 x_max 的等间隔序列，间隔为 0.1。
• torch.arange(y_min, y_max, 0.1)：生成从 y_min 到 y_max 的等间隔序列，间隔为 0.1。
• indexing='ij'：使用矩阵索引方式。

grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)：将 xx 和 yy 张量展平并拼接成一个二维张量 grid，其中每一行表示一个网格点的坐标。

• xx.reshape(-1, 1) 将 xx 张量展平为一列，yy.reshape(-1, 1) 将 yy 张量展平为一列；
• 然后使用 torch.cat 函数在第二维（即列）上拼接这两个张量。
• 最终，grid呈现为一个一个二维点构成的集合。

稍后，grid中的全部点将作为测试集（不同于训练集），丢入模型

利用模型预测

    # 利用模型预测predictions = model(grid).detach().numpy().reshape(xx.shape)

• model(grid)：将网格点的坐标 grid 输入到神经网络模型中，得到模型对每个网格点的预测结果。

• .detach().numpy()：将预测结果从 PyTorch 张量转换为 NumPy 数组，并从计算图中分离出来，以避免梯度计算。

  （为什么要避免梯度计算？）

• .reshape(xx.shape)：将预测结果的形状调整为与 xx 张量的形状相同，以便后续绘制等高线图。

叠加绘制等高线图、散点图

    plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')plt.title("Decision Boundary") # 设置图表的标题为 "Decision Boundary"。plt.show() # 显示图表。

使用 plt.contourf 函数绘制等高线图：

• xx 和 yy：网格点的坐标
• predictions：模型对每个网格点的预测结果。
• levels=[0, 0.5, 1]：等高线的级别，
• cmap='coolwarm'：使用 coolwarm 颜色映射，
• alpha=0.7：透明度为 0.7，好看一点。

关于什么是等高线的级别：等高线的级别决定了等高线图中不同颜色区域的边界。

具体来说：

• 0 表示第一个级别，通常对应于数据中的最小值或某个特定的阈值。在这个例子中，0 可能表示模型预测为负类（例如，标签为 0）的区域。
• 0.5 表示第二个级别，通常对应于数据中的中间值或某个特定的阈值。在这个例子中，0.5 可能表示模型预测为不确定或边界区域的区域。
• 1 表示第三个级别，通常对应于数据中的最大值或某个特定的阈值。在这个例子中，1 可能表示模型预测为正类（例如，标签为 1）的区域。

通过指定这些级别，plt.contourf 函数会根据模型的预测结果在不同的区域填充不同的颜色，从而直观地展示模型的决策边界。

使用 plt.scatter 函数绘制原始数据点的散点图：

• data[:, 0] 和 data[:, 1]：数据点的坐标，
• c=labels.squeeze()：使用数据点的标签作为颜色，
• cmap='coolwarm'：使用 coolwarm 颜色映射，
• edgecolors='k'：数据点的边缘颜色为黑色。

这一步和最初画训练点集的代码差不多

输出图像

# 输出图像
plot_decision_boundary(model, data)

通过这一步，我们可以直观地看出最后模型的预测结果并生成图像。