数据结构选讲-1 总结

数据结构选讲-1 总结

线段树技巧及其应用。

前言

出题特点：

• 树形 \(polylog\) 数据结构为主，尤其线段树。
• 侧重数据结构维护算法，使用数据结构进行统计。
• 强调“从具体情境中抽象出合适的数据及目标”的过程。

数据结构本质上是要在数据和目标不变的情况下，优化算法复杂度，降低程序时间开销。

“从计算层面优化算法复杂度”问题的特点：

情境复杂，没有First Principle。

导致这样的实际情况：

• 需要细致地分析问题，找出题目的特殊之处，分析独有的性质。
• “见多识广”、积累技巧可能有用。
• 既要充分调动经验，又忌轻易套用模型或经验。

优化程序时间开销的一般思想：

• 分组处理：几乎一切数据结构（包括分块、倍增），二进制分组等。
• 减小计算量：记忆化，标记，采样；“支配”性质。
• 调度计算顺序：分治法，调换维度，预处理。
• 激发硬件性能：并行计算（压位、bitset）。

如何优雅地写出300行代码？

• think twice, code once.

  在实现之前推敲各类讨论和关键细节，在实现过程中集中注意力，清楚正在实现部分的功能。

• 在关键的地方留一些注释。

• 按照一定的顺序编写代码。

  打框架->实现简单（模板化）的辅助数据结构->实现复杂（根据题目特殊调整）的数据结构。

  框架限制了你实现数据结构时的奇思妙想，模板化的数据结构为效率服务，复杂数据结构以模板为基础构建减少出错概率。

• 每个函数的副作用尽量小，避免出现莫名其妙的相互作用（i.e. 少用全局 变量）；数据结构最好可以做好封装。

• 注意清空！注意清空！注意清空！

• 可以有意识地积累错误和错因，避免犯第二次错。

• 训练时不要复制数据结构模板，训练多写，考试少调。

• debug 时看注释对思路，分步分阶段调试，多思考实现方式，找清代码错误，减少调试时间。

线段树常见技术

• zkw
• 历史信息
• 线段树二分
• 势能线段树
• 可持久化线段树
• 线段树合并分裂

Warm up!

彩虹蛋糕

将 \(\max\) 拆成两个不等式 \(a_c-a_y<b_y-b_c\) 与 \(a_c-a_y>b_y-b_c\)。

将其作为下标插入到线段树中，利用线段树本身的偏序关系，维护该区间的最值。

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define pii pair<ll,ll>
#define fi first
#define se second
#define inf 1e18const int maxn=1e6+5,N=2e6;int q;
int OP1[maxn],OP2[maxn],X[maxn],Y[maxn];map<int,int>mp;namespace linetree
{#define lch(p) p*2#define rch(p) p*2+1struct treenode{pii U,V;multiset<int>P1,P2;ll mn;}tr[maxn*8];inline void pushup(int p){tr[p].U.fi=min(tr[lch(p)].U.fi,tr[rch(p)].U.fi);tr[p].V.fi=min(tr[lch(p)].V.fi,tr[rch(p)].V.fi);tr[p].U.se=min(tr[lch(p)].U.se,tr[rch(p)].U.se);tr[p].V.se=min(tr[lch(p)].V.se,tr[rch(p)].V.se);tr[p].mn=min({tr[lch(p)].mn,tr[rch(p)].mn,(ll)tr[lch(p)].U.se+tr[rch(p)].V.se,(ll)tr[lch(p)].V.fi+tr[rch(p)].U.fi});}inline void build(int p,int l,int r){if(l==r){tr[p].mn=inf;tr[p].U=tr[p].V={inf,inf};return ;}int mid=(l+r)>>1;build(lch(p),l,mid);build(rch(p),mid+1,r);pushup(p);}inline void insert(int p,int l,int r,int typ,int pos,int x,int y){if(l==r){if(typ==1){tr[p].P1.insert(y);tr[p].U.se=*tr[p].P1.begin();tr[p].U.fi=tr[p].U.se+x;}else{tr[p].P2.insert(y);tr[p].V.se=*tr[p].P2.begin();tr[p].V.fi=tr[p].V.se-x;}tr[p].mn=max(tr[p].V.fi+tr[p].U.fi,tr[p].U.se+tr[p].V.se);return ;}int mid=(l+r)>>1;if(pos<=mid) insert(lch(p),l,mid,typ,pos,x,y);else insert(rch(p),mid+1,r,typ,pos,x,y);pushup(p);}inline void det(int p,int l,int r,int typ,int pos,int x,int y){if(l==r){if(typ==1){tr[p].P1.erase(tr[p].P1.lower_bound(y));if(tr[p].P1.empty()) tr[p].U={inf,inf};else {tr[p].U.se=*tr[p].P1.begin();tr[p].U.fi=tr[p].U.se+x;}}else{tr[p].P2.erase(tr[p].P2.lower_bound(y));if(tr[p].P2.empty()) tr[p].V={inf,inf};else {tr[p].V.se=*tr[p].P2.begin();tr[p].V.fi=tr[p].V.se-x;}}tr[p].mn=max(tr[p].V.fi+tr[p].U.fi,tr[p].U.se+tr[p].V.se);return ;}int mid=(l+r)>>1;if(pos<=mid) det(lch(p),l,mid,typ,pos,x,y);else det(rch(p),mid+1,r,typ,pos,x,y);pushup(p);}
}signed main()
{// freopen("set.in","r",stdin);// freopen("set.out","w",stdout);scanf("%d",&q);linetree::build(1,1,N);for(int i=1;i<=q;i++){scanf("%d%d%d%d",&OP1[i],&OP2[i],&X[i],&Y[i]);mp[X[i]-Y[i]]=1;mp[Y[i]-X[i]]=1;}auto it1=mp.begin(),it2=mp.begin();for(it2++;it2!=mp.end();it1++,it2++) it2->second+=it1->second;for(int i=1;i<=q;i++){int op1,op2,x,y;op1=OP1[i],op2=OP2[i],x=X[i],y=Y[i];if(op1==1) linetree::insert(1,1,N,op2,(op2==1)?mp[x-y]:mp[y-x],(op2==1)?x-y:y-x,y);else linetree::det(1,1,N,op2,(op2==1)?mp[x-y]:mp[y-x],(op2==1)?x-y:y-x,y);printf("%lld\n",linetree::tr[1].mn>=inf?-1:linetree::tr[1].mn);}
}

青蛙题/P7907 Ynoi2005 rmscne

枚举 \(r\)，对于每个 \(l\) 维护最小的 \(f_l\)，使得 \([l,f_l]=[l,r]\)。

易于发现，设 \(a_i\) 上次出现在 \(pos_i\)，需要将 \(l\in[pos_i+1,i]\) 的 \(f_l\) 改为 \(r\)。

同时对于起点 \(l\) 维护最大的 \(t_l\) 满足 \([t_l,r]=[l,r]\)。

用并查集，将 \(t_{pos_r}\) 连接至 \(t_{pos_r+1}\)，表示 \(t_{pos_r}\) 消除 \(pos_r\) 的局限，可以向后移动至 \(t_{pos_r}\) 所在位置。

#include<bits/stdc++.h>
using namespace std;const int maxn=2e6+5;int n,q;
int a[maxn],pre[maxn],nxt[maxn],lst[maxn],lg[maxn],l[maxn],r[maxn],ans[maxn];vector<int>vec[maxn];namespace linetree
{#define lch(p) p*2#define rch(p) p*2+1struct treenode{int tag,mn;}tr[maxn*8];inline void build(int p,int l,int r){tr[p].mn=1e9;if(l==r) return ;int mid=(l+r)>>1;build(lch(p),l,mid),build(rch(p),mid+1,r);}inline void pushup(int p){tr[p].mn=min(tr[lch(p)].mn,tr[rch(p)].mn);}inline void pushdown(int p,int l,int r){if(tr[p].tag){int mid=(l+r)>>1;tr[lch(p)].tag=tr[p].tag;tr[rch(p)].tag=tr[p].tag;tr[lch(p)].mn=tr[p].tag-mid+1;tr[rch(p)].mn=tr[p].tag-r+1;tr[p].tag=0;}}inline void change(int p,int l,int r,int lx,int rx,int val)//区间赋值{if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){tr[p].tag=val;tr[p].mn=val-r+1;return ;}pushdown(p,l,r);int mid=(l+r)>>1;change(lch(p),l,mid,lx,rx,val),change(rch(p),mid+1,r,lx,rx,val);pushup(p);}inline int qry(int p,int l,int r,int lx,int rx){if(r<lx||l>rx) return 1e9;if(lx<=l&&r<=rx) return tr[p].mn;pushdown(p,l,r);int mid=(l+r)>>1;return min(qry(lch(p),l,mid,lx,rx),qry(rch(p),mid+1,r,lx,rx));}
}struct DSU
{int f[maxn];inline void init(int n){for(int i=1;i<=n;i++) f[i]=i;}inline int fr(int u){return f[u]==u?u:f[u]=fr(f[u]);}inline void merge(int u,int v){u=fr(u),v=fr(v);if(u!=v) f[u]=v;}
}F;int main()
{scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) pre[i]=lst[a[i]],lst[a[i]]=i;for(int i=1;i<=2e6;i++) lst[i]=n+1;for(int i=n;i;i--) nxt[i]=lst[a[i]],lst[a[i]]=i;F.init(n+1);linetree::build(1,1,n);scanf("%d",&q);for(int i=1;i<=q;i++) scanf("%d%d",&l[i],&r[i]),vec[r[i]].emplace_back(i);for(int i=1;i<=n;i++){linetree::change(1,1,n,pre[i]+1,i,i);F.merge(pre[i],pre[i]+1);for(auto v:vec[i]){int p=F.fr(l[v]);ans[v]=linetree::qry(1,1,n,l[v],p);}}for(int i=1;i<=q;i++) printf("%d\n",ans[i]);
}

线段树合并

P6773 NOI2020 命运

见题解 P6773 NOI2020 命运 - 彬彬冰激凌 - 博客园。

处理树上问题的利器，树的特殊分析使其仅带上的单 \(\log\) 复杂度极为优秀。

使用线段树来表示 dp 的某个维度也是常见手法。合并作为一次状态的转移，通过调度合适的遍历顺序、讨论出现节点缺失及叶子节点时的转移，以此优化复杂度。

推荐练习：P7563 JOISC 2021 Day4 最悪の記者 4 (Worst Reporter 4) - 彬彬冰激凌 - 博客园

线段树分裂

类似于 fhq-treap 的分裂，只不过每次裂开的地方需要新开一个节点来保持树的结构，当然直接归并到另外一棵树上的部分不用。

可持久化线段树

ICPC2023 杭州站 K. Card Game

考虑设 \(f_{l,r}\) 为游戏区间为 \([l,r]\) 时剩余的牌数，设 \(nxt_i\) 为下一张与 \(a_i\) 相同的牌的位置，有转移：

\[f_{l,r}=\begin{cases}0 &l>r\\ f_{l+1,r}+1 &l\leq r \wedge r<g_l\\ f_{g_l+1,r} &l\leq r \wedge r>g_l\end{cases} \]

考虑线段树维护第二维，由于需要强制在线，自然的想到需要可持久化。

对于从 \(f_{g_l+1,r}\) 的区间更新也需要连向线段树 \(g_l+1\) 这个版本，\(l+1\) 同理。

这里需要使用标记永久化的 trick 优化空间。

#include<bits/stdc++.h>
using namespace std;const int maxn=3e5+5;int n,q;
int a[maxn],lst[maxn],rt[maxn];namespace wzytree
{#define lch(p) tr[p].lch#define rch(p) tr[p].rchint tot=0;struct treenode{int lch,rch,tag;}tr[maxn*80];inline void add(int &p1,int p2,int l,int r,int lx,int rx,int val){if(r<lx||l>rx) return ;p1=++tot;tr[p1]=tr[p2];if(lx<=l&&r<=rx){tr[p1].tag+=val;return ;}int mid=(l+r)>>1;add(lch(p1),lch(p2),l,mid,lx,rx,val);add(rch(p1),rch(p2),mid+1,r,lx,rx,val);}inline void chg(int &p1,int p2,int l,int r,int pos,int val){p1=++tot;tr[p1]=tr[p2];val+=tr[p1].tag;if(l==r){tr[p1].tag-=val;return ;}int mid=(l+r)>>1;if(pos<=mid) chg(lch(p1),lch(p2),l,mid,pos,val);else chg(rch(p1),rch(p2),mid+1,r,pos,val);}inline void move(int &p1,int p2,int l,int r,int lx,int rx,int val1,int val2){if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){p1=++tot;tr[p1]=tr[p2];tr[p1].tag+=val2-val1;return ;}val1+=tr[p1].tag;val2+=tr[p2].tag;int mid=(l+r)>>1;move(lch(p1),lch(p2),l,mid,lx,rx,val1,val2);move(rch(p1),rch(p2),mid+1,r,lx,rx,val1,val2);}inline int qry(int p,int l,int r,int pos){if(l==r) return tr[p].tag;int mid=(l+r)>>1;if(pos<=mid) return tr[p].tag+qry(lch(p),l,mid,pos);else return tr[p].tag+qry(rch(p),mid+1,r,pos);}
}int main()
{scanf("%d%d",&n,&q);for(int i=1;i<=n;i++) scanf("%d",&a[i]),lst[i]=n+1;for(int i=n;i;i--){int g=lst[a[i]];wzytree::add(rt[i],rt[i+1],1,n,i,g-1,1);if(g<=n) wzytree::chg(rt[i],rt[i],1,n,g,0);if(g+1<=n) wzytree::move(rt[i],rt[g+1],1,n,g+1,n,0,0);lst[a[i]]=i;}int lstans=0;for(int i=1;i<=q;i++){int l,r;scanf("%d%d",&l,&r);l^=lstans,r^=lstans;printf("%d\n",lstans=wzytree::qry(rt[l],1,n,r));}
}

线段树维护 dp 的总结

树形 dp

树上 dp 且转移自带偏序关系，转移呈现的分段明显，优先考虑使用线段树合并实现一次儿子到父亲的转移。

讨论合并时的顺序以及存在一个点为空情况下方程的变形，借助题目要求和 dp 方程的特点设计懒标记和上传的信息。

通常将时空复杂度从 \(O(n^2)\) 优化至 \(O(n\log n)\)。

朴素 dp

同样对转移的分段有强关联，与树形 dp 不同的是，线段树合并在序列上无法保持良好的复杂度。使用可持久化的线段树维护继承，段落覆盖和区间相加。

特点在于继承的节点的数目不多，可以拆分成若干区间形式的操作。

历史信息

P6109 Ynoi2009 rprmq1

不一定好的阅读体验 P6109 Ynoi2009 rprmq1 - 彬彬冰激凌 - 博客园。

把矩阵关于 \(l_1,r_1\) 的那一个维度离线下来，另一维开线段树维护，每次暴力跑与查询区间 \([l_1',r_1']\) 有交集的修改，使用历史最值线段树维护。

更进一步，离线操作到 \(l\) 和 \(r+1\) 处，各做一次 \(+v\) 或 \(-v\)。查询 \([l_1',r_1']\) 放到猫树上，将指针移动到区间中点 \(mid\)，依次做 \(mid\) 到 \(l_1'\) 的各项操作，记录从 \(mid\) 开始出现的历史最值，最终在 \(l_1'\) 处查询区间 \([l_2',r_2']\) 的历史最值。\(r_1'\) 同理。

讨论线段树应该实现的功能：

• 区间修改。
• 区间历史最值查询。
• 将历史最值设为当前最值。

仿照当前最值的形式，设计历史最值应该维护的懒标记和上传值。

首先有 \(mx,add\) 为区间当前最值和当前加懒标记。

设计 \(hmx\) 为历史最值。

由于有区间修改操作，设计 \(hadd\) 为“上次下传后到当前时刻”出现的最大的加懒标记。

所以儿子的 \(mx\) 与自己的 \(hadd\) 相加为“上次下传后到当前时刻”出现的历史最大值。

因为当一个修改落到所表示自己的节点时，自身节点的值已经被修改更新（包括历史最值与懒标记），所以懒标记只可以用来为自己的儿子服务。

下传时，做以下几个步骤：

1. 用自己的 \(hadd\) 与儿子的 \(add\)，更新儿子的 \(hadd\)，即 \(son.hadd=\max(son.hadd,son.add+now.hadd)\)。
2. 用自己的 \(hadd\) 与儿子的 \(mx\) 更新儿子的 \(hmx\)，即 \(son.hmx=\max(son.hmx,son.mx+now.hadd)\)。
3. 更新儿子当前的 \(mx,add\)。

上传时，更新 \(hmx\) 与 \(mx\)。

上述步骤完成了历史最值的保存于查询。需要将历史最值设为当前值时，我们额外维护一个清空懒标记 \(clrtag\)，每次 \(clrtag\) 的覆盖区间都是 \([1,n]\)。

清空懒标记生效时，下传第一步把儿子的 \(hmx\) 与 \(hadd\) 设为无穷小。

此时的后续步骤，儿子的 \(hmx\) 与 \(hadd\) 会被自己的 \(hadd\) 更新为在可行时效内的历史最值。

#include<bits/stdc++.h>
using namespace std;#define ll long longconst int maxn=5e5+5;int n,m,id,cur,q,md;
int a[maxn],pos[maxn];ll ans[maxn];int cnt;
struct solder{int l,r,tim;}sr[maxn];
struct option{int l,r,v;};
struct qry{int id,l,r;};vector<option>chg[maxn];vector<qry>vec[20][maxn];namespace linetree
{#define lch(p) p*2#define rch(p) p*2+1struct treenode{ll add,hadd,mx,hmx;bool clrtag;}tr[maxn*8];inline void pushup(int p){tr[p].mx=max(tr[lch(p)].mx,tr[rch(p)].mx);tr[p].hmx=max(tr[lch(p)].hmx,tr[rch(p)].hmx);}inline void pushdown(int p){if(tr[p].clrtag){tr[lch(p)].clrtag=tr[rch(p)].clrtag=1;tr[lch(p)].hadd=tr[rch(p)].hadd=-1e18;tr[lch(p)].hmx=tr[rch(p)].hmx=-1e18;tr[p].clrtag=0;}tr[lch(p)].hadd=max({tr[lch(p)].hadd,tr[lch(p)].add+tr[p].hadd});tr[rch(p)].hadd=max({tr[rch(p)].hadd,tr[rch(p)].add+tr[p].hadd});tr[lch(p)].hmx=max(tr[lch(p)].hmx,tr[lch(p)].mx+tr[p].hadd);tr[rch(p)].hmx=max(tr[rch(p)].hmx,tr[rch(p)].mx+tr[p].hadd);tr[lch(p)].mx+=tr[p].add;tr[rch(p)].mx+=tr[p].add;tr[lch(p)].add+=tr[p].add;tr[rch(p)].add+=tr[p].add;tr[p].add=0,tr[p].hadd=0;}inline void change(int p,int l,int r,int lx,int rx,int val){if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){tr[p].add+=val;tr[p].hadd=max(tr[p].hadd,tr[p].add);tr[p].mx+=val;tr[p].hmx=max(tr[p].hmx,tr[p].mx);return ;}pushdown(p);int mid=(l+r)>>1;change(lch(p),l,mid,lx,rx,val);change(rch(p),mid+1,r,lx,rx,val);pushup(p);}inline ll qry(int p,int l,int r,int lx,int rx){if(r<lx||l>rx) return -1e18;if(lx<=l&&r<=rx) return tr[p].hmx;pushdown(p);int mid=(l+r)>>1;return max(qry(lch(p),l,mid,lx,rx),qry(rch(p),mid+1,r,lx,rx));}inline void clrtag(){pushdown(1);tr[1].clrtag=1;tr[1].hmx=tr[1].mx;}
}
namespace meowtree
{#define lch(p) p*2#define rch(p) p*2+1inline void build(int p,int l,int r,int dep){md=max(md,dep);if(l==r){pos[l]=p;return ;}int mid=(l+r)>>1;build(lch(p),l,mid,dep+1),build(rch(p),mid+1,r,dep+1);}inline void Go(int mid){while(cur<mid){cur++;for(auto v:chg[cur]) linetree::change(1,1,n,v.l,v.r,v.v);}while(cur>mid){for(auto v:chg[cur]) linetree::change(1,1,n,v.l,v.r,-v.v);cur--;}linetree::clrtag();}inline void solve(int p,int l,int r,int dep){int mid=(l+r)>>1;if(l==r){Go(mid);for(auto v:vec[dep][mid]) ans[v.id]=max(ans[v.id],linetree::qry(1,1,n,v.l,v.r));return ;}Go(mid);for(int i=mid;i>=l;i--){for(auto v:vec[dep][i]) ans[v.id]=max(ans[v.id],linetree::qry(1,1,n,v.l,v.r));for(auto v:chg[cur]) if(-v.v<0) linetree::change(1,1,n,v.l,v.r,-v.v);for(auto v:chg[cur]) if(-v.v>0) linetree::change(1,1,n,v.l,v.r,-v.v);cur--;}Go(mid);for(int i=mid+1;i<=r;i++){cur++;for(auto v:chg[cur]) if(v.v<0) linetree::change(1,1,n,v.l,v.r,v.v);for(auto v:chg[cur]) if(v.v>0) linetree::change(1,1,n,v.l,v.r,v.v);for(auto v:vec[dep][i]) ans[v.id]=max(ans[v.id],linetree::qry(1,1,n,v.l,v.r));}solve(p*2,l,mid,dep+1),solve(p*2+1,mid+1,r,dep+1);}
}int main()
{memset(ans,-0x7f,sizeof(ans));scanf("%d%d%d",&n,&m,&q);int len=1;while(len<n) len*=2;meowtree::build(1,1,len,1);for(int i=1;i<=m;i++){int lx,rx,ly,ry,x;scanf("%d%d%d%d%d",&lx,&ly,&rx,&ry,&x);chg[lx].push_back({ly,ry,x});chg[rx+1].push_back({ly,ry,-x});}for(int i=1;i<=q;i++){int lx,rx,ly,ry;scanf("%d%d%d%d",&lx,&ly,&rx,&ry);if(lx==rx){vec[md][lx].push_back({i,ly,ry});continue;}int dep=(int)log2(pos[lx])-(int)log2(pos[lx]^pos[rx]);vec[dep][lx].push_back({i,ly,ry});vec[dep][rx].push_back({i,ly,ry});}meowtree::solve(1,1,len,1);for(int i=1;i<=q;i++) printf("%lld\n",ans[i]);
}

势能线段树

loj 6029. 「雅礼集训 2017 Day1」市场

如果没有单点相加的操作，对不为 \(0\) 的区间暴力向下转移除法，复杂度是 \(O(n\log V)\) 的，每个点势能由 \(a_i\) 变到 \(0\) 至多 \(\log V\) 次。

加上单点相加后，我们考虑这样以下两种情况：

1. 区间内所有数相等，相当于一次区间赋值。

2. 但区间如果是 \(2^k\) 与 \(2^k-1\) 两种数交替出现，多次执行 \(d=2\)，每一次都无法作为区间赋值快速返回。

   但你会发现，除完后数之间的差没有发生变化，是不是可以看作一次区间相减呢？

   进一步讨论，设区间最大值 \(a=pd+r\)，最小值 \(q=qd+s\)。

   \[p-q=pd+r-qd-s\\ p-q=(p-q)d+r-s\\ (d-1)(p-q)=s-r \]

   等号成立当且仅当，\(p=q\and s=r\) 或 \(p=q+1\and s=d-1\and r=0\)，在这种情况下相当于区间加。

我们现在讨论一下原题中加法操作带来的复杂度增加（由于笔者菜，以下复杂度相关内容不保真，欢迎各位评论区指出错误）。

每次相加影响的区间数目 \(\log n\)，需要对于每个区间需要额外花 \(\log V\) 次操作清空新增的势能。

复杂度为 \(O(m\log n\log V)\)。

#include<bits/stdc++.h>
using namespace std;#define inf 1e18
#define ll long long
#define int long longconst int maxn=1e5+5;int n,q;
int a[maxn];inline int work(int p,int d)
{if(p>0) return p/d;else{int det=(-p)%d;if(det) det=1;return p/d-det;}
}namespace linetree
{#define lch(p) p*2#define rch(p) p*2+1struct treenode{int mx,mn,chg,add,num;long long sum;}tr[maxn*12];inline void pushup(int p){tr[p].sum=tr[lch(p)].sum+tr[rch(p)].sum;tr[p].mx=max(tr[lch(p)].mx,tr[rch(p)].mx);tr[p].mn=min(tr[lch(p)].mn,tr[rch(p)].mn);}inline void pushdown(int p){if(tr[p].chg!=-inf){tr[lch(p)].add=tr[rch(p)].add=0;tr[lch(p)].mx=tr[rch(p)].mx=tr[lch(p)].mn=tr[rch(p)].mn=tr[p].chg;tr[lch(p)].chg=tr[rch(p)].chg=tr[p].chg;tr[lch(p)].sum=tr[lch(p)].num*tr[p].chg;tr[rch(p)].sum=tr[rch(p)].num*tr[p].chg;tr[p].chg=-inf;}tr[lch(p)].mx+=tr[p].add;tr[lch(p)].mn+=tr[p].add;tr[lch(p)].add+=tr[p].add;tr[lch(p)].sum+=tr[p].add*tr[lch(p)].num;tr[rch(p)].mx+=tr[p].add;tr[rch(p)].mn+=tr[p].add;tr[rch(p)].add+=tr[p].add;tr[rch(p)].sum+=tr[p].add*tr[rch(p)].num;tr[p].add=0;}inline void build(int p,int l,int r){tr[p].chg=-inf;tr[p].num=r-l+1;if(l==r){tr[p].mx=tr[p].mn=tr[p].sum=a[l];return ;}int mid=(l+r)>>1;build(lch(p),l,mid),build(rch(p),mid+1,r);pushup(p);}inline void add(int p,int l,int r,int lx,int rx,int val){if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){tr[p].add+=val;tr[p].sum+=tr[p].num*val;tr[p].mx+=val,tr[p].mn+=val;return ;}pushdown(p);int mid=(l+r)>>1;add(lch(p),l,mid,lx,rx,val);add(rch(p),mid+1,r,lx,rx,val);pushup(p);}inline void change(int p,int l,int r,int lx,int rx,int val){if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){if(work(tr[p].mx,val)==work(tr[p].mn,val)){tr[p].add=0;tr[p].chg=work(tr[p].mn,val);tr[p].mx=tr[p].mn=tr[p].chg;tr[p].sum=tr[p].num*tr[p].mn;return ;}else if(tr[p].mx-tr[p].mn==1){int det=tr[p].mx-(int)floor(1.0*tr[p].mx/(1.0*val));tr[p].add-=det;tr[p].mx-=det,tr[p].mn-=det;tr[p].sum-=tr[p].num*det;return ;}}pushdown(p);int mid=(l+r)>>1;change(lch(p),l,mid,lx,rx,val),change(rch(p),mid+1,r,lx,rx,val);pushup(p);}inline int qrymi(int p,int l,int r,int lx,int rx){if(r<lx||l>rx) return inf;if(lx<=l&&r<=rx) return tr[p].mn;pushdown(p);int mid=(l+r)>>1;return min(qrymi(lch(p),l,mid,lx,rx),qrymi(rch(p),mid+1,r,lx,rx));}inline long long qrysum(int p,int l,int r,int lx,int rx){if(r<lx||l>rx) return 0;if(lx<=l&&r<=rx) return tr[p].sum;pushdown(p);int mid=(l+r)>>1;return qrysum(lch(p),l,mid,lx,rx)+qrysum(rch(p),mid+1,r,lx,rx);}
}signed main()
{scanf("%lld%lld",&n,&q);for(int i=1;i<=n;i++) scanf("%lld",&a[i]);linetree::build(1,1,n);for(int i=1;i<=q;i++){int op,l,r,x;scanf("%lld%lld%lld",&op,&l,&r);l++,r++;if(op==1) {scanf("%lld",&x);linetree::add(1,1,n,l,r,x);}else if(op==2) {scanf("%lld",&x);linetree::change(1,1,n,l,r,x);}else if(op==3) printf("%lld\n",linetree::qrymi(1,1,n,l,r));else printf("%lld\n",linetree::qrysum(1,1,n,l,r));}
}

P10639 BZOJ4695 最佳女选手

复杂度太菜了不会证，根据吉老师的论文，复杂度在 \(O(m\log^2 n)\) 级。

均摊复杂度的分析

先咕着。

线段树二分

P4602 CTSC2018 混合果汁 - 洛谷

考虑一个小朋友怎么做？二分果汁的最低美味度，将美味度大于等于 \(mid\) 的果汁按单价升序排序，依次选取，检测在要求的金钱范围是否可以达到要求的体积。

由于现在有多个小朋友，把二分变为整体二分，把大于 \(mid\) 的果汁用单价做下标放到线段树上，维护区间的果汁的价格（单价乘以数量）的和。

把依次选取检测的过程放到线段树上，类似于做二分查找，找出金钱为 \(val\) 的情况下，可获得最大体积的果汁。

每次检测左子树的和是否大于当前的 \(val\)，如果是向左子树递归；否则答案加上左子树的体积，\(val\) 减去左子树的花费，向右子树递归。到达叶子时，返回当前的 \(val\) 还可以单独买多少体积的叶子节点种类的果汁。

#include<bits/stdc++.h>
using namespace std;#define ll long longconst int maxn=2e5+5;int n,m;
int cst[maxn];struct JUICE{int d,p,l,id;}p[maxn];
struct QRY{ll g,L;}qry[maxn];int q[maxn],q1[maxn],q2[maxn],ans[maxn];inline bool cmp1(JUICE a,JUICE b){return a.d<b.d;}
inline bool cmp2(JUICE a,JUICE b){return a.p<b.p;}namespace linetree
{#define lch(p) p*2#define rch(p) p*2+1struct treenode{ll val,lim;}tr[maxn*8];inline void pushup(int p){tr[p].val=tr[lch(p)].val+tr[rch(p)].val;tr[p].lim=tr[lch(p)].lim+tr[rch(p)].lim;}inline void insert(int p,int l,int r,int pos,ll val){if(l==r){tr[p].lim=val,tr[p].val=tr[p].lim*cst[l];return ;}int mid=(l+r)>>1;if(pos<=mid) insert(lch(p),l,mid,pos,val);else insert(rch(p),mid+1,r,pos,val);pushup(p);}inline ll qry(int p,int l,int r,ll val){int mid=(l+r)>>1;if(l==r){int res=min(val/cst[l],tr[p].lim);return res;}if(tr[lch(p)].val<val) return tr[lch(p)].lim+qry(rch(p),mid+1,r,val-tr[lch(p)].val);return qry(lch(p),l,mid,val);}
}int cur;inline void solve(int l,int r,int L,int R)
{if(L==R){if(L==1){while(cur>L) cur--,linetree::insert(1,1,n,p[cur].id,p[cur].l);for(int i=l;i<=r;i++){ll res=linetree::qry(1,1,n,qry[q[i]].g);if(res>=qry[q[i]].L) ans[q[i]]=p[L].d;}}else for(int i=l;i<=r;i++) ans[q[i]]=p[L].d;return ;}if(L>R) return ;int mid=(L+R)>>1,cnt1=0,cnt2=0;mid++;while(cur<mid) linetree::insert(1,1,n,p[cur].id,0),cur++;while(cur>mid) cur--,linetree::insert(1,1,n,p[cur].id,p[cur].l);for(int i=l;i<=r;i++){ll res=linetree::qry(1,1,n,qry[q[i]].g);if(res>=qry[q[i]].L) q2[++cnt2]=q[i];else q1[++cnt1]=q[i];}for(int i=1;i<=cnt1;i++) q[l+i-1]=q1[i];for(int i=1;i<=cnt2;i++) q[l+i+cnt1-1]=q2[i];solve(l,l+cnt1-1,L,mid-1),solve(l+cnt1,r,mid,R);
}int main()
{scanf("%d%d",&n,&m);cur=n+1;for(int i=1;i<=n;i++) scanf("%d%d%d",&p[i].d,&p[i].p,&p[i].l);sort(p+1,p+n+1,cmp2);for(int i=1;i<=n;i++) p[i].id=i,cst[i]=p[i].p;sort(p+1,p+n+1,cmp1);for(int i=1;i<=m;i++){q[i]=i;scanf("%lld%lld",&qry[i].g,&qry[i].L);}solve(1,m,1,n);for(int i=1;i<=m;i++) printf("%d\n",ans[i]==0?-1:ans[i]);
}

无平凡交区间的维护

黑白树 - 数据结构选讲2-李雷思问 - Becoder

题面

一棵 \(n\) 个点的有根树，每个点有两种颜色，每个点有黑白两种颜色。

维护 \(m\) 个操作，属于以下五种之一：

1. 改变一个点的颜色。
2. 使 \(x\) 在同一个同色连通块内的点加 \(val\)。
3. 查询 \(x\) 同色连通块的点权最大值。
4. 使链 \(x,y\) 上所有节点点权加上 \(val\)。
5. 给 \(x\) 所在子树内所有点点权加上 \(val\)。

\(n,m\leq 2\times 10^5,0\leq val \leq 10^5\)。

思路

有链相关操作，树链剖分是跑不掉的。把树拍成 dfn 序以后，可以把对一个连通块的操作看成大一个子树减去若干颜色不同的小子树。

我们考虑开黑白两棵线段树，接下来以黑树为例介绍算法流程。

如果一个点 \(u\) 是白色的，那我们就在 \(u\) 子树所表示的区间落到线段树上的 \(\log n\) 个节点都打上我们的特殊标记。

拥有特殊标记的节点不向父亲上传自身的贡献（不上传），同时父亲也不向其下传连通块有关的懒标记（不接受）。

同时我们发现两个性质：

1. 在同一个连通块内的点被标记覆盖的次数（线段树叶子到根路径上，每个节点被标记次数相加）相同，这个结论是必要不充分的。
2. 不属于同一个连通块的点一定被特殊标记覆盖。

由于 dfn 序特殊的包含性质，对于黑色点 \(u\) 来说，所有祖先的子树表示的区间一定包含 \(u\) 这个节点，剩下的节点所表示子树的区间都与 \(u\) 无关。那么 \(u\) 被标记覆盖的次数应该与连通块内其他点相同。

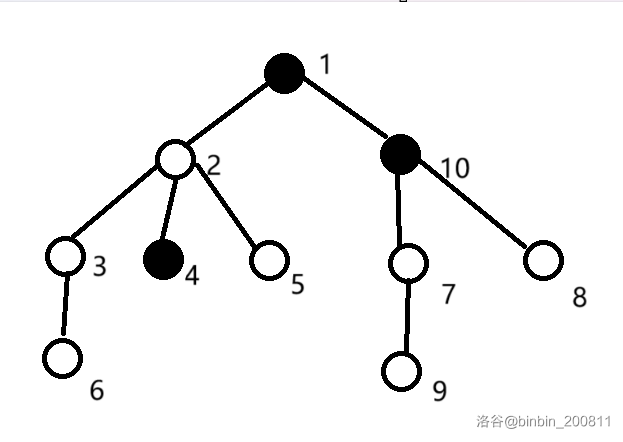
对于 \(2\) 被 \(1\) 覆盖了一次，同一连通块的 \(3\) 也被 \(1\) 覆盖一次。

对于 \(9\) 和 \(7\) 都被覆盖了 \(2\) 次，虽然 \(8\) 也被覆盖了两次，但 \(8\) 与 \(9,7\) 并不在同一个块内，因此性质 1 是必要而不充分的。

对于性质 2，不属于同一个连通块的点必然被至少一个祖先用特殊标记覆盖。

如何解决 \(1\) 操作的必要而不充分的问题呢？显然，加上了所属子树的限制后，覆盖次数相同的节点就是同色连通块内的节点了。

对于一个连通块 \(x\) 相关的查询或操作，需要找到与 \(x\) 在同色的连通块内最浅的祖先。

注意，同色连通块中的点在线段树上的覆盖次数，都由连通块中最浅的祖先的子树所对应的区间及更浅的区间提供。

找同色祖先的过程可以跳重链，用二分查找重链上某个点开始与 \(x\) 相同颜色的连续祖先，如果是重链顶就向上跳，否则当前点就是答案。同色判断可以用 dfn 序加树状数组或线段树，判断一段内是否相同颜色的数目刚等于段长度。注意一下，这里可以先判重链顶到当前节点全部同色，如果这样直接跳重链顶就行，由于只有一个链需要二分，复杂度为 \(O(\log^2 n)\)。

对于查询和操作首先，需要判断当前的区间是否与最浅祖先所在区间的覆盖次数相同，在此基础上对区间上做查询或更改。

剩下的部分与正常的线段树操作无异。

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define inf 1e18const int maxn=2e5+5;int n,m,cok;
int sz[maxn],hso[maxn],fa[maxn],dfn[maxn],fdfn[maxn],tp[maxn],dep[maxn],col[maxn],a[maxn];struct Edge
{int tot;int head[maxn];struct edgenode{int to,nxt;}edge[maxn*2];inline void add(int x,int y){tot++;edge[tot].to=y;edge[tot].nxt=head[x];head[x]=tot;}
}T;struct treearray
{int ts[maxn];inline int lowbit(int x){return x&(-x);}inline void add(int x,int y){for(;x<=n;x+=lowbit(x)) ts[x]+=y;}inline int qry(int x){int sum=0;for(;x;x-=lowbit(x)) sum+=ts[x];return sum;}inline int query(int l,int r){return qry(r)-qry(l-1);}
}Ts;struct linetree
{#define lch(p) p*2#define rch(p) p*2+1int flg=0;struct treenode{ll mx,coladd,add;int col;}tr[maxn*8];inline void pushup(int p){tr[p].mx=-1e18;if(!tr[lch(p)].col) tr[p].mx=max(tr[p].mx,tr[lch(p)].mx);if(!tr[rch(p)].col) tr[p].mx=max(tr[p].mx,tr[rch(p)].mx);}inline void pushdown(int p){tr[lch(p)].add+=tr[p].add;tr[lch(p)].mx+=tr[p].add;tr[rch(p)].add+=tr[p].add;tr[rch(p)].mx+=tr[p].add;tr[p].add=0;if(!tr[lch(p)].col){tr[lch(p)].coladd+=tr[p].coladd;tr[lch(p)].mx+=tr[p].coladd;}if(!tr[rch(p)].col){tr[rch(p)].coladd+=tr[p].coladd;tr[rch(p)].mx+=tr[p].coladd;}tr[p].coladd=0;}inline void build(int p,int l,int r,int flg){if(l==r){tr[p].mx=col[fdfn[l]]==flg?a[fdfn[l]]:-inf;return ;}int mid=(l+r)>>1;build(lch(p),l,mid,flg);build(rch(p),mid+1,r,flg);pushup(p);}inline void change(int p,int l,int r,int lx,int rx,int val){if(r<lx||l>rx) return ;if(lx<=l&&r<=rx){tr[p].col+=val;if(l!=r) {pushdown(p);pushup(p);}return ;}pushdown(p);int mid=(l+r)>>1;change(lch(p),l,mid,lx,rx,val);change(rch(p),mid+1,r,lx,rx,val);pushup(p);}inline void add(int p,int l,int r,int lx,int rx,int val,bool typ,int sum){if(r<lx||l>rx) return ;sum+=tr[p].col;if(lx<=l&&r<=rx){if(lx==l) flg=sum;if(typ) {if(sum==flg) tr[p].coladd+=val,tr[p].mx+=val;}else tr[p].add+=val,tr[p].mx+=val;return ;}pushdown(p);int mid=(l+r)>>1;add(lch(p),l,mid,lx,rx,val,typ,sum);add(rch(p),mid+1,r,lx,rx,val,typ,sum);pushup(p);}inline ll qry(int p,int l,int r,int lx,int rx,int col,int val){if(r<lx||l>rx) return -1e18;val+=tr[p].col;if(lx<=l&&r<=rx){if(lx==l) flg=val;if(val==flg) return tr[p].mx;return -1e18;}pushdown(p);int mid=(l+r)>>1;ll res1=qry(lch(p),l,mid,lx,rx,col,val),res2=qry(rch(p),mid+1,r,lx,rx,col,val);return max(res1,res2);}inline ll qrypos(int p,int l,int r,int pos){if(l==r){ll res=tr[p].mx;tr[p].mx=-inf;return res;}pushdown(p);int mid=(l+r)>>1;ll res=0;if(pos<=mid) res=qrypos(lch(p),l,mid,pos);else res=qrypos(rch(p),mid+1,r,pos);pushup(p);return res;}inline void chgpos(int p,int l,int r,int pos,ll val){if(l==r){tr[p].mx=val;return ;}pushdown(p);int mid=(l+r)>>1;if(pos<=mid) chgpos(lch(p),l,mid,pos,val);else chgpos(rch(p),mid+1,r,pos,val);pushup(p);}
}C[2];vector<int>vec[maxn];
inline void dfs1(int u,int f)
{sz[u]=1;fa[u]=f;dep[u]=dep[f]+1;for(int i=T.head[u];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(v==f) continue;dfs1(v,u);sz[u]+=sz[v];if(sz[v]>sz[hso[u]]) hso[u]=v;}
}
inline void dfs2(int u,int ftp)
{dfn[u]=++cok;fdfn[cok]=u;tp[u]=ftp;vec[ftp].emplace_back(u);C[col[u]^1].change(1,1,n,dfn[u],dfn[u]+sz[u]-1,1);Ts.add(dfn[u],col[u]);if(hso[u]) dfs2(hso[u],ftp);for(int i=T.head[u];i;i=T.edge[i].nxt){int v=T.edge[i].to;if(v==fa[u]||v==hso[u]) continue;dfs2(v,v);}
}inline int fr(int x)
{int flg=col[x];while(x){if(Ts.query(dfn[tp[x]],dfn[x])==(dep[x]-dep[tp[x]]+1)*flg){if(col[fa[tp[x]]]==flg) x=fa[tp[x]];else return tp[x];}else{int l=0,r=dep[x]-dep[tp[x]],ans=r;while(l<=r){int mid=(l+r)>>1;if(Ts.query(dfn[vec[tp[x]][mid]],dfn[x])==(dep[x]-dep[vec[tp[x]][mid]]+1)*flg)ans=mid,r=mid-1;elsel=mid+1;}return vec[tp[x]][ans];}}return 1;
}
inline void add(int x,int y,int val)
{for(;tp[x]!=tp[y];){if(dep[tp[x]]<dep[tp[y]]) swap(x,y);C[0].add(1,1,n,dfn[tp[x]],dfn[x],val,0,0);C[1].add(1,1,n,dfn[tp[x]],dfn[x],val,0,0);x=fa[tp[x]];}if(dep[x]>dep[y]) swap(x,y);C[0].add(1,1,n,dfn[x],dfn[y],val,0,0);C[1].add(1,1,n,dfn[x],dfn[y],val,0,0);
}inline bool check(int x,int tmp)
{int t=x;while(x!=tmp){x=fa[x];if(col[t]!=col[x]) return 1;}return 0;
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);T.add(u,v),T.add(v,u);}for(int i=1;i<=n;i++) scanf("%d",&col[i]);for(int i=1;i<=n;i++) scanf("%d",&a[i]);dfs1(1,0);dfs2(1,1);C[0].build(1,1,n,0);C[1].build(1,1,n,1);for(int i=1;i<=m;i++){int op,x,y,val;scanf("%d%d",&op,&x);if(op==1){C[col[x]^1].chgpos(1,1,n,dfn[x],C[col[x]].qrypos(1,1,n,dfn[x]));C[col[x]^1].change(1,1,n,dfn[x],dfn[x]+sz[x]-1,-1);C[col[x]].change(1,1,n,dfn[x],dfn[x]+sz[x]-1,1);Ts.add(dfn[x],col[x]?-1:1);col[x]^=1;}else if(op==2){scanf("%d",&val);x=fr(x);C[col[x]].add(1,1,n,dfn[x],dfn[x]+sz[x]-1,val,1,0);}else if(op==3){x=fr(x);printf("%lld\n",C[col[x]].qry(1,1,n,dfn[x],dfn[x]+sz[x]-1,col[x],0));}else if(op==4){scanf("%d%d",&y,&val);add(x,y,val);}else{scanf("%d",&val);C[0].add(1,1,n,dfn[x],dfn[x]+sz[x]-1,val,0,0);C[1].add(1,1,n,dfn[x],dfn[x]+sz[x]-1,val,0,0);}}
}

这种形式的线段树有启发性，但并不多见于比赛或者训练，希望有出题人大大普及。

后记

线段树时数据结构的重要组成部分，再趋向于数据结构与实际应用结合的情景下，\(polylog\) 的数据结构有着得天独厚的优势，对线段树更深层次的理解使用成为了解决部分优化问题的核心。