- 概
- 符号说明
- Popularity bias
- \(\mathbf{q}_1\) 和 \(\mathbf{r}\) 具有高相似度
- 相似度随着维度降低而增加
- 相似度随着训练的变化
- ReSN: Regulartion with Spectral Norm
Lin S., Gao C., Chen J., Zhou S., Hu B., Feng Y., Chen C. and Wang C. How do recommendation models amplify popularity bias? An analysis from the spectral perspective. WSDM, 2025.
概
本文分析在不引入额外的约束下, 基于矩阵分解的模型倾向于匹配 item 的流行度.
符号说明
- \(\mathcal{U}\), user set, \(|\mathcal{U}| = n\);
- \(\mathcal{I}\), item set, \(|\mathcal{I}| = m\);
- \(Y \in \{0, 1\}^{n \times m}\), interaction matrix;
- \(r_i = \sum_{u \in \mathcal{U}} y_{ui}\), 表示 item 的交互频率, 总的构成流行度向量 (popularity vector) \(\mathbf{r}\).
Popularity bias
-
我们考虑基于矩阵分解的方法, 它提供:
\[\mathbf{u}_u, \mathbf{v}_i, \]用以计算 user \(u\) 和 item \(i\) 之间的相似度
\[\hat{y}_{ui} = \mu (\mathbf{u}_u^T \mathbf{v}_i), \]这里 \(\mu(\cdot)\) 表示激活函数.
-
令 \(\mathbf{U} \in \mathbb{R}^{n \times d}, \mathbf{V} \in \mathbb{R}^{m \times d}\) 表示 user, item 的向量矩阵, 可得
\[\hat{\mathbf{Y}} = \mu (\mathbf{U} \mathbf{V}^T). \] -
对预估的得分矩阵 \(\hat{\mathbf{Y}}\) 进行 SVD 分解:
\[\tag{1} \hat{\mathbf{Y}} = \mathbf{P\Sigma Q^T} = \sum_{1 \le k \le L} \sigma_k \mathbf{p}_k \mathbf{q}_k^T, \quad L= \min(n, m), \]且 \(\sigma_1 \ge \sigma_2 \ge \ldots \ge \sigma_L\).
\(\mathbf{q}_1\) 和 \(\mathbf{r}\) 具有高相似度

-
上图展示了 (1) 中的主(右)奇异向量 \(\mathbf{q}_1\) 和 popularity vector \(\mathbf{r}\) 的 cosine 相似度:
\[\frac{\mathbf{q}_1^T \mathbf{r}}{\|\mathbf{q}_1\| \cdot \|\mathbf{r}\|} \]非常接近 1. 因此, 我们可以认为, 传统模型所学到的得分矩阵 \(\hat{\mathbf{Y}}\) 其实受到了非常非常多的流行度的影响.
-
进一步地, 我们可以理论证明这一点:
-
Theoerm 1 (Popularity memorization effect): 给定一个 embedding-based 的模型且具备足够的表达能力, 当 \(\mathbf{r}\) 服从 power-law, 我们有:
\[\cos (\mathbf{q}_1, \mathbf{r}) \ge \frac{\sigma_1^2}{r_{\max} \sqrt{\zeta (2 \alpha)}} \sqrt{1 - \frac{r_{\max} (\zeta (\alpha) - 1)}{\sigma_1^2} }, \]其中 \(r_{\max} = \max_i r_i\), \(\zeta (\alpha)\) 表示 Riemann zeta function \(\zeta (\alpha) = \sum_{j=1}^{\infty} \frac{1}{j^{\alpha}}\).
proof:
-
注意, 这里假设模型有足够的表达能力, 即假设 \(\hat{\mathbf{Y}}\) 能够足够近似 \(\mathbf{Y}\), 于是后面的分析相当于都是基于 \(\mathbf{Y}\) 的 SVD 分解之上.
-
于是
\[\cos(\mathbf{q}_1, \mathbf{r}) =\frac{\mathbf{q}_1^T \mathbf{r}}{\|\mathbf{r}\|} =\frac{\mathbf{q}_1^T \mathbf{Y}^T \mathbf{e}}{\|\mathbf{r}\|} =\frac{\sigma_1 \mathbf{p}_1^T \mathbf{e}}{\|\mathbf{r}\|}. \] -
又
\[\| \mathbf{r} \| = \sqrt{\sum_{i=1}^m r_i^2} =\sqrt{\sum_{i=1}^m (r_{\max} \cdot i^{-\alpha})^2} =r_{\max} \sqrt{\sum_{i=1}^m i^{-2\alpha}} \le r_{\max} \sqrt{\zeta (2 \alpha)}. \] -
于是
\[\cos (\mathbf{q}_1, \mathbf{r}) \ge \frac{\sigma_1 \mathbf{e}^T \mathbf{p}_1 }{\mathbf{r}_{\max} \sqrt{\zeta (2 \alpha)} }. \] -
后续需要 bound \(\sigma_1\) 和 \(\mathbf{e}^T \mathbf{p}_1\), 需要更多的符号引入 (详情请回看原文).
相似度随着维度降低而增加
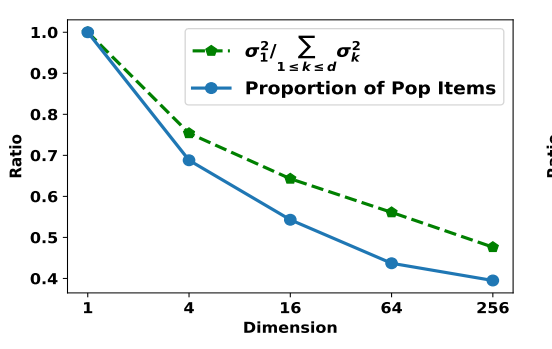
- 这个其实是比较显然, 因为维度降低总的能量降低了.
相似度随着训练的变化
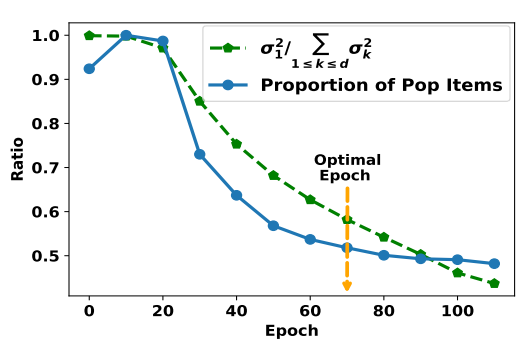
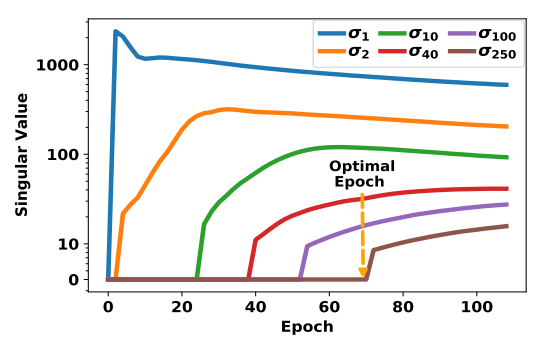
- 随着训练进行, popularity bias 的影响是逐步降低的, 但是过低实际上会导致效果的下降, 这似乎说明了 popularity bias 的需要维持在一定程度, 过低或这过高都不太好.
ReSN: Regulartion with Spectral Norm
-
本文提出的方法是:
\[\mathcal{L}_{\text{ReSN}} = \mathcal{L}_R (\mathbf{Y}, \hat{\mathbf{Y}}) + \beta \|\hat{\mathbf{Y}}\|_2^2, \]这里 \(\|\cdot \|^2\) 是谱范数.
-
但是这个计算是复杂的, 因此用如下的替代
\[\frac{\beta }{\| \mathbf{VU}^T \mathbf{e} \|^2 } \| \mathbf{UV^TVU}^T \mathbf{e} \|^2. \]相当于, 我们要求最后得到 score matrix 和流行度向量
\[\mathbf{V}\mathbf{U}^T \mathbf{e} \]的匹配度不能太高 (根据证明, \(\mathbf{V}\mathbf{U}^T \mathbf{e}\) 是比较接近 \(\mathbf{q}_1\) 的).