题目链接:https://www.acwing.com/problem/content/description/6134/
题意:
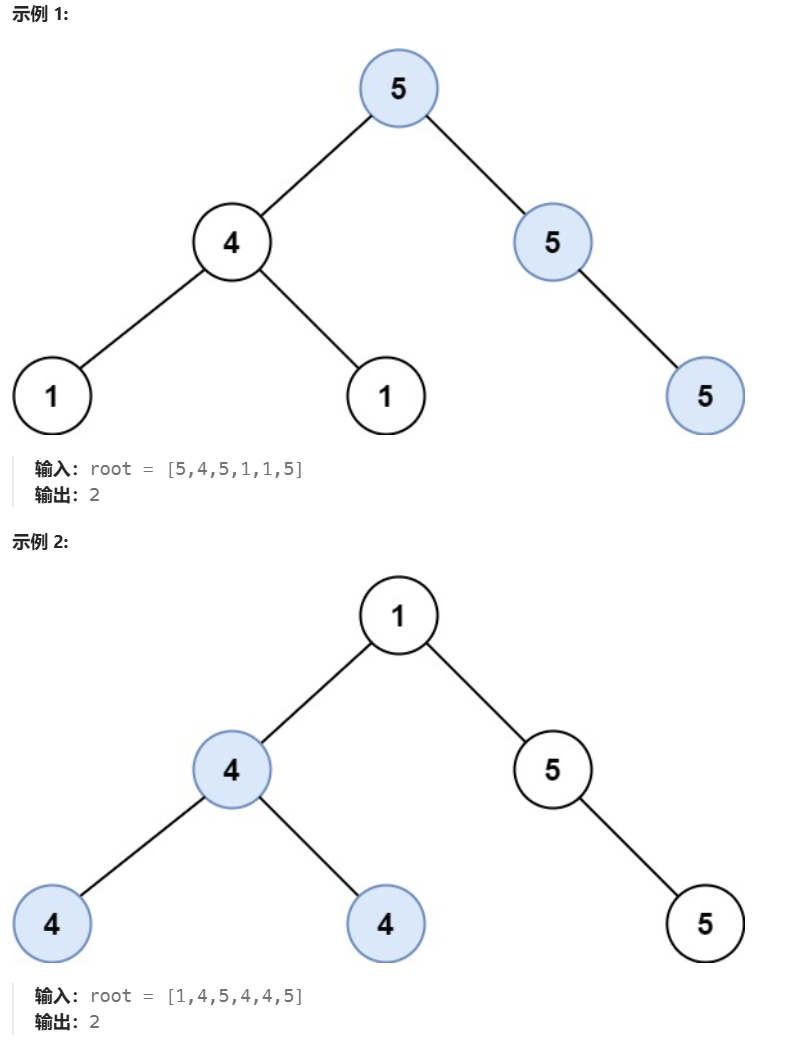
给定一个长度为n的数组a,一个模数m。每次可以对数组的一个元素+1或-1,让你求对某个x,对数组元素操作后,使(ai-x)%m==0 的最小操作数
思路:
使(ai-x)%m=0,即ai%m=x%m,不妨令x<m => ai%m=x
问题转化为:加减ai 使得ai mod m 等于相同的数字,由此可以想到中位数定理(即一个序列数字都转化为其中位数时,花费代价最小)
然而由于模数的运算 譬如 ai=8 ,m=9 ai%m=8 要想令其模数等于3 可以减5 也可以加4
发现 模数序列是在 一个环 上作运算的,(即环头为a1,环尾为an)(拆环成链:a[1] a[2] ···a[n] a[1] a[2] ···a[n] i~i+n-1 为一个环),那么在 环上 的每个数 都可以作为中位数 **
枚举i:1~n ,作为开头 那么p=i+n/2即中点**,分别求 左右两端 到 中点的距离,(这部分用前缀和实现)
注意的是 a[n+1] 到 a[n] 的距离 应该为 a[n+1]-a[n] +m,所以让拼接后片段都加上m
这样是正确的,因为环上的最短距离不会是绕远的
#include<bits/stdc++.h>
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define pb push_back
#define endl "\n"
#define int long long
#pragma GCC optimize(3)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int inf=0x3f3f3f3f;
const ll llmax=LLONG_MAX;
const int maxn=2e5+5;
const int mod=1e9+7;
int n,m;
int a[maxn];
int res[maxn];
int k[maxn*2];
int ans;
int pre[maxn*2];
signed main()
{ios::sync_with_stdio(false),cin.tie(0);int t;cin>>t;while(t--){ans=llmax;cin>>n>>m;rep(i,1,n) cin>>a[i];rep(i,1,n) {res[i]=a[i]%m;}sort(res+1,res+1+n);rep(i,1,n){k[i]=res[i];}rep(i,n+1,2*n){k[i]=res[i-n]+m;}rep(i,1,2*n){pre[i]=pre[i-1]+k[i];}rep(i,1,n){int p=i+n/2;int cnt=0;cnt+=(p-i)*k[p]-(pre[p-1]-pre[i-1]);cnt+=(pre[i+n-1]-pre[p])-(i+n-1-p)*k[p];ans=min(ans,cnt);}cout<<ans<<endl;} return 0;
}