原题
本来想当水题刷的,结果被水题刷了。。。70到80到90到100,必须写个题解记录一下(doge)
题目分析
一句话:求一个无权有向图中的最短环路(确保有环)
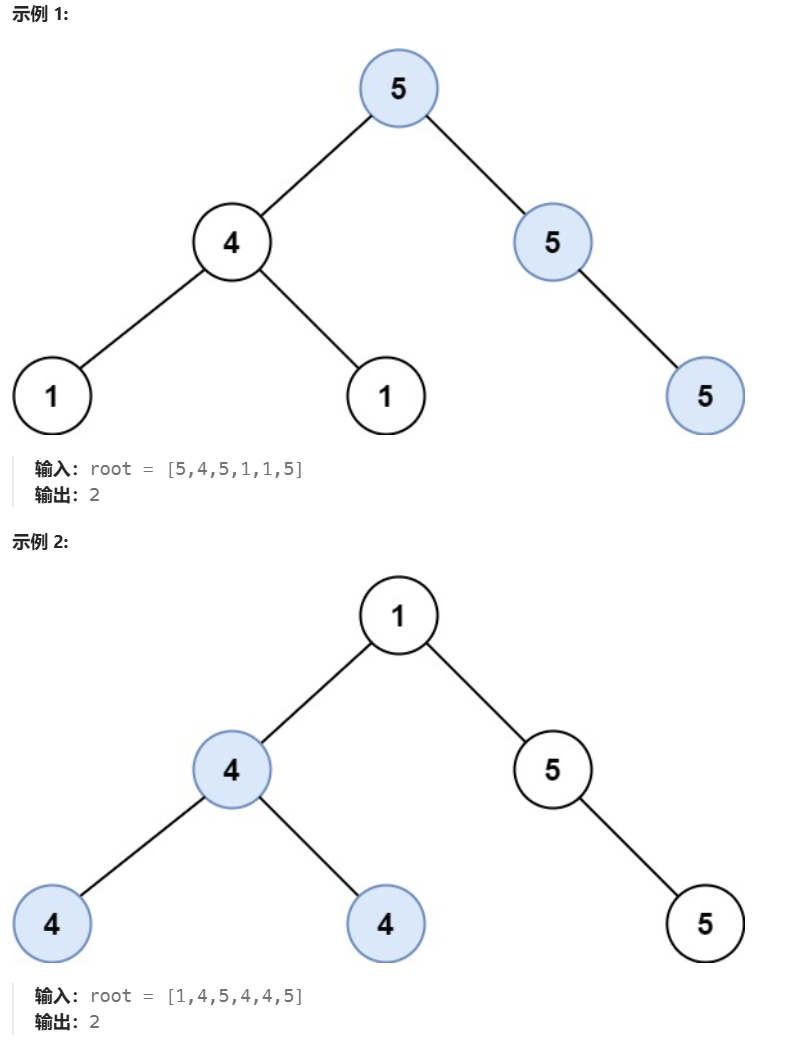
tip:每一个点出度为一,那么必然有环,以样例为例如下。

思路
没必要每轮模拟全部的传送,只看某一个人的传送过程:
就1而言:他的信息一次经过1-2-4-3-2...就无法回到1处,时间理解为∞。
就2而言:2-4-3-2,需要经过3轮,时间便为3。
就4,3而言:与2一样都在环里,也是3。
就5而言:不在环里是∞。
综上最快3轮结束游戏。
tip:这些题从不同点上看会比宏观看有奇效。
接下来我就想到了用染色法(万恶的开始),Son[i]记录i的传输对象,col[i]记录i的颜色(col=color),依次遍历每个点,在遍历第i个点时,把i染色成1,再找下一个也就是Son[i],然后Son[Son[i]]...如果发现某个p点的下一个点son[p]==1,说明已经被遍历过,侧面反映成为了环。

在找到环后对从当前的开始给环染第二遍色(p一定在环里,感性理解)每个环里的点都变成2,并且每染一次用一个变量记录,便是当前i收到自己的信息和游戏结束需要的时间。

但当时我嫌麻烦,就每读取一次i就初始化一次col[ ],结果爆掉了(难受)。所以尝试优先队列优化,果然多过了一个样例,然后艰难改到90分,最后终于修成正解!
1.减少染色次数:在原始代码中,每个节点被染色两次(1和2),优化后的代码中,每个节点只被染色一次,减少了不必要的操作。
2.最小环长度的记录:使用一个变量minn 来记录最小环的长度,避免了使用优先队列的开销。
3.循环优化:在检测环的过程中,使用 do-while 循环来确保环的长度计算正确,并且减少了不必要的条件判断。
代码过程
70分暴力染色代码如下
#include<bits/stdc++.h>
using namespace std;
const int N=20005;
int ans=10000008,cnt=0;
int fa[N],col[N];int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>fa[i];}for(int i=1;i<=n;i++){cnt=0;col[i]=1;int p=i;while(col[fa[p]]!=1){p=fa[p];col[p]++;}while(col[fa[p]]!=2){p=fa[p];col[p]=2;cnt++;}ans=min(ans,cnt);memset(col,0,sizeof col);}cout<<ans;return 0;
} 然后就...

呜呜呜...
80分暴力+优先队列优化代码
//在思考后,选用优先队列来代替min...
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int cnt=0,Son[N],col[N];
priority_queue<int,vector<int>,greater<int>> ans;int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>Son[i];}for(int i=1;i<=n;i++){if(col[i]) continue;cnt=0;col[i]=1;int p=i;while(col[Son[p]]!=1){p=Son[p];col[p]=1;}if(col[p]==1){while(col[Son[p]]!=2){p=Son[p];col[p]=2;cnt++;}ans.push(cnt);}p=i;while(col[p]<2){col[p]=2;p=Son[p];}}while(ans.top()==1){ans.pop();}cout<<ans.top();return 0;
} 
难受...
最后,优化了染色次数,终于AC!!!
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int Son[N],col[N];int main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++){cin>>Son[i];}int minn=N;for(int i=1;i<=n;i++){if(col[i]) continue;int cnt=0;int p=i;while(!col[p]){col[p]=1;p=Son[p];}if(col[p]==1){int start=p;do{cnt++;p=Son[p];}while(p!=start);minn=min(minn,cnt);}p=i;while(col[p]==1){col[p]=2;p=Son[p];}}if(minn==N){cout<<0;}else{cout<<minn;}return 0;
}
接下来也会更新拓扑做法,敬请期待!