ATR143B Counting Grids 学习笔记
Luogu Link
题意简述
现在需要将 \(1\sim n^2\) 共 \(n^2\) 个整数填进网格 \(S\)。定义一种方案合法当且仅当不存在 \(S_{i,j}\) 满足:
\[\max_{k=1}^n S_{i,k}=\min_{k=1}^n S_{k,j}=S_{i,j}
\]
。问合法方案数,答案对 \(998244353\) 取模。
\(n\le 500\)。
做法解析
看起来就正难则反,不合法方案大概率比合法方案少且好算。
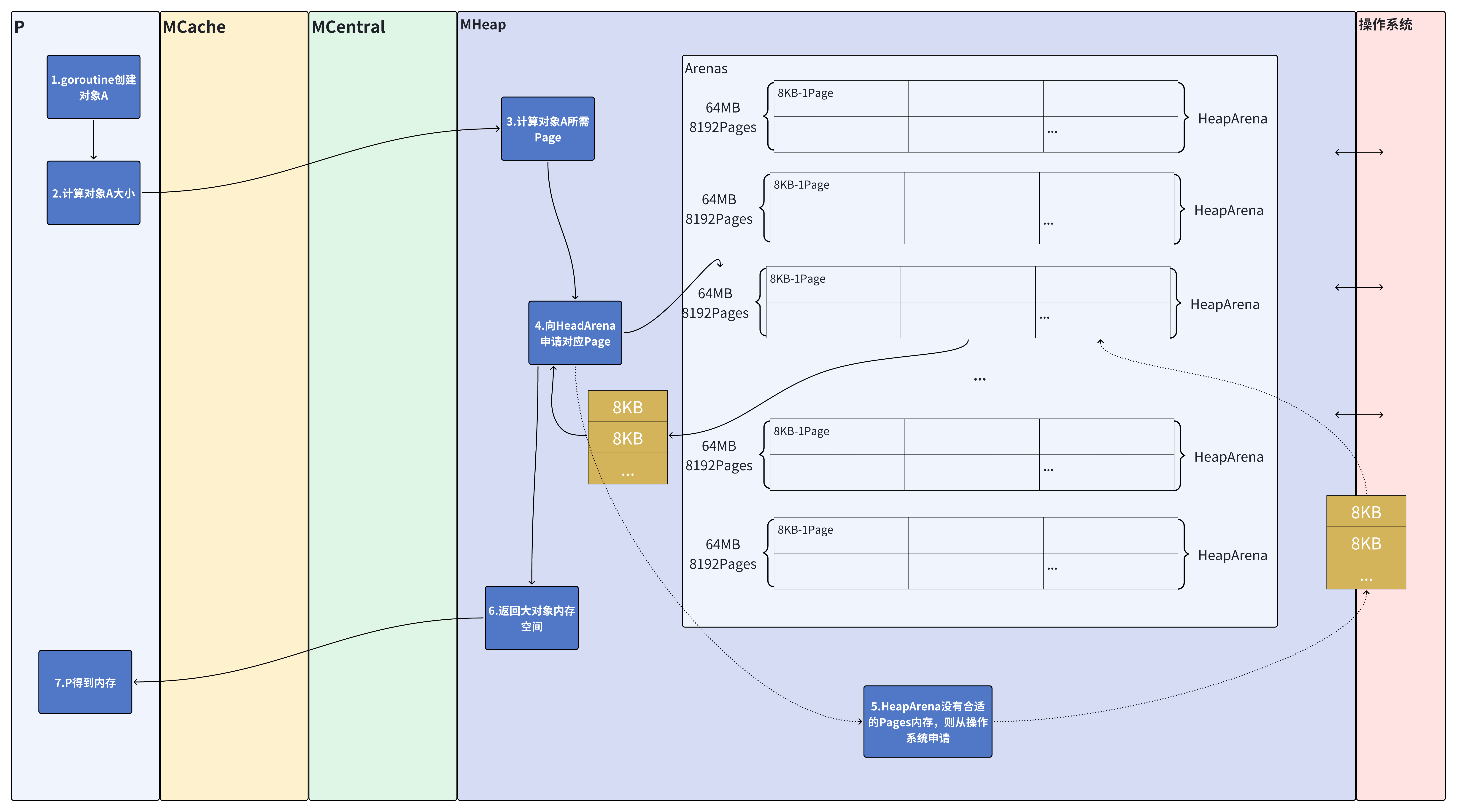
我们设不满足合法要求的元素为特殊元素,自然而然地我们要考虑其可能存在的数量,这关系到题目难度和是否使用容斥等工具。万幸地,这种特殊元素最多一个不然为什么洛谷只评了绿——如果有两个的话会相互矛盾(原因见图):

开始计算不合法方案数。首先特殊元素可以放在任何地方,是为 \(n^2\);如果特殊元素值为 \(i\) 的话,那么它所在列有 \(A_{i-1}^{n-1}\) 种填法,所在行有 \(A_{n^2-i}^{n-1}\) 种填法,其它元素随便填,方案为 \((n-1)^2!\)。总不合法方案数就是:
\[n^2(n-1)^2!\sum_{i=n}^{n^2-n+1}A_{i-1}^{n-1}A_{n^2-i}^{n-1}
\]
。合法方案数就是 \(n^2!\) 减去这玩意。
代码实现
最后一步别忘了取模!
#include <bits/stdc++.h>
using namespace std;
namespace obasic{typedef long long lolo;template <typename _T>void readi(_T &x){_T k=1;x=0;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')k=-1;for(;isdigit(ch);ch=getchar())x=(x<<3)+(x<<1)+ch-'0';x*=k;return;}template <typename _T>void writi(_T x){if(x<0)putchar('-'),x=-x;if(x>9)writi(x/10);putchar(x%10+'0');}
};
using namespace obasic;
const int MaxNs=2.5e5,Mod=998244353;
lolo facr[MaxNs],finv[MaxNs];
namespace omathe{lolo fastpow(lolo a,lolo b,lolo p){lolo res=1;for(;b;(a*=a)%=p,b>>=1)if(b&1)(res*=a)%=p;return res;}lolo getinv(lolo a,lolo p){return fastpow(a,p-2,p);}lolo Aran(lolo n,lolo m,lolo p){return facr[n]*finv[n-m]%Mod;}
};
using namespace omathe;
void prework(int n){facr[0]=finv[0]=1;for(int i=1;i<=n;i++)facr[i]=facr[i-1]*i%Mod;finv[n]=getinv(facr[n],Mod);for(int i=n-1;~i;i--)finv[i]=finv[i+1]*(i+1)%Mod;
}
int N;lolo ans;
int main(){readi(N);prework(N*N);for(int i=N;i<=N*N-N+1;i++)(ans+=Aran(i-1,N-1,Mod)*Aran(N*N-i,N-1,Mod)%Mod)%=Mod;(ans*=N*N*facr[(N-1)*(N-1)]%Mod)%=Mod;ans=(facr[N*N]+Mod-ans)%Mod;writi(ans);return 0;
}
反思总结
简单组合题,如果题目形如“不合法当且仅当有元素满足……”,而且这种元素数量大概不多,那就考虑它能有几个。
如果确认只有一个的话,难度可能就骤减了。