模型能否准确地预测数据,是通过损失函数来衡量的。如何调整权重和偏差参数,从而最小化神经网络的损失函数,这是一类特定的优化算法。我们称它们为优化器(optimizer)。
为什么需要优化器? 因为损失函数参数众多且结构复杂,其导数置零的方程无法得到解析解或计算非常复杂。因此我们需要用迭代的方式逐步调整参数, 确保每次优化都朝着最快降低损失的方向前进。
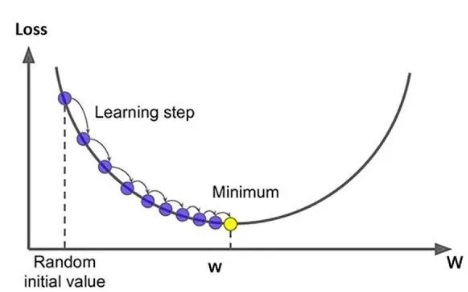
(图片来源:一文彻底搞懂深度学习 - 优化器(Optimizer)
本文讲解了一些常见的优化器,我们先回顾一下前面文章中提到的最基础的梯度下降法。
梯度下降法(Gradient Descent, GD)
梯度下降法的基本思想,是通过计算损失函数对参数的梯度来更新参数,沿着梯度的反方向逐步减小损失函数,最终达到最小化损失函数的目的,从而提高模型的准确性。

(Trask, Andrew W. Grokking Deep Learning. Shelter Island, New York: Manning, 2019.)
梯度下降法的变体:
- 批量梯度下降(BGD):每次更新使用全部训练样本,计算量大但收敛稳定。
- 随机梯度下降(SGD):每次更新随机选取一个样本,计算速度快但收敛过程可能波动较大。
- 小批量梯度下降(MBGD):每次更新使用一小批样本,是BGD和SGD的折中方案
下图中可以直观的感受到不同梯度下降法的收敛情况。
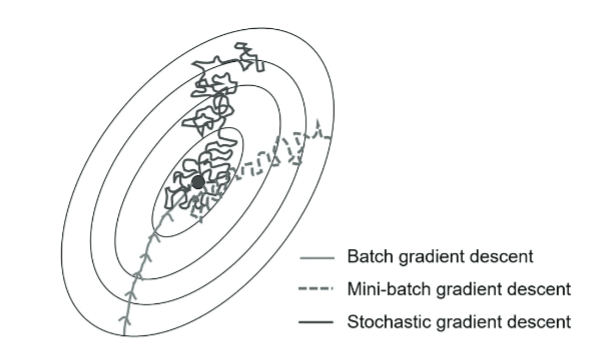
(Meedeniya, Dulani. Deep Learning: A Beginners’ Guide. 1st ed. New York: Chapman and Hall/CRC, 2023. )
动量法(Momentum)
动量法的基本思想,是在梯度下降的基础上加入动量项,通过累积历史梯度加速收敛并减少震荡。
我们看下面这张图,当我们初始化的w在图中蓝色部分时,此时运用梯度下降法有可能会导致我们进入局部最小值,而非全局最小值。
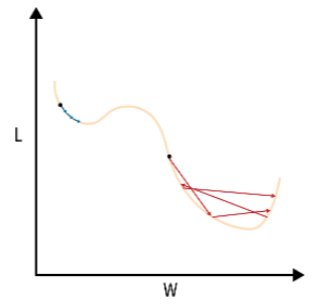
(Trask, Andrew W. Grokking Deep Learning. Shelter Island, New York: Manning, 2019.)
动量法的思想收到物理学中动量概念的启发。想象一个小球从图中蓝色部分处开始下落,当它到达局部最小点时,由于惯性的作用,并不会立即停下,而是会继续向右侧滚动,如果他的动量足够大,那么它就有可能滚出局部最小区域,继续往全局最小区域滚动。
此外,在梯度方向一致的区域(如损失函数的长斜坡),动量项的累积会逐步增大更新步幅,从而加速收敛;通过梯度加权平均,平滑了更新方向,在损失曲面陡峭或高曲率区域,这一机制能减少梯度方向的剧烈变化,避免“之字形”震荡(如图中红色收敛过程所示)。
从数学上,我们更新权重时,不仅利用当前的梯度,还利用了上一次迭代的梯度:
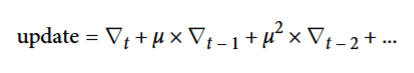
其中μ为衰减值,表示之前的梯度对本次更新的影响降低,越往前的梯度,影响呈指数级下降。
Nesterov加速梯度法(Nesterov Accelerated Gradient, NAG)
这种算法通过引入“前瞻”机制来加速收敛并减少震荡。在动量法的基础上,先根据动量项对参数进行预测更新,再计算梯度,从而更准确地估计下一步的位置。
NAG的更新公式如下:
-
临时参数更新:
\(θ_{temp}=θ_t−γv_t\)
其中,\(θ_t\)是第t次迭代的参数值,γ是动量系数,\(v_t\)是动量项。 -
计算梯度:
在临时参数\(θ_{temp}\)处计算梯度\(∇J(θ_{temp})\)。 -
更新动量项:
\(v_{t+1}=γv_t+η∇J(θ_{temp})\)
其中,η是学习率。 -
更新参数:
\(θ_{t+1}=θ_t−v_{t+1}\)
在普通动量法中,我们是结合历史动量和当前梯度进行参数的更新。而在NAG中,我们利用历史动量预测一个临时参数位置,用这个预测的临时参数位置的梯度,来“修正”我们的历史动量,从而更智能地调整参数更新方向。
Adagrad
当所需更新的参数(自变量)的梯度之间有较大差别时,我们需要选择足够小的学习率,避免在梯度值较大的维度上发散。但这样会导致在梯度值较小的维度上更新缓慢。AdaGrad算法,它可以根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,从而避免统一的学习率难以适应所有维度的问题。
更新过程分为两步:
- 梯度平方累积
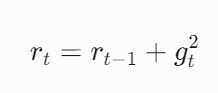
其中 \(r_t\) 表示时间步 t 的累积梯度平方,\(g_t\) 为当前梯度 - 参数更新
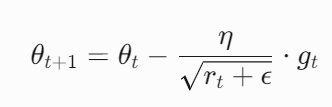
其中 η 是初始学习率,ϵ 为极小值(如 \(10^{−8}\))防止除零
从公式中可知,如果某一维度的梯度较大,则梯度平方的累积较大,学习率 η 下降的就比较快。反之,如果某一维度梯度较小,学习率下降较慢或增加。
从单一维度来说,由于梯度一直在累计历史的梯度平方,因此自变量每个元素一直是在降低的。所以如果学习率在早期降得较快,而当前解依然不佳时,AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解。
RMSprop
RMSprop(Root Mean Square Propagation)的基本思想,是对Adagrad的改进,使用梯度的指数加权平均来调整学习率,避免学习率过早衰减。具体步骤如下:
-
梯度平方的指数平均计算
对于每个参数,维护一个梯度平方的指数加权平均变量 st:
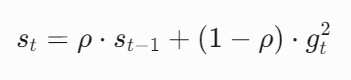
其中:
- ρ 为衰减率(通常设为0.9),控制历史梯度的影响权重;
- \(g_t\) 为当前时间步的梯度。
-
参数更新
调整后的学习率为原始学习率 η 除以梯度平方平均的平方根,并加入极小值 ϵ(如 \(10^{−8}\))防止分母为零:
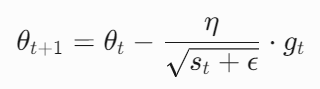
由公式可知,和AdaGrad算法一样,通过历史梯度的引入,调整不同梯度大小的参数的学习率:梯度较大的参数方向学习率减小,避免震荡;梯度较小的参数方向学习率增大,加速收敛。
与AdaGrad算法不同的是,这里引入了衰减率ρ,用来控制历史梯度的影响,使得算法对最近的梯度给予更多的权重,而对旧的梯度逐渐“遗忘”,从而减少了上文中学习率衰减过快的问题。
Adam
Adam(Adaptive Moment Estimation)了结合动量法和RMSprop的优点,通过一阶矩(均值)和二阶矩(方差)估计实现动态学习率调整:
-
动量计算

其中 β1(默认0.9)控制梯度均值衰减,β2(默认0.999)控制梯度方差衰减。
这里的mt就类似于动量法中的动量,是一种对历史动量的累计。
这里的vt就类似于RMSprop中的梯度平方累计,用于控制学习率。 -
偏差校正

由于m0初始化为0,会导致mt偏向于0,尤其在训练初期阶段。所以这里需要秀梯度均值进行偏差纠正,消除初始零值偏差,确保初期更新稳定性。
同理,也要对vt进行偏差纠正。 -
参数更新
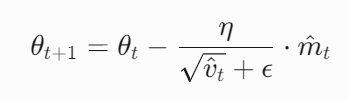
结合动量方向与自适应学习率,平衡收敛速度与稳定性。
总结
优化器的适用场景:
- GD及其变体:基础的梯度下降方法。
- Momentum、NAG:利用历史累计动量加速收敛,减少震荡。
- AdaGrad、RMSprop:自适应学习率,适合非平稳目标。
- Adam:综合性能优异,通常作为默认选择。
| 优化器 | 核心思想 | 适用场景 | 缺点 |
|---|---|---|---|
| GD | 全局最优方向 | 小数据集/凸问题 | 计算成本高 |
| SGD | 随机采样加速 | 在线学习 | 震荡严重 |
| Momentum | 惯性加速 | 高曲率区域 | 需调动量系数 |
| NAG | 前瞻性梯度计算 | 复杂损失曲面 | 实现复杂度稍高 |
| AdaGrad | 参数自适应学习率 | 稀疏数据 | 学习率过早衰减 |
| RMSprop/AdaDelta | 滑动窗口自适应 | 非平稳目标 | 对初始化敏感 |
| Adam | 动量+自适应 | 通用场景 | 可能错过更优解 |
(表格来自:常用优化器的原理及工作机制详解)