换根dp

概念

换根 \(dp\) ，又被称为二次扫描，是属于树形 \(dp\) 的一类但比一般树形dp更难。

特点

• 通常是没有指定根结点，且根结点的变化会对一些值产生影响。

• 通常需要两次 \(dfs\) ，第一次 \(dfs\) 预处理信息，第二次 \(dfs\) 开始换根动态规划。

• 求解的答案通常需要结合所有相连的结点，且一般都是多次询问某个点的答案。

优点

暴力求解的话，枚举每个结点作为根的情况再 \(dfs\) 扫描，这样就需要 \(O(n^2)\) 的时间复杂度，通常是不能够接受。而换根 \(dp\)，先进行一次扫描预处理信息后，再一次扫描进行动态规划解出所有节点的答案，时间复杂度优化为 \(O(n + n)\) ，这样就可以成功获取答案了。

解法一般形式

换根 \(dp\) 第一次扫描通常需要结合树形 \(dp\) 的思想，先任选一个结点 \(root\) 作为根结点，然后从根结点开始递归处理信息，但这时只有以 \(root\) 作为根结点的信息，所以需要在第二次扫描时，考虑换另一个结点为根时的答案，这时要通过第一次预处理出来的信息进行状态转移。

即：

• 以某个点（通常是 \(1\)）作为根节点进行第一次扫描，预处理信息。

• 依旧从这个点开始第二次扫描，但这次进行换根的动态规划，通常是结合父节点的信息合并统计答案。

题目讲解

数的中心

题目链接：AcWing 树的中心、洛谷 树的中心

题目大意：

给定一棵树，求这个树的中心。
树的中心：树上某个结点到最远的结点距离最近，那么这个结点就是树的中心。

思路：

首先建立以 \(1\) 为根的树，然后思考每个结点的最长距离会出现的路径：当前结点从某个子节点出发的最长路径，或从父节点出发的不再经过自己的最长路径。

所以，我们可以先第一次 \(dfs\) 扫描出每个结点从子结点出发的最长距离和次长距离，第二次扫描时结合父节点的数据更新当前结点为根时的最长距离。

处理次长距离的原因是：在进行换根的动态转移时，要结合父节点的最长路径，但如果父节点的最长路径恰好经过了当前结点，那么就要用父节点的次长路径来进行状态转移了。

AcWing代码

#include <iostream>
#include <cstring>using namespace std;const int INF = 0x3f3f3f3f;
const int N = 2e4 + 10;int n;
int h[N], e[N], w[N], ne[N], idx;
int d1[N], d2[N], up[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void dfs_d(int u, int fa)
{d1[u] = d2[u] = -INF;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;dfs_d(j, u);if (d1[j] + w[i] > d1[u]) d2[u] = d1[u], d1[u] = d1[j] + w[i];else if (d1[j] + w[i] > d2[u]) d2[u] = d1[j] + w[i];}if (d1[u] == -INF) d1[u] = d2[u] = 0;
}void dfs_u(int u, int fa)
{for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;up[j] = up[u] + w[i];if (d1[j] + w[i] != d1[u]) up[j] = max(up[j], d1[u] + w[i]);else up[j] = max(up[j], d2[u] + w[i]);dfs_u(j, u);}
}int main()
{memset(h, -1, sizeof h);cin >> n;for (int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}dfs_d(1, -1);dfs_u(1, -1);int res = INF;for (int i = 1; i <= n; i ++) res = min(res, max(d1[i], up[i]));cout << res;return 0;
}

洛谷代码

#include <iostream>
#include <cstring>using namespace std;const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;int n;
int h[N], e[N], ne[N], idx;
int d1[N], d2[N], up[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}void dfs_d(int u, int fa)
{d1[u] = d2[u] = -INF;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;dfs_d(j, u);if (d1[j] + 1 > d1[u]) d2[u] = d1[u], d1[u] = d1[j] + 1;else if (d1[j] + 1 > d2[u]) d2[u] = d1[j] + 1;}if (d1[u] == -INF) d1[u] = d2[u] = 0;
}void dfs_u(int u, int fa)
{for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;up[j] = up[u] + 1;if (d1[j] + 1 != d1[u]) up[j] = max(up[j], d1[u] + 1);else up[j] = max(up[j], d2[u] + 1);dfs_u(j, u);}
}int main()
{memset(h, -1, sizeof h);cin >> n;for (int i = 1; i < n; i ++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs_d(1, -1);dfs_u(1, -1);int res = INF;int ans1, ans2 = -1;for (int i = 1; i <= n; i ++) {int d = max(d1[i], up[i]);if (d < res) {res = d;ans1 = i;}else if (d == res) ans2 = i;}cout << ans1;if (~ans2 && max(d1[ans2], up[ans2]) == res) cout << ' ' << ans2;return 0;
}

---

[POI 2008] STA-Station

题目链接：洛谷 P3478

题目大意：

给定一个 \(n\) 个点的树，请求出一个结点，使得以这个结点为根时，所有结点的深度之和最大。

思路：

首先，我们依旧建立以 \(1\) 为根的树。定义 \(dp[i]\) 为：以 \(i\) 为根时深度之和。

接着，思考换根的状态转移，以样例距离

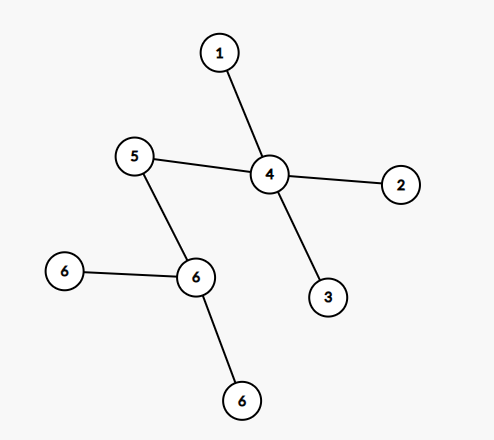
假设我们已经求出了以 \(1\) 为根的深度之和，那么当以 \(4\) 为根时，可以发现以 \(4\) 为根的子树的所有结点深度都减少了1，而不属于 \(4\) 为根的子树的结点的深度都增加了1，再举例以 \(5\) 为根时对比以 \(4\) 为根时也符合上面的推测，得出转移的公式：\(dp[v] = dp[u] - size[v] + n - size[v]\)

从上面的转移公式，可以知道我们第一次扫描需要预处理子树的结点个数和 \(dp[1]\) 的值。

点击查看代码

#include <iostream>
#include <vector>using namespace std;typedef long long ll;const int N = 1e6 + 10;int n;
vector<int> g[N];
ll c[N], dp[N], sum, ans;void dfs1(int u, int fa, int h)
{c[u] = 1;dp[1] += h;for (auto v : g[u]) {if (v == fa) continue;dfs1(v, u, h + 1);c[u] += c[v];}
}void dfs2(int u, int fa)
{for (auto v : g[u]) {if (v == fa) continue;dp[v] = dp[u] + n - 2 * c[v];dfs2(v, u);}if (dp[u] > sum) {sum = dp[u];ans = u;}
}int main()
{cin >> n;for (int i = 1; i < n; i ++) {int u, v;cin >> u >> v;g[u].emplace_back(v);g[v].emplace_back(u);}dfs1(1, -1, 0);dfs2(1, -1);cout << ans;return 0;
}

---