前言:阅读理解+剪枝+头脑风暴
Designed By FrankWkd 遵循GNU GPL2.0开源协议。
题目
P1731 [NOI1999] 生日蛋糕
题目背景
数据加强版 link
题目描述
7 月 17 日是 Mr.W 的生日,ACM-THU 为此要制作一个体积为 \(N\pi\) 的 \(M\) 层生日蛋糕,每层都是一个圆柱体。
设从下往上数第 \(i\)(\(1 \leq i \leq M\))层蛋糕是半径为 \(R_i\),高度为 \(H_i\) 的圆柱。当 \(i \lt M\) 时,要求 \(R_i \gt R_{i+1}\) 且 \(H_i \gt H_{i+1}\)。
由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 \(Q\) 最小。
请编程对给出的 \(N\) 和 \(M\),找出蛋糕的制作方案(适当的 \(R_i\) 和 \(H_i\) 的值),使 \(S=\dfrac{Q}{\pi}\) 最小。
(除 \(Q\) 外,以上所有数据皆为正整数)
输入格式
第一行为一个整数 \(N\)(\(N \leq 2 \times 10^4\)),表示待制作的蛋糕的体积为 \(N\pi\)。
第二行为 \(M\)(\(M \leq 15\)),表示蛋糕的层数为 \(M\)。
输出格式
输出一个整数 \(S\),若无解,输出 \(0\)。
输入输出样例 #1
输入 #1
100
2
输出 #1
68
思路
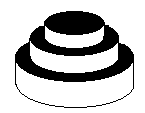
我们先来解决 \(S=\dfrac{Q}{\pi}\),那么众所周知,\(Q=\) 所有圆环(柱)的上表面面积 \(+\) 侧面面积 ,那么我们看下图:
 图源侵删
图源侵删
该图中的黑色部分就是我们要计算的圆环(柱)的上表面面积,我们将整合图形从上到下拍扁,就得到了一个圆柱,这个圆柱的上表面面积(也就是一个圆)就是图中黑色部分的面积。(我们设 \(R_i\) 和 \(H_i\) 为第 \(i\) 层的半径和体积)
那么第 \(1\sim i\) 层的表面积
所以说 \(S\) 就是去掉 \(\pi\) 后的图形表面积。也就是 \(\sum2R_{i}H_{i}+R_{M}^{2}\)
本题就转化成了求该图形的表面积除 \(\pi\) 后的值(是整数)。
剪枝
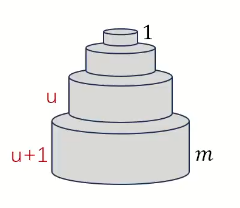
我们设最上层的编号为 \(1\),当前 \(DFS\) 的层数为 \(u\) ,总层数为 \(m\),如下图(\(u+1\) 不一定等于 \(m\)):
优化搜索顺序
- 我们从下向上搜索,因为下层面积大,分支少。
- 每一层的 \(R\) 和\(H\) 从大到小枚举,因为开始的时候枚举大的数据分支就会变小,搜到数据时累计的循环次数就会比先暴搜小分支的时候小。
上下界剪枝 (接下来所有公式和等式均忽略 \(\pi\))
现在我们要确定 \(R_u\) 和 \(H_u\) 的范围。
- 最小值:因为当前再第 \(u\) 层,第 \(1\) 层的最小值为 \(1\),第 \(2\) 层的最小值为 \(2\),以此类推,第 \(u\) 层的 \(R_u\) 和 \(H_u\) 的最小值为 \(u\)。
- 最大值:
- 我们当前已经确定了第 \(m\sim u+1\) 层的 \(R\) 和 \(H\),我们设第 \(m\sim u+1\) 层的体积和为 \(v\) ,那第 \(1\sim u\) 层的体积和为 \(n-v\) ,那当前这一层的体积肯定小于等于还未计算所有体积,即 \(R_u^2H_u\le n-v\)。既然我们要计算 \(R_u\) 的最大值,那么我们不妨将 \(H_u\) 设为 \(1\) ,即 \(R_u^2\le n-v\),\(R_u\le \sqrt{n-v}\).
- 根据题目内容,\(R_i >R_{i+1}\) ,因为我们是反向遍历的,所以就是 \(R_u < R_{u+1}\) 。\(H_u\) 同理.
可行性剪枝
我们预处理出 \(1\sim m\) 层的最小体积 \(minv[i]\) 表示第 \(1\sim i\) 层的最小体积,如果当前已经算出来的 \(u+1\sim m\) 层的体积 \(v\) 加上 \(minv[u]\) 大于总体积 \(n\) 的话,就直接 \(return\) 。
最优化剪枝
我们预处理出 \(1\sim m\) 层的最小表面积 \(mins[i]\) 表示第 \(1\sim i\) 层的最小表面积,如果当前已经算出来的 \(u+1\sim m\) 层的表面积 \(s\) 加上 \(mins[u]\) 大于当前已经搜到的合法答案的最小资 \(ans\) 的话,就直接 \(return\) 。
 图源侵删
图源侵删
最优化剪枝 Plus (遇事不明请看上图)
\(1\sim u\) 层的最小侧面积和还可以用剩余体积 \(n-v\) 来估价。
\(1\sim u\) 层的体积和为: \(\sum_{i=1}^{{u}}{R}_{{i}}^{2}*{H}_{{i}}=n-v\),
\(1\sim u\) 层的侧面积和 \(2\sum _{{i= 1}}^{{u} }R_{{i} }* H_{{i} }\)
提公因式 \(R_u\) 得:
因为我们是使用 \(\sum_{i=1}^{u}\) 遍历 \(1\sim u\) 中的所有数,所以肯定保证 \(i \le u\).这里我也理解了好长时间,\(\sum_{i=1}^{u}\) 等同于:for(int i = 1;i <= u;i++) ,所以在 \(for\) 里面执行的时候 \(i\) 一定 \(\le u\). 我们把原式中的的一个 \(R_u\) 换成 \(R_i\),这个式子肯定是小于等于没换的式子的。即:
还记得 \(1\sim u\) 层的体积和吗?\(\sum_{i=1}^{{u}}{R}_{{i}}^{2}*{H}_{{i}}=n-v\)
将 \(\frac 2{{R_{u}} }\sum _{{i= 1}}^{{u} }R_{{i} }^{2}* H_{{i} }\) 中的 \(\sum_{i=1}^{{u}}{R}_{{i}}^{2}*{H}_{{i}}\) 替换为 \(n-v\) ,就变成了 \(\frac{2(n-v)}{R_{u}}\)。
这时你会发现 \(R_u\) 是未知的! 我们将 \(R_u\) 替换为 \(R_{u+1}\) 这时候,\(\frac{2(n-v)}{R_{u+1}}<\frac{2(n-v)}{R_{u}}\)
所以,如果 \(s+\frac{2({n}-{v})}{{R}_{u+1}}>ans\),既然小的那个式子 \(+s\) 都比当前的最优解差,那么 \(s+\frac{2(n-v)}{R_{u}}\) 一定大于当前的最优解 \(ans\),那么剪枝。
该估价不等式类似 \(A^*\)算法中的估价函数思想。(\(\frac{2(n-v)}{R_{u+1}}+s\) 类似于估价函数)
数据梳理
-
体积: \(n=\sum_{i=1}^mR_i^2H_i\)
-
面积:\(S=\sum2R_iH_i+R_M^2\)
-
剪枝:
- 1.优化搜索顺序
- 2.上下界剪枝
-
\[R\in [u,min(R_{u+1}-1,\sqrt{n-v})] \]
-
\[H\in [u,min(H_{u+1}-1,\frac{n-v}{R_{u}\times R_{u}})] \]
-
- 3.可行性剪枝(体积和越界)
-
\[v+minv[u] > n \]
-
- 4.最优性剪枝(面积和更差)
-
\[s+mins[u]>ans \]
-
- 最优性剪枝(面积和更差)
-
\[s+\frac{2(n-v)}{R_{u+1}} > ans \]
-
-
为什么要保留两个面积和更差的剪枝?
-
【Powered By Doubao】
-
第4、5个剪枝虽都围绕表面积优化,但二者存在本质差异与互补性,具体原因如下:
1. 原理不同,覆盖不同逻辑分支
- 第4个剪枝:基于预处理的固定值
mins[u](前u层最小侧面积和,每层取半径、高度为层号时的侧面积累加)。它是一种“静态通用下限”,只要当前表面积s + mins[u] > ans,就说明即使剩余层取理论最小侧面积,总表面积仍超最优解,直接剪枝。 - 第5个剪枝:通过剩余体积
n - v动态推导侧面积下限,结合半径关系(如R_{u+1})。它是“动态实时下限”,利用剩余体积的分配逻辑,推导出侧面积必然超标的情况,剪枝与剩余体积强相关的无效分支。
2. 场景互补,提升剪枝全面性
- 第4个剪枝:处理“仅侧面积部分就已超最优解”的通用场景,不依赖剩余体积的具体数值,通过预处理数组快速判断。
- 第5个剪枝:处理“因剩余体积分配导致侧面积超标”的特殊场景,利用体积与半径的数学关系,覆盖第4个剪枝未涉及的逻辑。
3. 效率互补,减少无效计算
- 单独使用第4个剪枝,无法利用剩余体积的动态信息,可能遗漏与体积相关的无效分支;单独使用第5个剪枝,缺少对通用最小侧面积的快速判断。
- 两者结合,从“固定预处理下限”和“动态体积推导下限”两个维度,更全面地过滤无效搜索路径,大幅减少DFS的计算量,提升算法效率。
Answer
#include <bits/stdc++.h>
using namespace std;
const int Inf = 1e9;
int minv[30],mins[20],n,m;
int ans = Inf;
void dfs(int u,int r,int h,int v,int s){if(u == 0){if(s < ans and v == n) ans = s;return ;}if(v+minv[u] > n) return;if(s+mins[u]>=ans) return;if(s+2*(n-v)/r >= ans) return;for(int i = min(r-1,(int)sqrt(n-v));i >= u;i--){for(int j = min(h-1,(n-v)/(i*i));j >= u;j--){dfs(u-1,i,j,v+i*i*j,s+2*i*j+(u==m?i*i:0));}}
}
int main(){cin>>n>>m;for(int i = 1;i <= m;i++){mins[i] = mins[i-1]+2*i*i;minv[i] = minv[i-1]+i*i*i;}dfs(m,Inf,Inf,0,0);//从下向上遍历if(ans == Inf) puts("0");else cout<<ans<<endl;
}