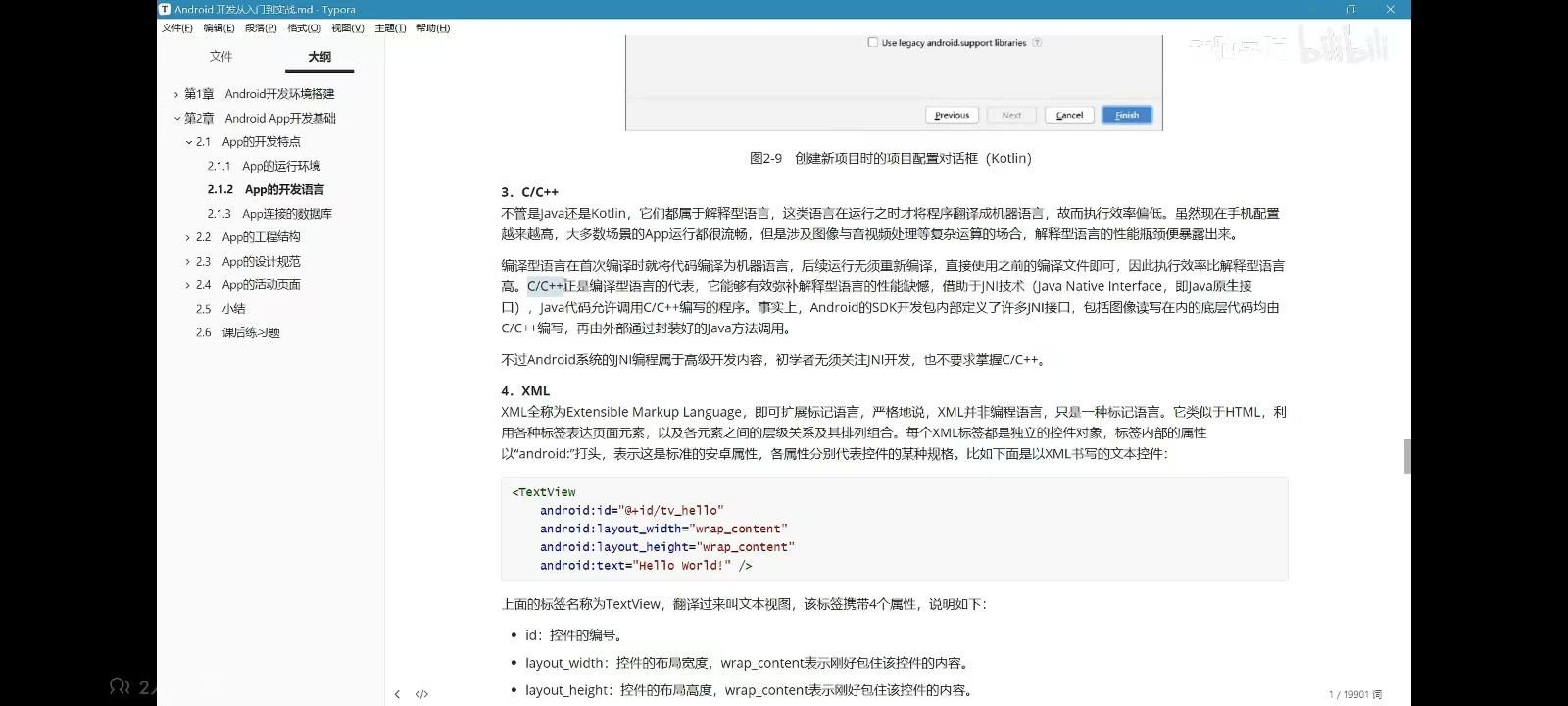
牛顿迭代法(\(Newton's Method\))
快速求零点
对于一条曲线,我们要求它的零点。
先猜测一个零点,再求出该点处的切线,然后取切线的零点重复以上过程,可以快速逼近零点。
快速求函数
我们已知\(G(F(x))=0\),求\(F(x)\)。
先猜测一个函数\(F_0(x)\),套用求零点的过程,可以得到\(F_1(x)=F_0(x)-\frac{G(F_0(x))}{G'(F_0(x))}\),再不断重复提高精度。
正确性证明:
最开始手动求出\([x^0]F(x)\),记作\(F_0(x)\)。
假设现在已知\(F_k(x)\equiv F(x)\pmod{x^n}\)
我们把\(G(F(x))\)在\(F_k(x)\)处泰勒展开得到:
\[G(F(x))=\sum\limits_{i\ge 0}\frac{G^{(i)}(F_k(x))}{i!}(F(x)-F_k(x))^i=0
\]
注意到\(F(x)-F_k(x)\)的次数至少为\(n\),所以:
\[\forall_{i\ge 2}(F(x)-F_k(x))^i\equiv 0\pmod{x^{2n}}
\]
所以\(\sum\limits_{i=0}^1\frac{G^{(i)}(F_k(x))}{i!}(F(x)-F_k(x))^i\equiv 0\pmod{x^{2n}}\)
即:
\[G(F_k(x))+G'(F_k(x))(F(x)-F_k(x))\equiv 0\pmod{x^{2n}}
\]
整理后得到:
\[F(x)\equiv F_k(x)-\frac{G(F_k(x))}{G'(F_k(x))}\pmod{x^{2n}}
\]
我们令\(F_{k+1}(x)\equiv F_k(x)-\frac{G(F_k(x))}{G'(F_k(x))}\pmod{x^{2n}}\),就可以开始倍增求\(F(x)\)了。